信号与系统分析2022春季作业-参考答案：第二次作业

Posted 2022-04-21 卓晴

 

  封面动图来自于： SHUTTERSTOCK网站

 

§00 作业题目

---

  作业要求链接： 信号与系统 2022 春季学期第二次作业 : https://zhuoqing.blog.csdn.net/article/details/123258268

 

§01 参考答案

---

1.1 信号奇偶分解

（1）第一小题

  求解

• 偶分量：

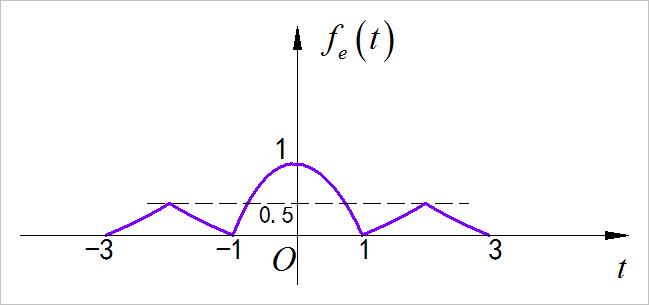
▲ 图1.1.1 信号的偶分量

• 奇分量：

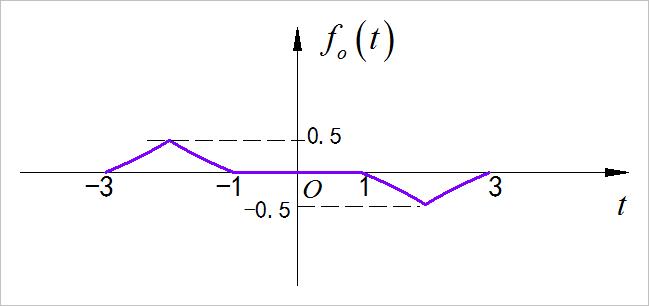
▲ 图 信号的奇分量

（2）第二小题

  求解：

• 偶分量：

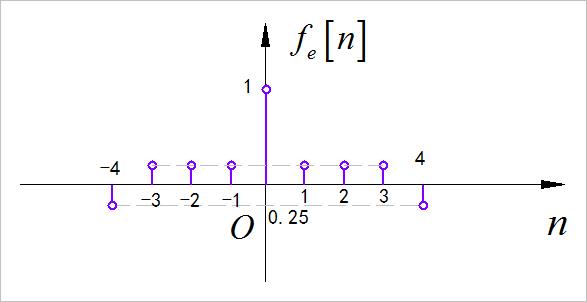
▲ 图1.1.3 信号的偶分量

• 奇分量：

▲ 图1.1.4 信号的奇分量

（3）第三小题

  求解：

• 偶分量：
  

  ▲ 图1.1.5 信号的偶分量

• 奇分量：

▲ 图1.1.6 信号的奇分量

（4）第四小题

  求解：

• 偶分量：

▲ 图1.1.7 信号的偶分量

• 奇分量：
  ▲ 图1.1.8 信号的奇分量

1.2 奇偶分解反问题

1.2.1 必做题

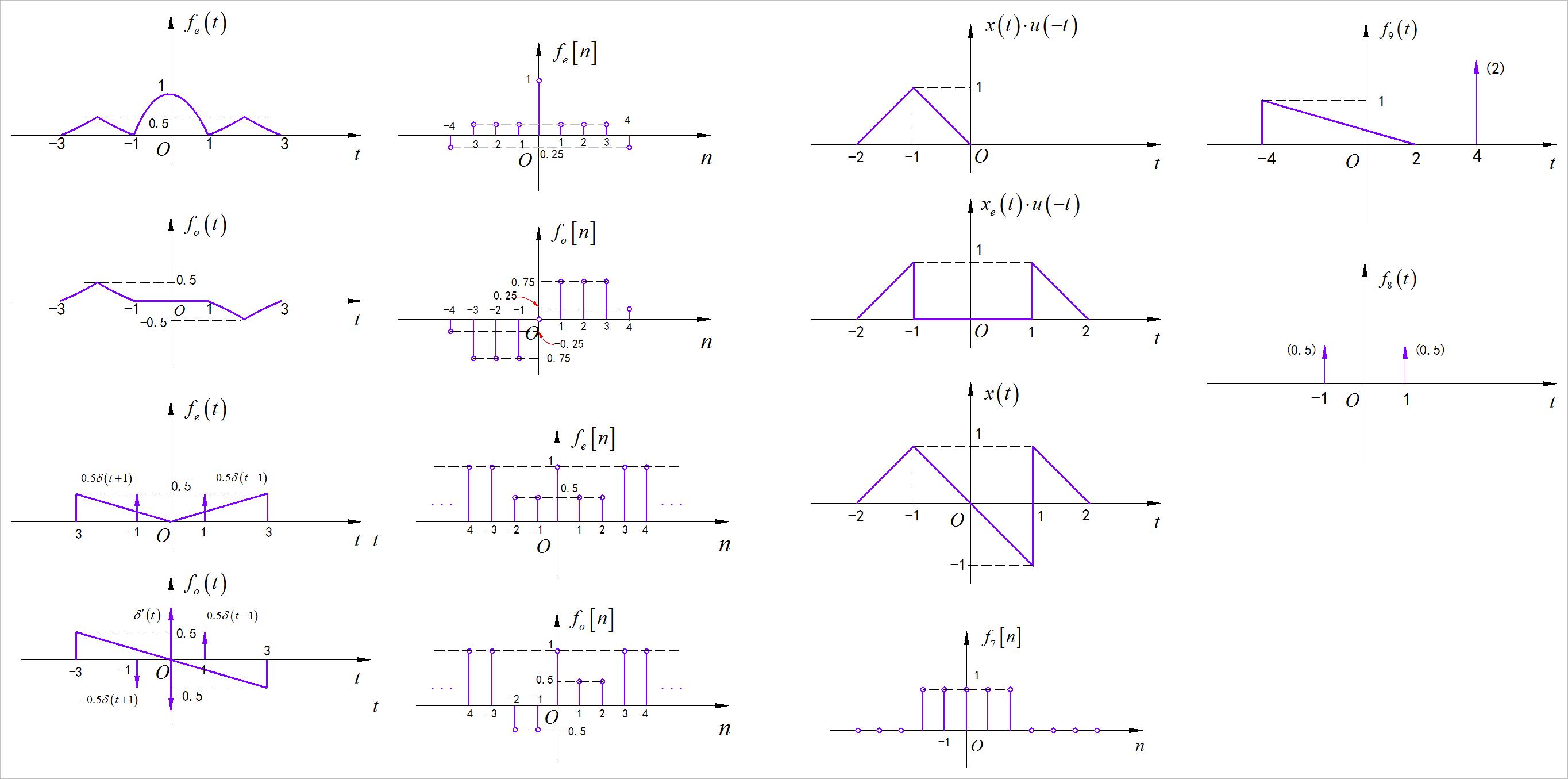
  求解： 根据 $x\left(t+1\right)\cdot u\left(-t-1\right)$ 的波形，往左平移1，获得 $x\left(t\right)\cdot u\left(-t\right)$ 的波形。

▲ 图1.2.1 获得信号左边边的波形

  将上述波形与 $x_o\left(t\right)$ 左边（ $t<0$ ）波形相减，得到波形偶分量左边波形：

$$\left[x\left(t\right)-x_o\left(t\right)\right]\cdot u\left(t\right)=x_e\left(t\right)\cdot u\left(t\right)$$

▲ 图1.2.2 波形偶分量的 左边波形

  根据偶分量是关于y轴左右对称，所以可以绘制出信号的偶分量：

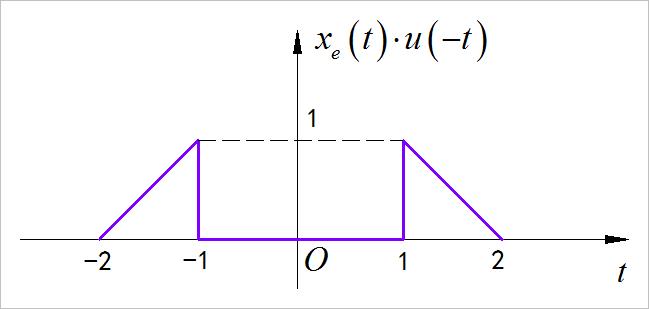
▲ 图1.2.3 信号的偶分量

  将信号的偶分量与奇分量叠加，可以获得信号的波形，如下：

▲ 图1.2.4 信号本身波形

1.3 信号自变量变化

（1）第一小题

  求解：

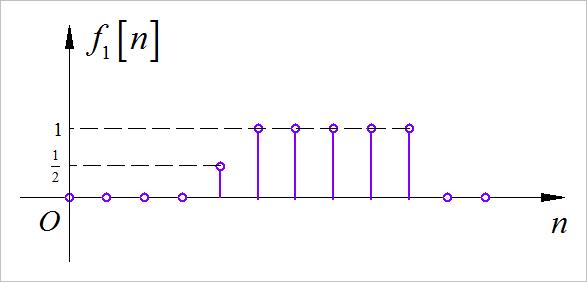
（2）第二小题

  求解：

（3）第三小题

  求解：

（4）第四小题

  求解：

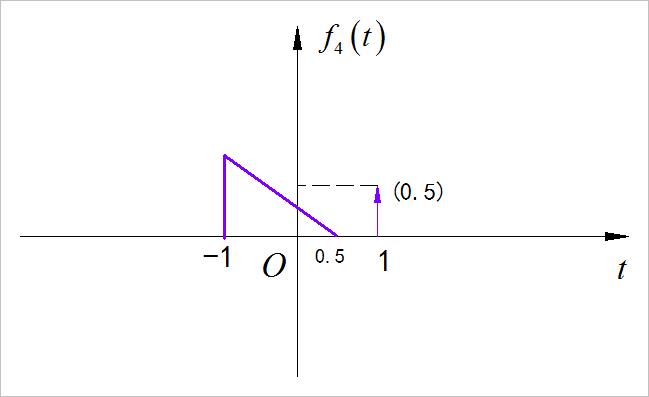
（5）第五小题

  求解：

（6）第六小题

  求解：

（7）第七小题

  求解：

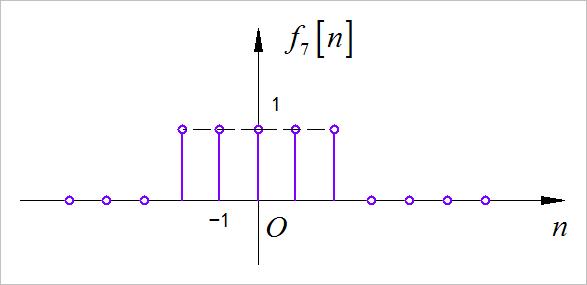
（8）第八小题

  求解：

  由于 $t^2>0$ 所以本题中函数只包含有原来函数在 $t\ge 0$ 的部分，也就是 $\delta \left(t-1\right)$ 。

  根据 $t^2=1$ 的根据有 $\pm 1$ ，所以在 $t=\pm 1$ 处都存在冲激信号。

由于现在面临的信号实际上是一个复合函数， $f_8\left(t\right)=\delta \left[g\left(t\right)-1\right]=\delta \left(t^2-1\right)$ ，所以根据 狄拉克函数 复合函数特性， $$\delta \left[g\left(x\right)\right]=\sum \frac{\delta \left(x-x_i\right)}{\left|g^{\prime }\left(x_i\right)\right|}$$

  所以，对应的两个冲激函数为 $$\frac{1}{2}\delta \left(t\pm 1\right)$$ ，对应的函数图像为

（9）第九小题

  求解：

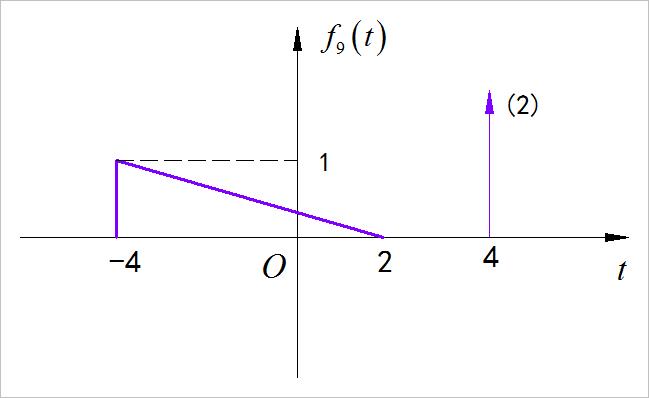
1.4 从系统框图到方程

（1）第一小题

  求解： 根据系统框图综合器，可知 $$x\left(t\right)-y\left(t\right)-4y^{\prime }\left(t\right)=y^{\prime \prime }\left(t\right)$$ 因此 $$y^{\prime \prime }\left(t\right)+4y^{\prime }\left(t\right)+y$$

信号与系统分析2022春季作业-参考答案：第五次作业

信号与系统分析2022春季作业-参考答案：第十次作业

2021年春季学期-信号与系统-第十二次作业参考答案

信号与系统分析2022春季作业-参考答案：第四次作业-第一部分

信号与系统分析2022春季作业-参考答案：第三次作业-第二部分