SS-CA-APPLE：如何对复变函数进行积分？
Posted 卓晴
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了SS-CA-APPLE：如何对复变函数进行积分？相关的知识，希望对你有一定的参考价值。
§01 数学原理
1.1 复变函数积分
1.1.1 曲线的方向
设 C C C 是平面上的光滑（或者按段光滑）曲线。设曲线有两个端点 A , B A,B A,B ，并规定从 A A A 到 B B B 的方向为 C C C 的正方向，那么从 B B B 到 A A A 就是 C C C 的负方向，记做 C − C^ - C− 。此时 C , C − C,C^ - C,C− 称为有向曲线。
关于 简单闭曲线 的方向，定义为曲线上点 P P P 顺此方向前进时，曲线内部始终在 P P P 的左方。
在下面曲线方向定义中，红色箭头规定了曲线的方向。对于简单闭曲线方向定义也可以看成是绕着逆时针前进的方向。 下图不简单闭曲线方向定义是相反的方向。
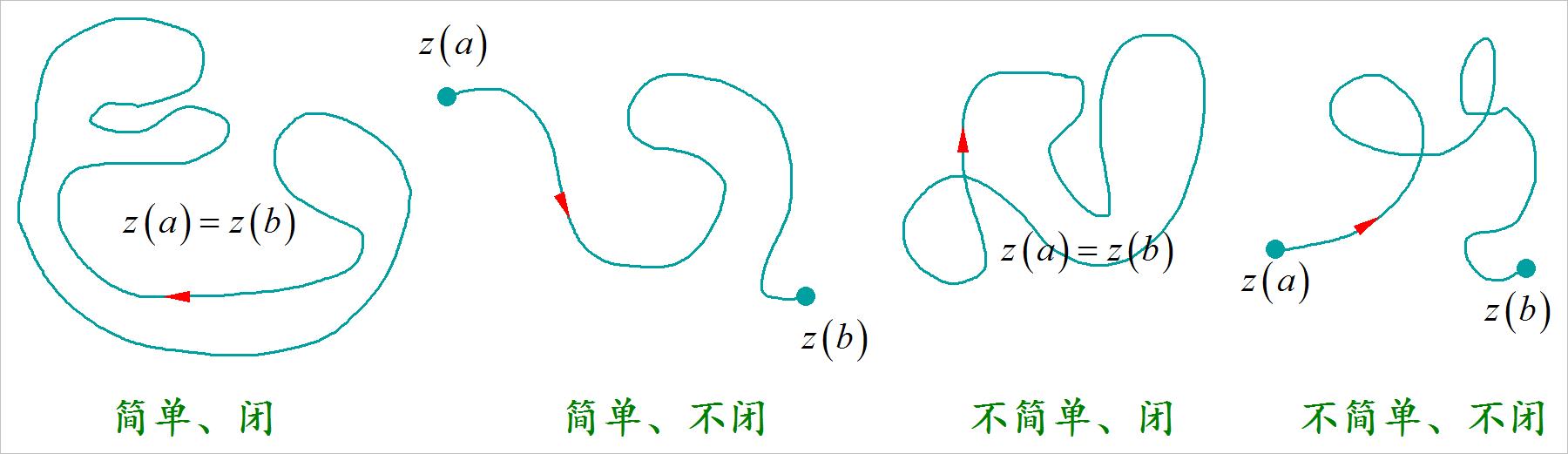
▲ 图1.1.1 。 曲线及其方向定义
1.1.2 沿曲线积分
设函数 w = f ( z ) w = f\\left( z \\right) w=f(z) 定义在区域 D D D 内， C C C 为区域内起点为 A A A ，终点为 B B B 的一条光滑 有向曲线 。把 C C C 人已分成 n n n 个弧段，设分点为 A = z 0 , z 1 , z 2 , ⋯ , z k − 1 , z k , ⋯ , z n = B A = z_0 ,z_1 ,z_2 , \\cdots ,z_k - 1 ,z_k , \\cdots ,z_n = B A=z0,z1,z2,⋯,zk−1,zk,⋯,zn=B 每个弧段 z k − 1 z k ‾ ( k = 1 , 2 , ⋯ n ) \\overline z_k - 1 z_k \\,\\left( k = 1,2, \\cdots n \\right) zk−1zk(k=1,2,⋯n) 上任意取一点 ζ k \\zeta _k ζk ，并作和式 S n = ∑ k = 1 n f ( ζ k ) ( z k − z k − 1 ) = ∑ k = 1 n f ( ζ k ) Δ z k S_n = \\sum\\limits_k = 1^n f\\left( \\zeta _k \\right)\\left( z_k - z_k - 1 \\right) = \\sum\\limits_k = 1^n f\\left( \\zeta _k \\right)\\Delta z_k Sn=k=1∑nf(ζk)(zk−zk−1)=k=1∑nf(ζk)Δzk 记 δ = max k ∈ [ 1 , n ] Δ s k \\delta = \\mathop \\max \\limits_k \\in \\left[ 1,n \\right] \\left\\ \\Delta s_k \\right\\ δ=k∈[1,n]maxΔsk 是所有弧段最大长度。当 n n n 无限增加，且 δ → 0 \\delta \\to 0 δ→0 ，如果不论对 C C C 的划分方法以及 ζ k \\zeta _k ζk 的取法如何， S n S_n SS-CA-APPLE：如何把初等函数扩展到复变函数？