同步电机模型的SIMULINK仿真
Posted studyer_domi
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了同步电机模型的SIMULINK仿真相关的知识,希望对你有一定的参考价值。
2.2 坐标变换
坐标变换的目的是简化原有电机模型非线性和多变量等困难,它的基本思路是在保证变换前后的磁动势等效即维持功率不变的情况下,用一组新的方程组来取代原方程组,用一套新的变量来代替原方程组里的旧变量,实现减少变量和简化模型的目的。基于矢量控制方法的永磁同步电机,经过克拉克(Clarke)变换与派克(Park)变换后可将三相静止坐标系下的复杂变量转换成两相旋转坐标系下的直流量,这样,坐标变换后的永磁同步电机数学模型大为简化,不仅减少了电机控制变量的也降低了其控制难度。
(1)克拉克变换
在三相静止坐标系中,往静止绕组A、B、C中分别注入相互对称的三相正弦电流、、,依据安培环路定理,最终能合成一个以同步速旋转的磁动势FS。而若在两相静止坐标系中,让α轴与A轴重合且滞后于β轴900,并在两个静止绕组中注入相位差900的两相交流电流、,根据变换前后磁动势等效原则,如果两相电流产生的磁动势与三相正弦电流产生的磁动势完全等效,那么在同一控制系统中它们所产生的作用也是完全相同的。克拉克变换实现了从三相静止坐标到两相静止坐标之间的变换。
图2-2上述各种空间矢量之间的关系:
图2-2 从ABC坐标系到坐标系变换
参照图2-2在变换前后功率不变的条件下,利用三角函数关系就能得到两个坐标系之间的变换矩阵。此变换称为克拉克变换,它实现了由静止的三相坐标转化为两相坐标,简化了变量,方程关系式如(2-1)所示:
= (2-1)
而反过来,从两相静止坐标系转换成三相静止坐标的变换叫换克拉克逆变换(又称2S/3S变换),其关系式如式(2-2)所示:
= (2-2)
通过Clark变换实现了从三相交流量到两相交流量的转换。三相静止坐标系ABC中的三个交流量,经过克拉克变换后变成了两相静止坐标系中的两个交流量,且α轴与β轴之间相互正交,便于进一步分析。
(2)派克变换
在两相静止坐标系中,依然为时变的正弦量,为了进一步简化模型,使交流电机能获得相似于直流电机的控制方式,我们可以把两相静止坐标系进一步转换为两相旋转坐标系,即用两个旋转的直流量来替换时变的交流量,并保证变换前后磁动势等效。图2-3为坐标变换的示意图。
由图2-3可以发现,两相旋转坐标系的dq轴之间相互垂直,并以同步速度旋转,d轴滞后于α轴θ角。同样可以利用简单的函数关系即可得出坐标变换的对应关系式。从两相静止坐标系到两相旋转坐标系的变换,称为派克变换(2s/2r变换),变换方程如式(2-3)所示:
= (2-3)
而两相静止坐标系到两相旋转坐标系之间的变换,称为派克反变换(2r/2s变换),变换方程式如式(2-4)所示:
= (2-4)
经过两次变换后的电流波形从①到②再到③,实现从交流变量到直流量的变换,如下图2-4所示:
通过图2-4可以发现,经过两次变换后,三相交流电流变量转换成了两相直流量,这样当我们就能够借用直流电机的控制方式对交流电机进行控制,降低了控制难度,同时提高了响应速度。
电机动力学方程为:
|
| (2-4) |
定子电压方程:
(2-8)
磁链方程:
(2-9)
转矩方程:
(2-10)
轴定子电压;轴定子电流;轴定子磁链;
轴定子电感;转子角速度;定子电阻。
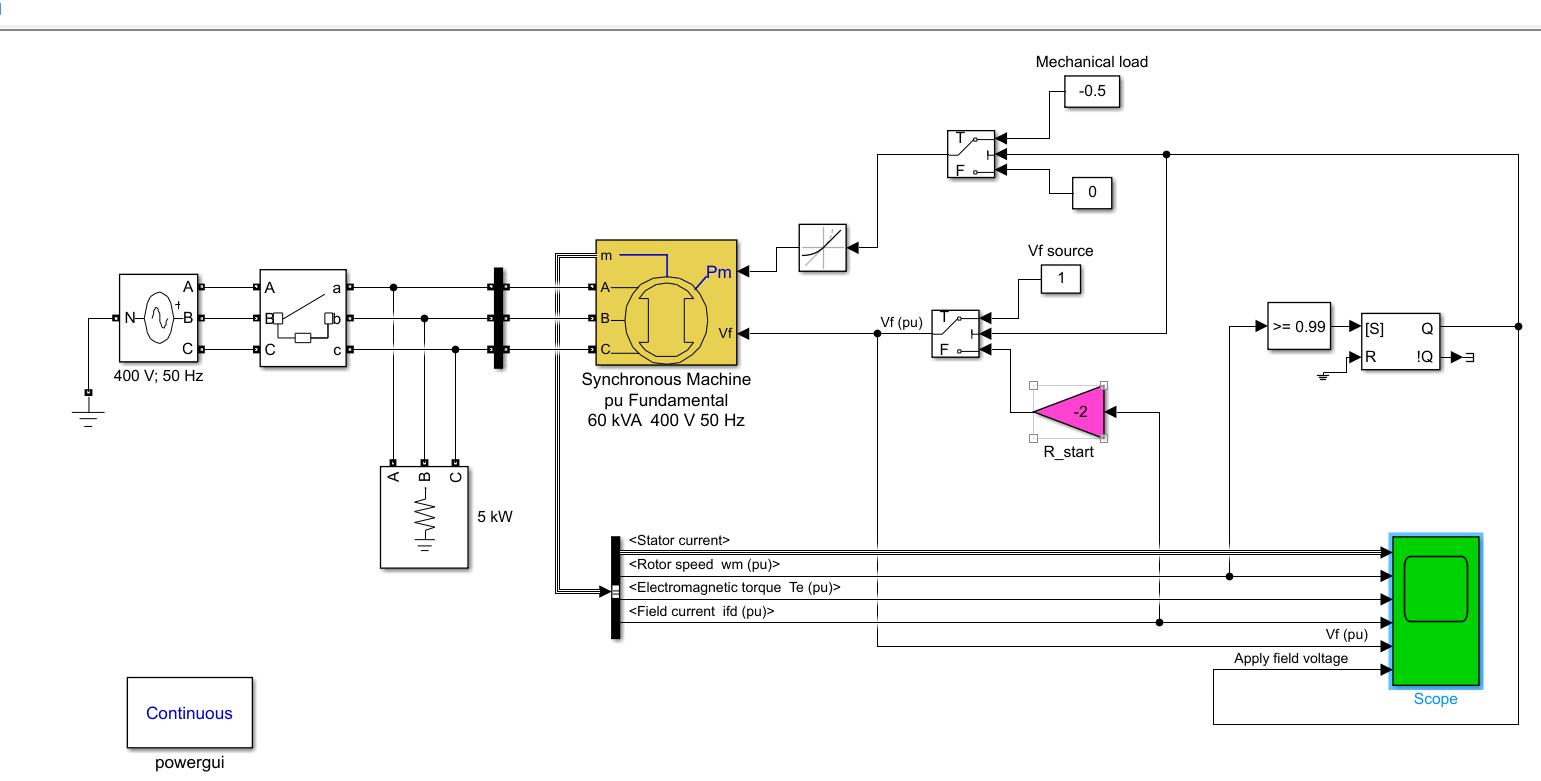
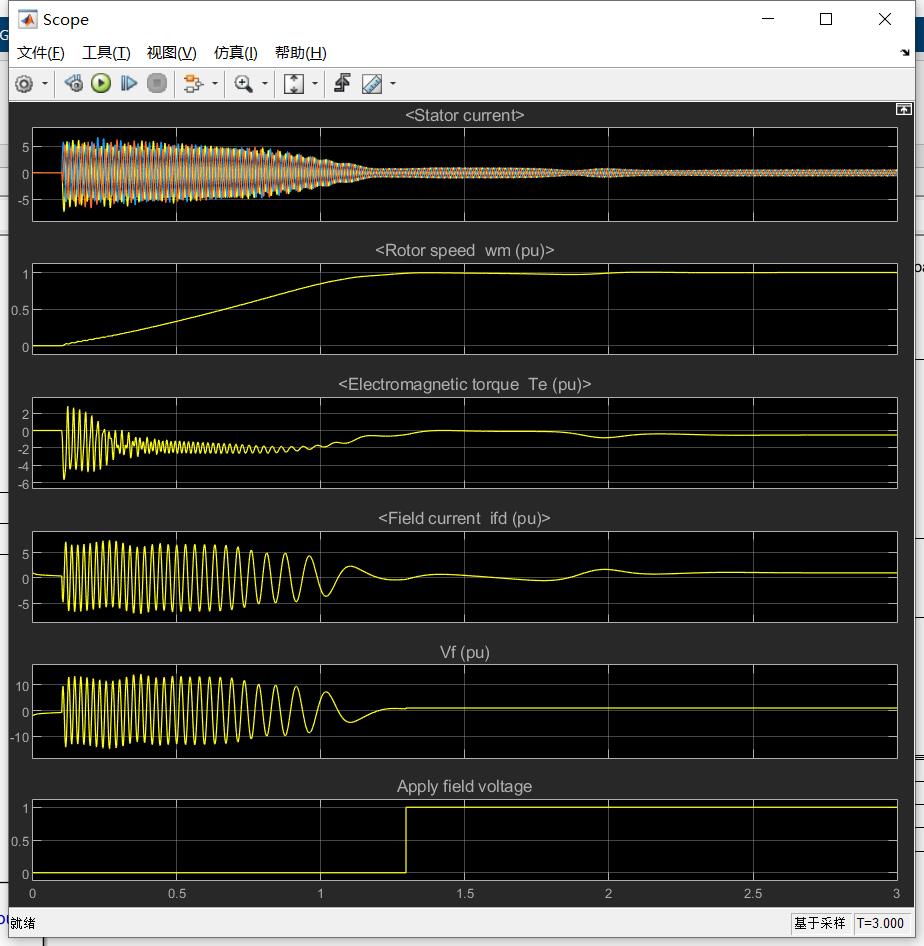

以上是关于同步电机模型的SIMULINK仿真的主要内容,如果未能解决你的问题,请参考以下文章