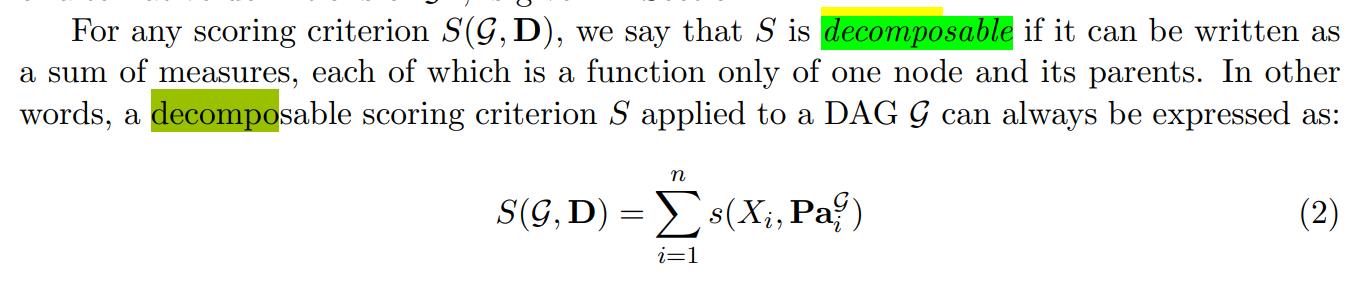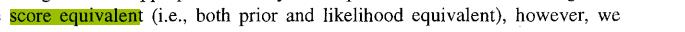论文导读DAG-GNN: DAG Structure Learning with GNN

Posted 2022-04-17 ViviranZ

这也是那篇pianzi的introduction的reference 讲了NOTEARS【也就是文中反复提及的Zheng等人的论文，数学上很basic，如果有时间可以写一下】的一个变种，听起来挺厉害的读一读

摘要

【针对的问题】从联合分布的样本中学习一个可信的（faithful）（DAG） 是一个具有挑战性的组合问题，因为图结点数量的超指数搜索空间的超指数性是难以解决的。

【优化的方法-NOTEARS】最近的一个突破性进展是 将该问题表述为一个具有结构约束的连续优化问题，以确保 acyclicity（Zheng等人，2018）【也就是NOTEARS所解决的的问题】。作者将该方法应用于线性结构方程模型（SEM）和最小二乘损失函数 在统计学上是合理的，但仍然程度有限。

【具体idea：利用深度学习】在深度学习的广泛成功的激励下深度学习能够捕捉复杂的非线性映射。在这项工作中，我们提出了一个深度生成模型，并应用一个变种的结构约束来学习DAG。生成模型的核心是一个变异自动编码器，其参数由一个新的图神经网络架构决定，我们称之为DAG-GNN。

【优势】除了更丰富的容量外，该模型的一个优点是：它能自然地处理离散变量和矢量变量。我们证明，在合成数据集上，所提出的方法对非线性生成的图形学习了更准确的图形；而在具有离散变量的基准数据集上，所学到的图形相当接近于全局最优值。

【源码】The code is available at https:// github.com/fishmoon1234/DAG-GNN.

Introduction

贝叶斯网络（BN）已被广泛用于机器学习应用中（Spirtes等人，1999；Ott等人，2004）。贝叶斯网络的结构采用有向无环图（DAG）的形式，在因果推理中起着至关重要的作用（Pearl，1988），在医学、遗传学、经济学和流行病学中有许多应用。然而其结构学习问题是NP-hard（Chickering等人，2004），并刺激了大量的文献。

基于分数的方法通常将结构学习问题表述为针对未知（加权）邻接矩阵A和观察到的数据样本优化某个分数函数，并有一个组合约束条件，即图必须是无环的。难以解决的搜索空间（复杂度超指数的图形节点数量）给优化带来了巨大挑战。因此，对于规模超过小的实际问题，往往需要采用近似搜索，并附加结构假设（Nie等人，2014；Chow & Liu，1968；Scanagatta等人，2015；Chen等人，2016）。

 最近，Zheng等人（2018）通过使用邻接矩阵的连续函数（特别是A◦A的矩阵指数）制定了一个等价的非周期性约束。这种方法极大地改变了问题的组合性，使其成为一个连续的优化问题，可以通过使用成熟的黑盒求解器来有效解决。然而，这个优化问题是非线性的，因此这些求解器通常只返回一个静止点的解决方案，而不是全局最优。然而，作者表明，根据经验，这种局部解决方案与通过昂贵的组合搜索获得的全局解决方案具有高度的可比性。

随着约束条件的启发式重构，我们重新审视了目标函数。基于分数的目标函数通常对变量和模型类别进行假设。例如，Zheng等人（2018）在线性结构方程模型（SEM）上展示了一个最小二乘法损失。虽然方便，但这种假设往往是有限制的，它们可能无法正确反映现实生活中数据的实际分布。

因此，在深度神经网络（ 这可以说是通用的近似器）的显著成功的激励下，我们在这项工作中开发了一个基于图的深度生成模型，旨在更好地捕捉忠实（faithful）于DAG的采样分布。为此，我们采用了变分推理（Variational Inference）的机制，用专门设计的图神经网络（GNN）对编码器/解码器进行参数化。那么，目标函数（得分）是证据下界（ELBO）。

【ELBO给一个简介，之后可能再写一下变分推理的经典论文导读

变分推断中的ELBO(证据下界)_HFUT_qianyang的博客-CSDN博客_elbo】

与目前蓬勃发展的GNN设计不同（Bruna等，2014；Defferrard等，2016；Li等，2016；Kipf & Welling，2017；Hamilton等，2017；Gilmer等，2017；Chen等，2018；Velickovi ˘c等 ´ ，2018），文中提出的方法是从线性SEM泛化而来，因此，当数据是线性的，新模型至少表现得和线性SEM一样好。【也就是NOTEARS因为假设的是线性结构，所以处理线性问题表现很好】

我们的建议有以下明显的特点和优势。首先，这项工作建立在深度生成模型（特别是变异自动编码器，VAE（Kingma & Welling，2014））的广泛使用上，这些模型能够捕获复杂的数据分布并从中取样。在图的设置下，加权邻接矩阵是一个明确的参数，而不是一个潜在的结构，可与其他神经网络参数一起学习。所提出的网络结构以前还没有被使用过。

第二，VAE的框架自然地处理各种数据类型，特别是不仅有连续的，也有离散的。人们需要做的就是建立与变量性质一致的似然分布（解码器输出）模型。

第三，由于使用图神经网络进行参数化，每个变量（节点）不仅可以是标量值的，而且可以是矢量值的。这些变量被认为是输入/输出到GNNs的节点特征。

第四，我们提出了一个更适合在当前深度学习平台下实施的非周期性约束的变体。Zheng等人（2018）建议的矩阵指数，虽然在数学上很优雅，但可能无法在所有流行的平台上实现或支持自动分化。我们提出了一个多项式的替代方案，在实践中更加方便，并且在数值上与指数一样稳定。我们在由线性和非线性SEM产生的合成数据、离散变量的基准数据集和应用数据集上证明了所提方法的有效性。对于合成数据，提议的DAG-GNN优于Zheng等人（2018）提出的基于线性SEM的算法DAG-NOTEARS。对于基准数据，我们学习到的图与通过使用组合搜索优化贝叶斯信息准则获得的图相比更有优势。

背景和相关工作

一个DAG G和一个联合分布P是相互忠实（faithful）的：如果P中的所有条件独立性有且仅有G所包含的（Pearl，1988）。忠实性条件使人们能够从P中恢复G。如果给定独立同分布D、知道是从一个分布中取出、且这个分布对应于一个忠实但未知的DAG，结构学习（structural learning）指的是从D中恢复DAG。

许多精确和近似的算法用于从数据中学习DAG 的算法，其中包括基于分数和基于约束的方法（Spirtes等人，2000a；Chickering，2002；Koivisto & Sood，2004；Silander & Myllymaki, 2006；Jaakkola等人，2010；Cussens，2011；Yuan & Malone, 2013；Gao & Wei, 2018）。基于分数的方法通常使用一个分数来衡量不同图形对数据的拟合度数据；然后使用搜索程序--如爬坡法（Heckerman等人，1995；Tsamardinos等人，2006。Gmez等人，2011）、前向-后向搜索（Chickering, 2002），动态编程（Singh和Moore，2005；Silander和Myllymaki，2006），A∗（Yuan和Malone，2013）。(Yuan & Malone, 2013)。或整数编程（Jaakkola等人，2010；Cussens, 2011年；Cussens等人，2016年），以找到最佳图形。常用的贝叶斯评分标准，如BDeu和 贝叶斯信息准则（BIC），是可分解的（decomposable）、一致（consistent）、局部一致的（local consistent）（Chickering，2002），以及得分等价的（score equivalent）（Heckerman等人，1995）。

 可分解的保证了我们可以对这个score“分而治之”、consistency保证了越大越好（而不会出现score高了的DAG反而不能更好刻画分布的独立性条件）、local consistency保证对加一条边（locally）的consistency

具体见Chickering, D. M., Heckerman, D., and Meek, C. Large-sample learning of Bayesian networks is NP-hard. Journal of Machine Learning Research, 5:1287–1330, 2004.

一篇很长、有很多证明的论文，读了很久但是很有收获

 这篇更长了…………离谱插个眼之后去看看

 Heckerman, D., Geiger, D., and Chickering, D. M. Learning Bayesian networks: The combination of knowledge and statistical data. Machine learning, 20(3):197–243, 1995.

为了使DAG的搜索空间具有可操作性【否则容易出现NP-难的问题】，近似方法做出了额外的假设，如有界的树宽（Nie等人，2014），树状结构（Chow 和Liu，1968），近似（Scanagatta等人，2015）和 关于DAG的其他约束（Chen等人，2016）。许多 Bootstrap（Friedman等人，1999）和基于抽样的结构学习算法（Madigan等人，1995；Friedman & Koller, 2003; Eaton & Murphy, 2012; Grzegorczyk & Husmeier, 2008; Niinimaki & Koivisto ¨, 2013; Niinimaki 等人，2012；He等人，2016）也被提出来解决昂贵的搜索问题。

相比之下，基于约束的方法使用（条件）独立性测试来测试每个变量对之间是否存在边。变量对之间的存在。流行的算法包括SGS（Spirtes 等人，2000b）、PC（Spirtes等人，2000b）、IC（Pearl, 2003）和FCI（Spirtes等人，1995；Zhang，2008【插眼，之后跟进】）。最近，出现了一套混合算法，结合了基于分数和基于约束的方法，如 MMHC（Tsamardinos等人，2003），并将基于约束的方法应用于多种环境（Mooij等人。2016).

由于NP的困难性，传统的DAG学习方法通常处理离散变量（如上所述）或联合高斯变量（Mohan等人，2012；Mohammadi 等人，2015）。最近，有人提出了一种新的连续优化方法（Zheng等人，2018），它将离散的搜索程序转化为平等的约束条件。这种方法使用一套连续优化技术，如梯度下降技术。该方法实现了良好的结构恢复结果，尽管它为了便于论述，只应用于线性SEM。

神经网络方法仅在很短的时间内开始出现。最近。Kalainathan等人（2018）提出了一种GAN式（生成对抗网络）的方法，即对每个变量应用一个单独的生成模型应用于每个变量，并使用判别器来区分真实和生成样本的联合分布。这种方法似乎可以很好地扩展 很好，但非周期性没有被强制执行。

神经网络的DAG结构学习

我们的方法通过使用一个深度生成模型来学习DAG的加权邻接矩阵，该模型概括了线性SEM，我们以此为起点。

（接下来大量公式且英文较容易，直接上图＋解释）

３.１　线性SEM模型

 首先给了典型线性SEM的模型……很基础不讲

３.２　提出的GNN模型

首先，（２）可以表示为 ，这个式子是深度学习界公认的一般形式，是对参数化图神经网络的抽象，将节点特征Z作为输入，并返回X作为高层表征。几乎所有的图神经网络（Bruna等人，2014；Defferrard等人，2016；Li等人，2016；Kipf & Welling，2017；Hamilton等人，2017；Gilmer等人，2017；Chen等人，2018；Velickovi ˘ c等人 ´ ，2018）都可以写成这种形式。 例如，流行的GCN（Kipf & Welling, 2017）架构读取

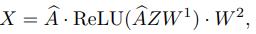
 其中Ab是A的归一化，W1和W2是参数矩阵。

由于特殊的结构（2），我们提出了一个新的GNN架构

参数化函数f1和f2分别对Z和X进行有效的（可能是非线性的）变换。如果f2是可逆的，那么(3)等同于这是线性SEM(1)的一个广义版本。我们将把这些函数的实例化推迟到后面的小节中讨论。其中一个原因是，f2中的激活必须与变量X的类型相匹配，这个问题将与离散变量一起讨论。

３.３利用VAE进行模型学习

 首先（由变分推理的目标可知），我们想找到的p(x)是找不到的，因此我们要用变分贝叶斯，即

 给一个（4）的推断，很简单。

 ELBO适合于变异自动编码器（VAE）（Kingma & Welling, 2014），给定一个样本X^k，编码器（推理模型）将其编码为密度为q（Z|X^k）的潜变量Z；而解码器（生成模型）试图从Z中重建密度为p（X^k |Z）的X^k。这两种密度都可以通过使用神经网络进行参数化。

除去后面要完成的概率规范(Modulo the probability specification)，上一小节中讨论的生成模型（3）扮演了解码器的角色。然后，我们提出相应的编码器:

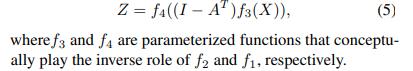
  这段主要是提及ELBO的相关方法，并且根据我们问题的目标公式（３）得到encoder－decoder模型

基础的ELBO的相关知识点，参考上方提到的变分推断中的ELBO(证据下界)_HFUT_qianyang的博客-CSDN博客_elbo

和论文Kingma, D. P. and Welling, M. Auto-encoding variational Bayes. In ICLR, 2014.

一点简单的推导笔记如下：（关键还是看blog这个不太清楚）

 ３.４架构和损失函数

 要用VAE，我们要找到（４）中的分布函数，因为X^ｋ和Z都是ｍ＊ｄ的矩阵。为了简便性我们把先验证明建模为一个标准的正态矩阵：

↑解释factored Gaussian，其实就是独立的

多层感知器（MLP）_西柚kkkkkiven的博客-CSDN博客_多层感知器

↑解释多层感知机……好了我知道我是菜鸡这个还得专门去看看

  （关键是把两个函数f_1,f_4设置为了恒等映射，只利用多层感知器学习另外两个）

人们可以在每个编码器/解码器内切换MLP和恒等映射，但我们发现性能上的竞争力较弱。一个可能的原因是，目前的设计（7）把重点放在线性SEM的样本（I-A^T）^-1Z的非线性变换上，这更好地捕捉了非线性的特点。

我到现在也不知道为什么 ………我猜可能做了一些估计，我先发邮件问问吧。

请注意，在自动编码器框架下，Z被认为是潜在的（而不是线性SEM中的噪声）。因此，Z的列维可能与d不同。从神经网络的角度来看，改变Z的列维只影响到参数矩阵W2和W3的大小。有时，如果观察到数据的内在维度较小，人们可能希望使用一个比d小的数字。

图1显示了结构的说明。

３.５离散变量

【主要问题所在，之后认真看看】

所提方法的一个优点是它能自然地处理离散变量。我们假设每个变量j有有限且基数（cardinality）为d。

因此，我们让X的每一行都是一个one-hot向量，

one-hot向量形式_予亭的博客-CSDN博客_one-hot

我们仍然使用标准的矩阵正态来模拟先验，使用派生高斯来模拟变分后验，（6）是编码器。另一方面，我们需要稍微修改似然，以应对变量的离散性。

具体来说，我们让p(X|Z)是一个具有概率矩阵P_X的派生分类分布（factored categorical distribution），其中每一行是相应分类变量的概率向量。为了实现这一点，我们将f2从身份映射改为逐行的softmax，并将解码器（7）修改为

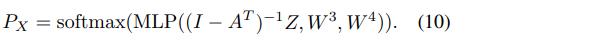
相应地，对于ELBO，KL项（8）保持不变。但重建项（9）需要修改为 

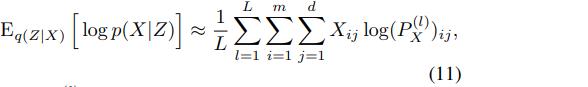
其中P ^(l)_X是解码器（10）的输出，其输入为蒙特卡洛样本Z^(l) ∼ q(Z|X), l=1,...,L. 

3.6 与线性SEM关系

从上面的讨论中可以看出，我们提出的模型是如何从线性SEM发展而来的：我们将非线性应用于SEM的抽样程序（2），将产生的模型作为一个解码器，并与之搭配一个变分编码器来进行可操作的学习。与普通的自动编码器相比，变分版本允许对潜在空间进行建模，并从中生成样本。 

现在，我们以相反的思维流程，来建立Zheng等人（2018）所考虑的线性SEM的损失函数与我们的损失函数之间的联系。我们首先剥去自动编码器的变异成分。这个普通版本使用（5）作为编码器，（3）作为解码器。为了表述清楚，我们把Xb写成解码器的输出，以区别于编码器的输入X。 一个典型的（最小化的）loss函数是：

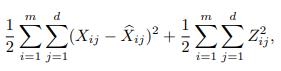
其中第一项是重建误差，第二项是潜在空间的正则化。人们认识到，如果标准差SX为1，均值MX为Xb，并且只从变异后验中抽取一个蒙特卡洛样本，则重建误差与ELBO中的负重建精度（negative reconstruction accuracy）（9）相同，最多差一个常数。此外，如果标准差SZ为1，均值MZ为Z，则正则项与ELBO中的KL散度相同。

如果我们进一步剥离（可能是非线性的）映射f1和f4，那么编码器（5）和解码器（3）分别读取Z=（I - AT ）X和Xb=（I - AT ）-1Z。这一对的结果是完美的重建，因此，样本损失减少到

这是Zheng等人(2018)使用的最小二乘法损失，也是合理的。

3.7 非环约束

无论是最大化ELBO（4）还是最小化最小二乘法损失（12）都不能保证得到的A的相应图是无环的。Zheng等人（2018）将损失函数与一个平等约束配对，该约束的满足确保了非环性。

这个想法基于这样一个事实：非负邻接矩阵B的k次方的（i，j）元素的正性表明节点i和j之间存在一条长度为k的路径，因此，Bk的对角线的正性揭示了循环。作者利用了一个技巧，即矩阵指数允许有一个泰勒级数（因为它在复平面上是解析的），这只不过是矩阵的所有非负整数幂的加权和。zeorth幂的系数（身份矩阵Im×m）是1，因此对于DAG来说，B的指数的迹必须正好是m。为了满足非负性，我们可以让B是A的元素平方，即B=A ◦A。

都是NOTEARS上的内容 略

3.8 Training

 基于以上所述，学习问题为

 其中未知数包括矩阵A和所有 的所有参数θ（目前我们有θ = W1 , W2 , W3 , W4). 非线性平等约束问题已被充分研究。问题已被充分研究，我们使用增强的拉格朗日方法来解决它。为了完整起见，我们在这里总结一下算法；读者可以参考标准的 教科书，如Bertsekas(1999)的第4.2节，以了解细节和收敛分析。

定义增广的拉格朗日函数

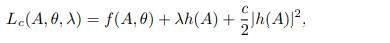
其中λ是拉格朗日乘数，c是惩罚参数。当c=+∞时，Lc（A，θ，λ）的最小化器必须满足h（A）=0，在这种情况下，Lc（A，θ，λ）等于目标函数f（A，θ）。因此，策略是逐步增加c，对于每一个c来说，最小化无约束的增强拉格朗日。 拉格朗日乘数λ也相应地被更新，使其收敛到最优条件下的乘数。

存在一些更新λ和增加c的变体，但一个典型的有效规则是这样的：

 其中η>1和γ<1是调整参数。我们发现，通常η=10和γ=1/4效果很好。子问题（14）可以通过使用黑盒随机优化求解器来解决，注意ELBO是在一组样本上定义的。

4 实验

在本节中，我们提出了一套全面的实验来证明所提出的方法DAG-GNN的有效性。在第4.1节中，我们与Zheng等人（2018）提出的基于线性SEM的方法DAG-NOTEARS在由抽样广义线性模型产生的合成数据集上进行比较，重点是非线性数据和矢量值数据（d>1）。在第4.2节中，我们展示了我们的模型在离散数据方面的能力，这些数据经常出现在具有评估质量的基础真相的基准数据集中。为了进一步说明所提出的方法的有用性，在第4.3节中，我们将DAG-GNN应用于一个蛋白质数据集，用于发现一致的蛋白质信号网络，以及一个知识库数据集，用于学习因果关系。
我们的实现是基于PyTorch（Paszke等人，2017）。我们使用Adam（Kingma & Ba, 2015）来解决子问题（14）。为了避免过度参数化，我们将变异后验q(Z|X)参数化为具有恒定单位方差的派生高斯，同样，对于似然p(X|Z)也是如此。当提取DAG时，我们使用阈值0.3，遵循Zheng等人（2018）的建议。对于基准和应用数据集，我们在目标函数中包括A的Huber-norm正则化，以鼓励更快速的收敛。

4.1合成数据集

合成数据集是以如下方式产生的。我们首先使用预期节点度为3的Erdos-Renyi模型生成一个随机的DAG，然后为边分配统一的随机权重，得到加权的邻接矩阵A。通过对（广义）线性模型进行抽样，产生一个样本X，其函数g即将阐述。噪声Z遵循标准的矩阵正态。当维度d=1时，我们用小写字母表示向量；即x=g(AT x)+z。我们将DAG-GNN与DAG-NOTEARS进行比较，并报告structural Hamming distance（SHD）和false discovery rate（FDR），每个都是五个随机重复的平均数。在样本量n=5000的情况下，我们在四种图的大小m∈10, 20, 50, 100上进行了实验。在第4.1.1和4.1.2节中，我们考虑标量值变量（d=1），在第4.1.3节中考虑矢量值变量（d>1）。 

 4.1.1 线性情况

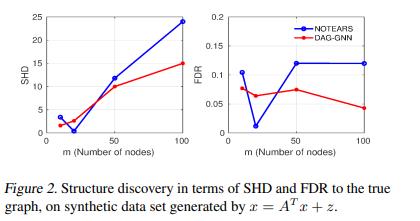
这种情况是线性SEM模型，g是恒等映射。SHD和FDR绘制在图2中。我们可以看到，当图形较大时，用所提方法学习的图形比用DAG-NOTEARS学习的图形要准确得多。

4.1.2非线性情况 

我们现在考虑由以下模型产生的数据

对于一些非线性函数h.采取一阶近似（忽略x的高阶项），可以得到图邻接矩阵的修正近似h‘(0) A。这个近似的基本事实保持了DAG的结构，只是对边缘权重进行了缩放。

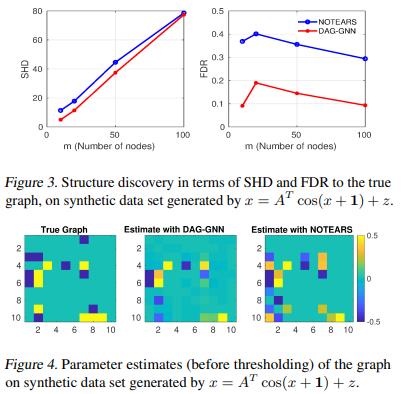
我们取h(x)=cos(x+1)，并在图3中画出SHD和FDR。我们观察到DAG-GNN在SHD方面比DAG-NOTEARS略有改善。此外，FDR也有很大的提高，大约为3倍，这表明DAG-GNN在选择正确的边上更准确。这一观察结果与图4中显示的参数估计值一致，其中基本事实（ground truth）被设定为- sin(1)A。热图证实了DAG-GNN导致了更少的 "误报"，并恢复了一个相对更稀疏的矩阵。

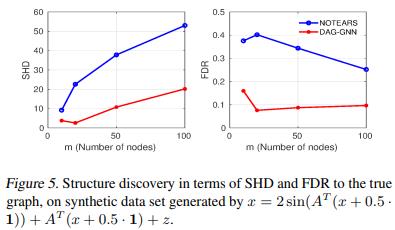
我们进一步试验了一个更复杂的非线性生成模型，其中非线性发生在变量的线性组合之后，而前面的情况是在线性组合之前对变量施加非线性。具体来说，我们考虑

 并将结果绘制在图5中。我们可以看到，在较高的非线性的情况下，所提出的方法在SHD和FDR方面明显优于DAG-NOTEARS的结果。

 

 4.1.3 向量的情形

我们提出的方法提供了一个建模的好处，即变量可以是d>1的矢量值。此外，由于Z位于自动编码器的潜在空间，而不是像线性SEM那样被解释为噪声，（因此）如果他/她认为变量有较低维度，可以采取较小的列维d_Z < d。为了证明这种能力，我们构建了一个数据集，其中不同的维度来自于线性SEM的随机缩放和扰动的样本。具体来说，给定一个图形邻接矩阵A，我们首先从线性SEM中构建一个样本x˜∈R^m×1: 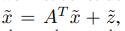，然后生成第k个维度，其中u^k和v^k是标准正态的随机标量，z^k是一个标准正态向量。最终的样本是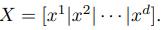 

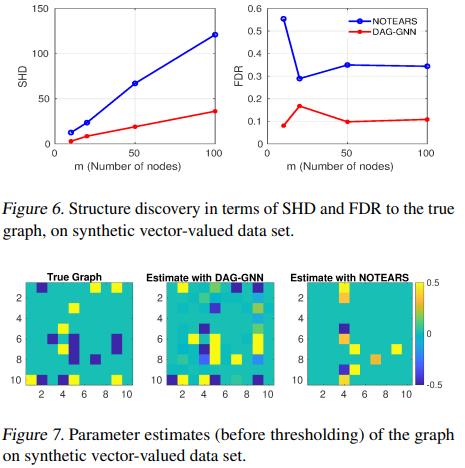
我们让d = 5，d_Z = 1，并比较DAG-GNN和DAG-NOTEARS。SHD和FDR被绘制在图6中。该图清楚地显示了所提方法的性能明显更好。此外，参数估计值显示在图7中，与ground truth A相比较。我们可以看到，DAG-GNN的估计图成功地捕获了所有的ground truth edges，估计的权重也很相似。另一方面，DAG-NOTEARS几乎没有学习到图的内容。

 

 4.2 基准数据集

所提议的方法的一个好处是，它可以自然地处理离散变量，这是线性SEM所不允许的情况。我们在三个离散的基准数据集上演示了DAG-GNN的使用：Child, Alarm, and Pigs (Tsamardinos et al., 2006). 用于比较的是最先进的精确DAG求解器GOPNILP（Cussens等人，2016），它是基于一个受限的整数编程公式。我们使用1000个样本进行学习。

从表1可以看出，我们的结果相当接近基本事实，而GOPNILP的结果几乎是最优的，这并不令人惊讶。DAG-GNN表现出的BIC分数差距可能是由相对简单的自动编码器结构造成的，它在逼近多叉分布方面不太成功。然而，令人鼓舞的是，所提出的方法作为一个统一的框架可以处理离散变量，只需在网络结构上稍作改变。

 4.3 实际应用

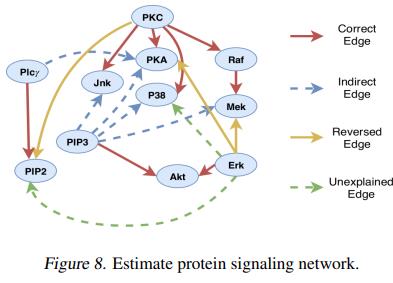
我们考虑了一个生物信息学数据集（Sachs等人，2005）。发现一个基于蛋白质和磷脂表达水平的蛋白质信号网络。这是 一个广泛用于研究图形模型的数据集。实验注释被生物研究界接受。该数据集提供了对人类免疫系统中多种磷酸化蛋白和磷脂成分的表达水平的连续测量。而建模的网络则提供了通路成分之间的排序 路径成分之间的联系。基于 n=7466个样本，m=11种细胞类型，Sachs等人（2005年） 估计图中有20条边。

在表2中，我们将DAG-GNN与DAG-NOTEARS 以及FSG，即Ramsey等人（2017）提出的快速贪婪搜索方法，与Sachs等人（2017）提供的Ground truth进行比较。我们提出的方法实现了 最低的SHD。我们在图8中进一步展示了我们的估计 图。我们注意到，它是一个无环的。我们的方法成功地学习了20条真实的边缘中的8条（如图所示 红色箭头），并预测出5条间接连接的边（蓝色 虚线箭头）以及3条反向边（黄色箭头）。

在另一个应用中，我们对知识库模式中定义的关系开发了一个新的因果推理任务。该任务旨在学习一个BN，其中的节点是关系，边表示一个关系是否暗示另一个关系。例如，人/国籍的关系可能暗示人/语言，因为一个人的口头语言自然与他/她的国籍相关联。这项任务具有实用价值，因为大多数现有的知识库都是由手工构建的。这项任务的成功有助于为新的实体提出有意义的关系，并减少人类的努力。我们从FB15K-237（Toutanova等人，2015）构建了一个数据集，并在表3中列出了一些提取的因果关系。由于篇幅限制，我们将细节和更多结果推迟到补充材料中。人们看到，这些结果是相当直观的。我们计划与现场专家进行全面研究，以系统地评估提取结果。 

5.结论 

DAG结构学习是一个具有挑战性的问题，在图形模型的文献中被长期追求。这种困难在很大程度上是由于组合式表述中所产生的NP困难性。Zheng等人（2018）提出了一个等价的连续约束，为使用发达的连续优化技术来解决该问题提供了机会。在这种情况下，我们探索了神经网络作为功能近似器的力量，并开发了一个深度生成模型来捕捉复杂的数据分布，旨在通过不同的目标函数设计更好地恢复底层DAG。特别是，我们采用了变分自动编码器的机制，并用新的图形神经网络架构对其进行参数化。所提出的方法不仅可以处理由超越线性的参数模型产生的数据，还可以处理一般形式的变量，包括标量/矢量值和连续/离散类型。我们在合成、基准和应用数据上进行了广泛的实验，证明了该提议的实际竞争力

好了我要去看代码了，CU~