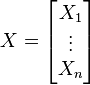协方差与自相关
Posted 麦好
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了协方差与自相关相关的知识,希望对你有一定的参考价值。
协方差矩阵是一个矩阵,其每个元素是各个向量元素之间的协方差。这是从标量随机变量到高维度随机向量的自然推广。
假设 是以
是以 个标量随机变量组成的列向量,
个标量随机变量组成的列向量,
并且 是其第i个元素的期望值,即,
是其第i个元素的期望值,即, 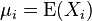 。协方差矩阵被定义的第i,j项是如下:
。协方差矩阵被定义的第i,j项是如下:
即:
-
-
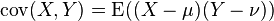 ,
,
-
 ,
,
-
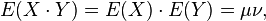
-
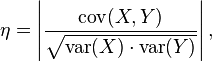
-
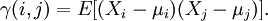
-

-

-
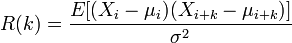
-
 ......... 期望值。
......... 期望值。
-
 ........ 在t(i)时的随机变量值。
........ 在t(i)时的随机变量值。
-
 ........ 在t(i)时的预期值。
........ 在t(i)时的预期值。
-
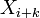 .... 在t(i+k)时的随机变量值。
.... 在t(i+k)时的随机变量值。
-
 .... 在t(i+k)时的预期值。
.... 在t(i+k)时的预期值。
-
 ......... 为方差。
......... 为方差。
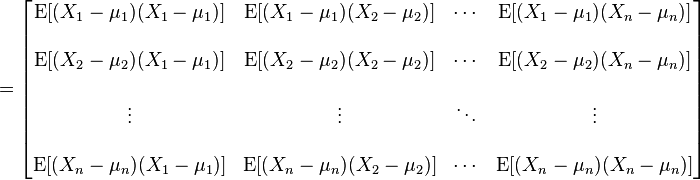
期望值分别为
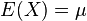 与
与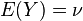 的两个实数随机变量X 与Y 之间的协方差定义为:
的两个实数随机变量X 与Y 之间的协方差定义为:其中E是期望值。它也可以表示为:
如果X 与Y 是统计独立的,那么二者之间的协方差就是0,这是因为
但是反过来并不成立,即如果X 与Y 的协方差为0,二者并不一定是统计独立的。
取决于协方差的相关性η
更准确地说是线性相关性,是一个衡量线性独立的无量纲数,其取值在[0,+1]之间。相关性η = 1时称为“完全线性相关”,此时将Yi对Xi作Y-X 散点图,将得到一组精确排列在直线上的点;相关性数值介于0到1之间时,其越接近1表明线性相关性越好,作散点图得到的点的排布越接近一条直线。
在统计学中,特定时间序列或者连续信号 Xt 的自协方差是信号与其经过时间平移的信号之间的协方差。如果序列的每个状态都有一个平均数 E[Xt] = μt,那么自协方差为
其中 E 是期望值运算符。如果 Xt 是二阶平稳过程,那么有更加常见的定义:
其中 k 是信号移动的量值,通常称为延时。如果用方差 σ2 进行归一化处理,那么自协方差就变成了自相关系数R(k),即
需要注意的是,在有些学科中自协方差术语等同于自相关。
将一个有序的随机变量系列与其自身相比较,这就是自相关函数在统计学中的定义。每个不存在相位差的系列,都与其自身相似,即在此情况下,自相关函数值最大。如果系列中的组成部分相互之间存在相关性(不再是随机的),则由以下相关值方程所计算的值不再为零,这样的组成部分为自相关。
所得的自相关值R的取值范围为[-1,1],1为最大正相关值,-1则为最大负相关值,0为不相关。
-
以上是关于协方差与自相关的主要内容,如果未能解决你的问题,请参考以下文章