MATLAB定态氢原子波函数可视化
Posted slandarer
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了MATLAB定态氢原子波函数可视化相关的知识，希望对你有一定的参考价值。
在知乎看到了
[王欢]的[用 Python+SciPy 可视化定态氢原子波函数（一）]
[王大可]的[利用Mathematica将定态氢原子波函数可视化]
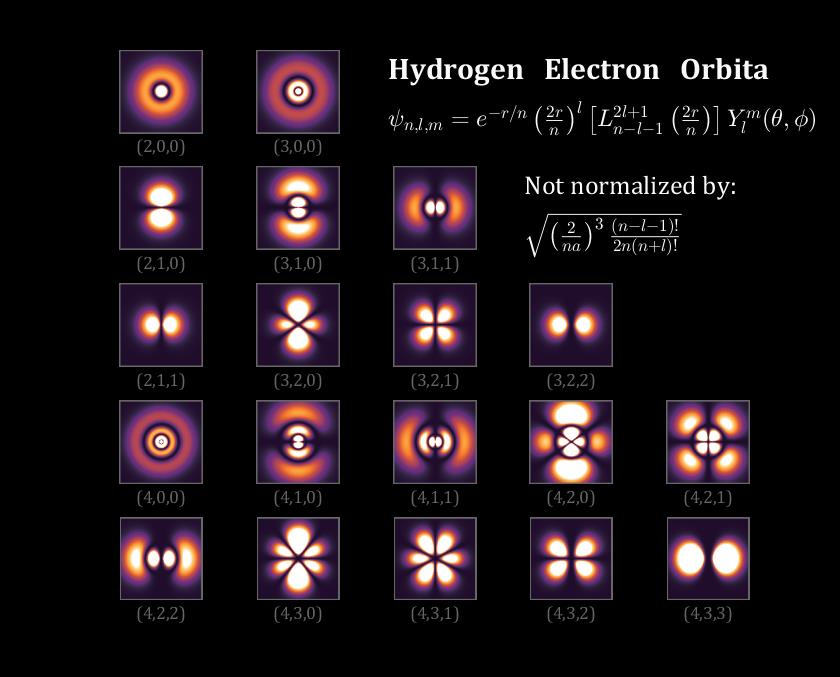
手痒，想用MATLAB也实现一下，David Griffiths 所著的 Introduction to Quantum Mechanics 中:
ψ
n
,
l
,
m
(
r
,
θ
,
ϕ
)
=
R
n
l
(
r
)
Y
l
m
(
θ
,
ϕ
)
\\psi_n, l, m(r,\\theta, \\phi)=R_nl(r)Y_l^m(\\theta, \\phi)
ψn,l,m(r,θ,ϕ)=Rnl(r)Ylm(θ,ϕ)
即，函数由径向波函数及球形谐函数两部分组成，展开一下径向波函数是这样的：
ψ
n
,
l
,
m
(
r
,
θ
,
ϕ
)
=
(
2
n
a
)
3
(
n
−
l
−
1
)
!
2
n
(
n
+
l
)
!
e
−
r
/
n
a
(
2
r
n
a
)
l
[
L
n
−
l
−
1
2
l
+
1
(
2
r
n
a
)
]
Y
l
m
(
θ
,
ϕ
)
\\psi_n, l, m(r,\\theta, \\phi)=\\sqrt\\left(\\frac2n a\\right)^3 \\frac(n-l-1) !2 n(n+l) ! e^-r / n a\\left(\\frac2 rn a\\right)^l\\left[L_n-l-1^2 l+1\\left(\\frac2 rn a\\right)\\right] Y_l^m(\\theta, \\phi)
ψn,l,m(r,θ,ϕ)=(na2)32n(n+l)!(n−l−1)!e−r/na(na2r)l[Ln−l−12l+1(na2r)]Ylm(θ,ϕ)
其中 a a a 为玻尔半径，数值约为5.2917721092(17)×10^-11米，本文仅做可视化，方便起见，将 a a a 数值设置为1，并省略归一化系数，因此我们实际上本文绘制的是如下函数的图像：
ψ n , l , m ( r , θ , ϕ ) = e − r / n ( 2 r n ) l [ L n − l − 1 2 l + 1 ( 2 r n ) ] Y l m ( θ , ϕ ) \\psi_n, l, m(r,\\theta, \\phi)=e^-r / n\\left(\\frac2 rn\\right)^l\\left[L_n-l-1^2 l+1\\left(\\frac2 rn\\right)\\right] Y_l^m(\\theta, \\phi) ψn,l,m(r,θ,ϕ)=e−r/n(n2r)l[Ln−l−12l+1(n2r)]Ylm(θ,ϕ)
其中非常棒的是 l a g u e r r e laguerre laguerre 多项式 L n − l − 1 2 l + 1 ( 2 r n ) L_n-l-1^2 l+1\\left(\\frac2 rn\\right) Ln−l−12l+1(n2r)，MATLAB中有自带的函数 laguerreL可以使用，但是球谐函数(SphericalHarmonicY) Y l m ( θ , ϕ ) Y_l^m(\\theta, \\phi) Ylm(θ,ϕ)，并不是MATLAB的自带函数，不过好在，当 m ≥ 0 m\\ge0 m≥0时球谐函数的展开式：
Y
l
m
(
θ
,
ϕ
)
=
(
−
1
)
m
(
2
l
+
1
)
4
π
(
l
−
∣
m
∣
)
!
(
l
+
∣
m
∣
)
!
e
i
m
ϕ
P
l
m
(
cos
θ
)
Y_l^m(\\theta, \\phi)=(-1)^m \\sqrt\\frac(2 l+1)4 \\pi \\frac(l-|m|) !(l+|m|) ! e^i m \\phi P_l^m(\\cos \\theta)
Ylm(θ,ϕ)=(−1)m4π(2l+1)(l+∣m∣)!(l−∣m∣)!eimϕPlm(cosθ)
其中
L
e
g
e
n
d
r
e
Legendre
Legendre 函数
P
l
m
(
cos
θ
)
P_l^m(\\cos \\theta)
Plm(cosθ):
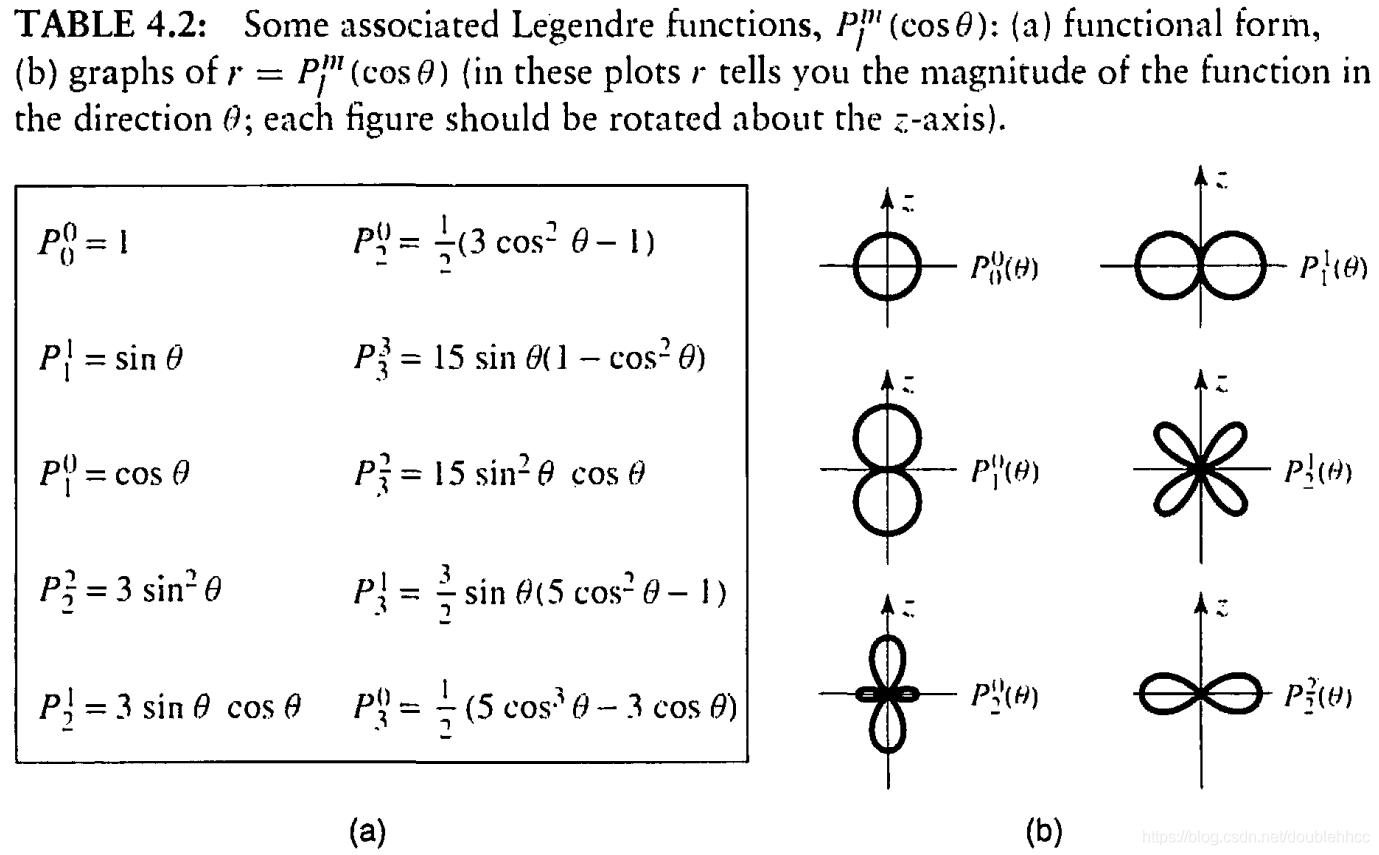
虽然，也很复杂。。但是耐不住MATLAB自带这个函数啊，甚至MATLAB还给出了如何通过该函数生成球谐函数的实例，简直太贴心了，爱了爱了：
dx=pi/60;
col=0:dx:pi;
az=0:dx:2*pi;
[phi,theta]=meshgrid(az,col);
% 计算 l=3 的网格上的 P_l^m(\\cos \\theta)
l=3;
Plm=legendre(l,cos(theta));
% 由于 legendre 为 m 的所有值计算答案，因此 Plm 会包含一些额外的函数值。
% 提取 m=2 的值并丢弃其余值。
% 使用 reshape 函数将结果定向为与 phi 和 theta 具有相同大小的矩阵。
m=2;
if l~=0
Plm=reshape(Plm(m+1,:,:),size(phi));
end
% 计算Y_3^2的球谐函数值
a=(2*l+1)*factorial(l-m);
b=4*pi*factorial(l+m);
C=sqrt(a/b);
Ylm=C.*Plm.*exp(1i*m*phi);
% 球面坐标转换为笛卡尔坐标并绘图
[Xm,Ym,Zm]=sph2cart(phi,pi/2-theta,abs(real(Ylm)));
surf(Xm,Ym,Zm)
title('$Y_3^2$ spherical harmonic','interpreter','latex')
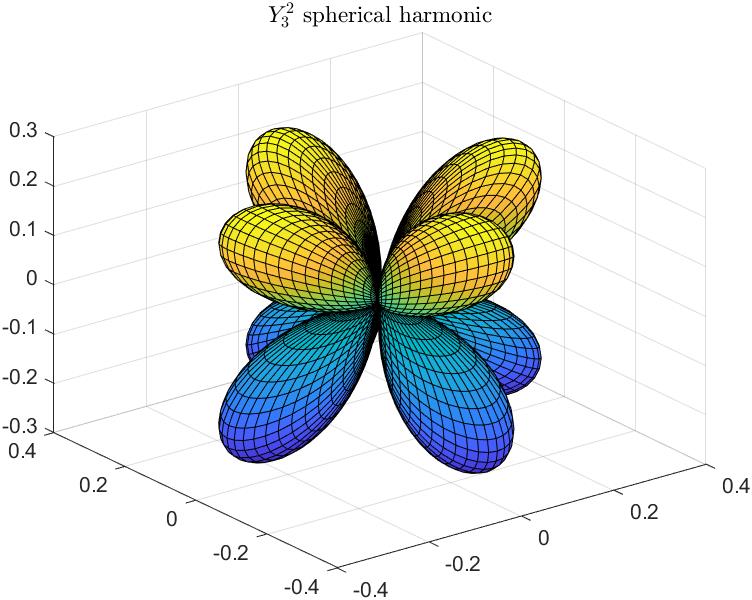
万事俱备开始编程：
工具函数
function psi=HydWave(n,l,m,x,y,z)
% @author:slandarer
% 由坐标点计算向量模长及角度
r=vecnorm([x(:),y(:),z(:)]')';
theta=atan2(vecnorm([x(:),y(:)]')',z(:));
phi=atan2(y(:),x(:));
% 恢复矩阵型状
r=reshape(r,size(x));
theta=reshape(theta,size(x));
phi=reshape(phi,size(x)一维谐振子定态 Schrödinger 方程的数值解法
图像分解基于matlab GUI二维图像小波分解含Matlab源码 2297期