红黑树操作
Posted Keep--Silent
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了红黑树操作相关的知识,希望对你有一定的参考价值。
前言
AVL的插入和删除操作,会频繁地调整全树的结构,代价较大。因此,在AVL的平衡标准上放宽条件,引入红黑树。
目录
性质
定义
①每个结点是红色或者黑色
②根结点是黑色。
③每个叶子结点都是黑色的空结点(NUUL结点)。
④不存在两个相邻的红节点。(即红节点之父和红节点之子必是黑)
⑤从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
推论
①从根节点到叶节点的最长路径不超过最短路径的两倍
②有n个内部结点的红黑树的高度 h ≤ 2 log 2 ( n + 1 ) h\\leq 2\\log_2(n+1) h≤2log2(n+1)
插入
新插入结点定义为红色,分五种情况进行操作。
先约定一下命名规则
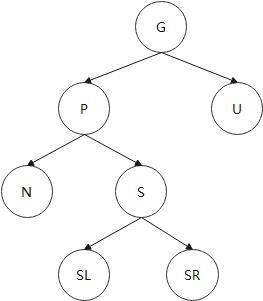
G G G是祖父结点 G r a n d f a t h e r Grandfather Grandfather
P P P是父节点 P a r e n t Parent Parent, U U U是叔结点 U n c l e Uncle Uncle
N N N是当前结点 N o w N o d e , S Now Node,S NowNode,S是兄弟结点 S i b l i n g Sibling Sibling
S L SL SL是兄弟结点的左节点 L e f t , S R Left,SR Left,SR是兄弟结点的右节点 R i g h t Right Right
情况一
N为根:
N直接染黑
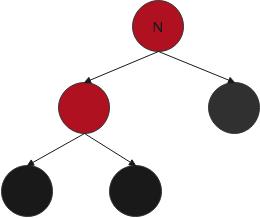
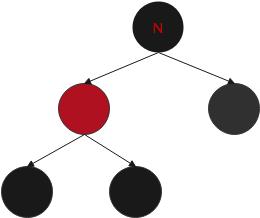
情况二
P为黑
不变
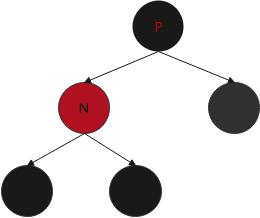
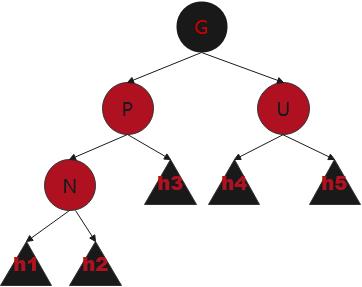
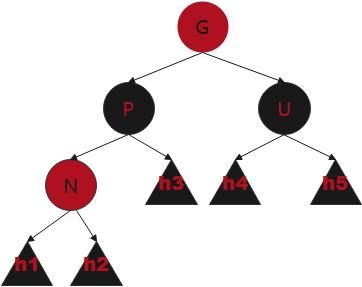
情况三
P为红(所以G为黑),U为红:
P染黑,U染黑,G染红,然后递归向上调整。
情况四
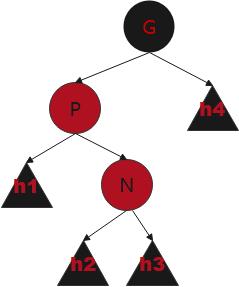
P为红(所以G为黑),U为黑,N的大小介于P和G
P旋转到N的下面(即N父为G,N子为P),转为情况五
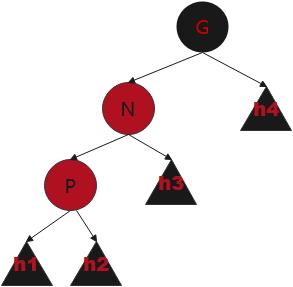
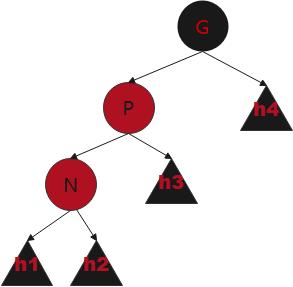
情况五
P为红(所以G为黑),U为黑,P的大小介于N和G(即一头偏)
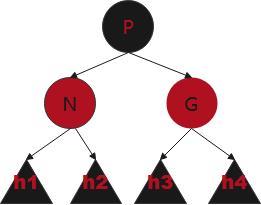
P旋转到G的上方(即P子为NG),P染黑,G染红
以上是关于红黑树操作的主要内容,如果未能解决你的问题,请参考以下文章