20180616小测
Posted cmd2001
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了20180616小测相关的知识,希望对你有一定的参考价值。
论连续8天考试5场是怎样的体验......
我已经,不想再考试了啊......
(所以这就是你全程弃疗的理由?)
T1:

显然这题面里给的最后那个示例是错的......
观察到75分长度不超过1e5,我们可以大力数位DP:
f[i][j][k][p]表示长为i,首位k,最大2L-Z前缀数值为k,最小2L-Z前缀数值为P的方案数。
转移的话,枚举填哪个字符看是否合法即可转移;统计答案枚举前多少位相同即可。
这样就get到了75分,当时感觉正解大概是矩阵化什么的,然后弃疗了。
正解的确是矩阵化,但不是这样做的。
(显然这种两边拼凑形式的DP没法变成矩阵啊)
我们令f[i][j][k][p]表示前i位,是否与给定串完全相同,最大2L-Z后缀数值为k,最小2L-Z后缀数值为P的方案数。
显然这个转移可以矩阵化,然后在展开字符串的时候快速幂一发就能AC啦。
(为什么这种省选难度题我都不会了啊)
考场75分代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cassert> 6 #define debug cout 7 typedef long long int lli; 8 using namespace std; 9 const int maxn=1e5+1e2,lim=1e5; 10 const int mod=998244353; 11 12 char s[maxn]; 13 int in[maxn]; 14 int n,ans; 15 16 inline int& f(int i,int j,int k,int p) { 17 static int arr[maxn][2][4][4]; 18 return arr[i][j][k+3][p+3]; 19 } 20 inline void adde(int &dst,const int &x) { 21 if( ( dst += x ) >= mod ) dst -= mod; 22 } 23 24 inline void dp() { // 0 means l , 1 means z . 25 f(0,0,0,0) = 1; 26 for(int i=0;i<lim;i++) for(int j=0;j<2;j++) for(int k=0;k<=3;k++) for(int p=-3;p<=0;p++) if(f(i,j,k,p)) { 27 if( k + 2 <= 3 ) adde(f(i+1,0,max(k+2,2),min(p+2,0)),f(i,j,k,p)); 28 if( p - 1 >= -3 ) adde(f(i+1,1,max(k-1,0),min(p-1,-1)),f(i,j,k,p)); 29 } 30 } 31 32 inline void getans() { 33 int mx = 0 , mi = 0; ans = 1; 34 for(int i=1,rit;i<=n;i++) { // diff at bit[i] . 35 rit = n - i + 1; 36 for(int j=0;j<in[i];j++) for(int k=0;k<=3;k++) for(int p=-3;p<=0;p++) if( mx + k <= 3 && mi + p >= -3 ) adde(ans,f(rit,j,k,p)); 37 if( !in[i] ) mx = max(mx+2,2) , mi = min(mi+2,0); 38 else mx = max(mx-1,0) , mi = min(mi-1,-1); 39 } 40 } 41 42 43 inline int findint(const string &x) { 44 int ret = 0; 45 for(unsigned i=0;i<x.length();i++) { 46 if( isdigit(x[i]) ) ret = ret * 10 + x[i] - ‘0‘; 47 else break; 48 } 49 return ret; 50 } 51 inline string cutint(const string &x) { 52 int i; 53 for(i=0;i<(signed)x.length();i++) if( !isdigit(x[i]) ) break; 54 return x.substr(i,x.length()-i); 55 } 56 inline string explain(const string &x) { 57 int i,j; 58 for(i=0;i<(signed)x.length();i++) if( x[i] == ‘(‘ ) break; 59 if( i == (signed)x.length() ) return x; 60 int su = 0; 61 for(j=0;j<(signed)x.length();j++) { 62 if( x[j] == ‘(‘ ) ++su; 63 else if( x[j] == ‘)‘ ) { 64 if( su > 1 ) --su; 65 else break; 66 } 67 } 68 string ret = x.substr(0,i) , mid = x.substr(i+1,j-i-1) , rem = x.substr(j+1,x.length()-j-1) , rit = cutint(rem); 69 int tim = findint(rem); 70 mid = explain(mid); 71 while(tim--) ret = ret + mid; 72 ret = ret + explain(rit); 73 return ret; 74 } 75 inline void explain() { 76 string ss = s; 77 string ex = explain(ss); 78 n = ex.length(); 79 for(int i=1;i<=n;i++) in[i] = ex[i-1] == ‘Z‘; 80 } 81 82 int main() { 83 static int T; 84 scanf("%d",&T) , dp(); 85 while(T-- ) { 86 scanf("%s",s) , explain() , getans(); 87 printf("%d ",ans); 88 } 89 return 0; 90 }
正解代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define debug cout 6 typedef long long int lli; 7 using namespace std; 8 const int maxn=5e2+1e1,maxs=33,lim=32; 9 const int mod=998244353; 10 11 char in[maxn]; 12 13 inline int add(const int &x,const int &y) { 14 const int ret = x + y; 15 return ret >= mod ? ret - mod : ret; 16 } 17 inline int mul(const int &x,const int &y) { 18 return (lli) x * y % mod; 19 } 20 inline void adde(int &dst,const int &x) { 21 if( ( dst += x ) >= mod ) dst -= mod; 22 } 23 24 struct Matrix { 25 int dat[maxs][maxs]; 26 Matrix(int tpe=0) { memset(dat,0,sizeof(dat)); for(int i=1;i<=lim;i++) dat[i][i] = tpe; } 27 int* operator [] (const int &x) { return dat[x]; } 28 const int * operator [] (const int &x) const { return dat[x]; } 29 friend Matrix operator + (const Matrix &a,const Matrix &b) { 30 Matrix ret; 31 for(int i=1;i<=lim;i++) for(int j=1;j<=lim;j++) ret[i][j] = add(a[i][j],b[i][j]); 32 return ret; 33 } 34 friend Matrix operator * (const Matrix &a,const Matrix &b) { 35 Matrix ret; 36 for(int i=1;i<=lim;i++) for(int j=1;j<=lim;j++) for(int k=1;k<=lim;k++) adde(ret[i][j],mul(a[i][k],b[k][j])); 37 return ret; 38 } 39 inline void print() const { 40 for(int i=1;i<=32;i++) { 41 for(int j=1;j<=32;j++) debug<<dat[i][j]<<" "; 42 debug<<endl; 43 } 44 } 45 }trans[2],ini; 46 47 inline int cov(int issame,int mx,int mi) { // c in range[0,1] , mx in range[-3,0] , mi in range[0,3] . 48 return issame * 16 + mx * 4 + mi + 4; 49 } 50 inline void buildtrs() { 51 for(int j=0;j<2;j++) for(int k=0;k<=3;k++) for(int p=-3;p<=0;p++) { 52 if( k + 2 <= 3 ) { 53 trans[0][cov(1,k,p)][cov(1,max(k+2,2),min(p+2,0))] = 1; 54 trans[0][cov(0,k,p)][cov(0,max(k+2,2),min(p+2,0))] = 1; 55 trans[1][cov(1,k,p)][cov(0,max(k+2,2),min(p+2,0))] = 1; 56 trans[1][cov(0,k,p)][cov(0,max(k+2,2),min(p+2,0))] = 1; 57 } 58 if( p - 1 >= -3 ) { 59 trans[0][cov(0,k,p)][cov(0,max(k-1,0),min(p-1,-1))] = 1; 60 trans[1][cov(1,k,p)][cov(1,max(k-1,0),min(p-1,-1))] = 1; 61 trans[1][cov(0,k,p)][cov(0,max(k-1,0),min(p-1,-1))] = 1; 62 } 63 } 64 ini[1][cov(1,0,0)] = 1; 65 } 66 67 inline Matrix fastpow(Matrix base,int tim) { 68 Matrix ret(1); 69 while(tim) { 70 if( tim & 1 ) ret = ret * base; 71 if( tim >>= 1 ) base = base * base; 72 } 73 return ret; 74 } 75 inline Matrix getseg(const string &x) { 76 Matrix ret(1); 77 for(int i=0;i<(signed)x.size();i++) ret = ret * trans[x[i]==‘Z‘]; 78 return ret; 79 } 80 inline int findint(const string &x) { 81 int ret = 0; 82 for(unsigned i=0;i<x.length();i++) { 83 if( isdigit(x[i]) ) ret = ret * 10 + x[i] - ‘0‘; 84 else break; 85 } 86 return ret; 87 } 88 89 inline string cutint(const string &x) { 90 int i; 91 for(i=0;i<(signed)x.length();i++) if( !isdigit(x[i]) ) break; 92 return x.substr(i,x.length()-i); 93 } 94 inline Matrix explain(const string &x) { 95 int i,j; 96 for(i=0;i<(signed)x.length();i++) if( x[i] == ‘(‘ ) break; 97 if( i == (signed)x.length() ) return getseg(x); 98 int su = 0; 99 for(j=0;j<(signed)x.length();j++) { 100 if( x[j] == ‘(‘ ) ++su; 101 else if( x[j] == ‘)‘ ) { 102 if( su > 1 ) --su; 103 else break; 104 } 105 } 106 string lft = x.substr(0,i) , mid = x.substr(i+1,j-i-1) , rem = x.substr(j+1,x.length()-j-1) , rit = cutint(rem); 107 Matrix ret = getseg(lft) * fastpow(explain(mid),findint(rem)) * explain(rit); 108 return ret; 109 } 110 inline int solve(const string &x) { 111 Matrix ans = ini * explain(x); 112 int ret = 0; 113 for(int i=1;i<=lim;i++) adde(ret,ans[1][i]); 114 return ret; 115 } 116 117 int main() { 118 static int T; 119 scanf("%d",&T) , buildtrs(); 120 while(T--) scanf("%s",in+1) , printf("%d ",solve((string)(in+1))); 121 return 0; 122 }
T2:

看到这么多SubTask......
首先答案就是排好序后的偶数项和减奇数项和。另外答案可以直接用unsigned long long存,运算过程中即使爆掉了也没有关系,反正最终答案在范围内即可。
SubTask12,直接枚举起始点用非旋转treap维护排好序的序列即可;SubTask3,可以统计每个数字在奇数位或者偶数位的共线,手玩一下就好了;SubTask4,只有存在奇数个1的区间对答案贡献1,手玩一下也就好了。
好的,你get到了60分,想不到正解,可以弃疗了。
正解的确是统计贡献,但是不是统计单点贡献,而是统计区间贡献。
考虑我们把点值排好序后的每个区间,会被计入答案多少次。我们将<=这个区间左端点的数值变成0,>=这个区间右端点的数值变成1,那么,这个区间被计入答案的可选原序列区间一定包含奇数个1。
然后线段树维护一下就行了,区间取反,统计01,线段树的基本操作。
(为什么这种NOIP数据结构题我也不会了啊)
考场60分代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cassert> 6 #define debug cout 7 typedef unsigned long long int ulli; 8 using namespace std; 9 const int maxn=3e5+1e2; 10 11 int in[maxn],n; 12 ulli ans; // ans will be correct moding 2 ^ 64 . 13 14 namespace Force { 15 const int maxn=2e3+1e2; 16 struct pii {int l,r;}; 17 struct RotatelessTreap { 18 int ch[maxn][2],siz[maxn],fix[maxn]; 19 ulli dat[maxn],su[maxn][2]; // 0 means even , 1 means odd . 20 RotatelessTreap() { 21 for(int i=0;i<maxn;i++) fix[i] = i; 22 random_shuffle(fix,fix+maxn); 23 } 24 inline void maintain(int pos) { 25 siz[pos] = siz[ch[pos][0]] + siz[ch[pos][1]] + 1; 26 if( ! ( siz[ch[pos][0]] & 1 ) ) { 27 su[pos][0] = su[ch[pos][0]][0] + su[ch[pos][1]][1]; 28 su[pos][1] = su[ch[pos][0]][1] + dat[pos] + su[ch[pos][1]][0]; 29 } else { 30 su[pos][0] = su[ch[pos][0]][0] + dat[pos] + su[ch[pos][1]][0]; 31 su[pos][1] = su[ch[pos][0]][1] + su[ch[pos][1]][1]; 32 } 33 } 34 inline pii split(int pos,ulli nv) { // left is <= nv . 35 if( !pos ) return (pii){0,0}; 36 if( dat[pos] > nv ) { 37 pii spl = split(ch[pos][0],nv); 38 ch[pos][0] = spl.r , maintain(pos); 39 return (pii){spl.l,pos}; 40 } else { 41 pii spr = split(ch[pos][1],nv); 42 ch[pos][1] = spr.l , maintain(pos); 43 return (pii){pos,spr.r}; 44 } 45 } 46 inline int merge(int x,int y) { // assert dat[x] <= dat[y] . 47 if( !x || !y ) return x | y; 48 assert(dat[x]<=dat[y]); 49 if( fix[x] > fix[y] ) { 50 ch[x][1] = merge(ch[x][1],y) , maintain(x); 51 return x; 52 } else { 53 ch[y][0] = merge(x,ch[y][0]) , maintain(y); 54 return y; 55 } 56 } 57 inline void reset(int x,ulli dd) { 58 su[x][0] = ch[x][0] = ch[x][1] = 0 , su[x][1] = dat[x] = dd , siz[x] = 1; 59 } 60 inline void insert(int &root,int x) { 61 pii sp = split(root,dat[x]); 62 root = merge(sp.l,merge(x,sp.r)); 63 } 64 inline ulli query(int root) { 65 return su[root][0] - su[root][1]; 66 } 67 }treap; 68 69 inline void getans() { 70 for(int i=1,root;i<=n;i++) { 71 treap.reset(root=i,in[i]); 72 for(int j=i+1;j<=n;j++) { 73 treap.reset(j,in[j]) , treap.insert(root,j); 74 if( ( j - i ) & 1 ) ans += treap.query(root); 75 } 76 } 77 } 78 } 79 80 namespace Order { 81 inline ulli calc_odd(int i) { 82 int before = i , after = n - i; 83 return (ulli) ( ( before + 1 ) >> 1 ) * (ulli) ( ( after + 1 ) >> 1 ); 84 } 85 inline ulli calc_even(int i) { 86 int before = i , after = n - i; 87 return (ulli) ( before >> 1 ) * (ulli) ( ( after >> 1 ) + 1 ); 88 } 89 inline void getans() { 90 for(int i=1;i<=n;i++) ans += calc_even(i) * in[i] , ans -= calc_odd(i) * in[i]; 91 } 92 } 93 94 namespace Less { 95 int su[maxn],prf[2][2]; 96 inline void getans() { 97 for(int i=1;i<=n;i++) su[i] = su[i-1] + in[i]; 98 prf[0][0] = 1; 99 for(int i=1;i<=n;i++) ans += prf[i&1][(su[i]&1)^1] , ++prf[i&1][su[i]&1]; 100 } 101 } 102 103 int main() { 104 static bool order = 1 , less = 1; 105 scanf("%d",&n); 106 for(int i=1;i<=n;i++) { 107 scanf("%d",in+i); 108 if( i != 1 && in[i] < in[i-1] ) order = 0; 109 if( in[i] > 1 ) less = 0; 110 } 111 if( n <= 2000 ) Force::getans(); 112 else if( order ) Order::getans(); 113 else if( less ) Less::getans(); 114 else srand((unsigned long long)new char) , ans = rand() * rand(); 115 printf("%llu ",ans); 116 return 0; 117 }
正解代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #define debug cout 7 typedef unsigned long long int ulli; 8 using namespace std; 9 const int maxn=3e5+1e2; 10 11 struct SegmentTree { 12 ulli su[maxn<<2][2]; 13 bool lazy[maxn<<2]; 14 #define lson(pos) (pos<<1) 15 #define rson(pos) (pos<<1|1) 16 inline void maintain(int pos) { 17 for(int i=0;i<2;i++) su[pos][i] = su[lson(pos)][i] + su[rson(pos)][i]; 18 } 19 inline void apply(int pos) { 20 swap(su[pos][0],su[pos][1]) , lazy[pos] ^= 1; 21 } 22 inline void push(int pos) { 23 if( lazy[pos] ) apply(lson(pos)) , apply(rson(pos)) , lazy[pos] ^= 1; 24 } 25 inline void build(int pos,int l,int r,const int &fix) { // fix will be 1 if build even . 26 if( l == r ) return void( su[pos][0] = ( l & 1 ) ^ fix ); 27 const int mid = ( l + r ) >> 1; 28 build(lson(pos),l,mid,fix) , build(rson(pos),mid+1,r,fix) , maintain(pos); 29 } 30 inline void update(int pos,int l,int r,const int &ll,const int &rr) { 31 if( ll <= l && r <= rr ) return apply(pos); 32 const int mid = ( l + r ) >> 1; push(pos); 33 if( ll <= mid ) update(lson(pos),l,mid,ll,rr); 34 if( mid < rr ) update(rson(pos),mid+1,r,ll,rr); 35 maintain(pos); 36 } 37 inline ulli query() { 38 return su[1][0] * su[1][1]; 39 } 40 }sgt[2]; 41 42 int in[maxn],srt[maxn],len,n; 43 vector<int> app[maxn]; 44 ulli ans; 45 46 int main() { 47 scanf("%d",&n); 48 for(int i=1;i<=n;i++) scanf("%d",in+i) , srt[i] = in[i]; 49 std::sort(srt+1,srt+1+n) , len = unique(srt+1,srt+1+n) - srt - 1; 50 for(int i=1;i<=n;i++) app[in[i]=lower_bound(srt+1,srt+1+len,in[i])-srt].push_back(i); 51 for(int i=0;i<2;i++) sgt[i].build(1,0,n,i^1); 52 for(int i=len;i>1;i--) { 53 for(unsigned j=0;j<app[i].size();j++) for(int k=0;k<2;k++) sgt[k].update(1,0,n,app[i][j],n); 54 for(int j=0;j<2;j++) ans += ( srt[i] - srt[i-1] ) * sgt[j].query(); 55 } 56 printf("%llu ",ans); 57 return 0; 58 }
T3:

看到这题第一想法:谁先取模再gcd谁sb。
感觉是杜教筛筛phi之类的东西,然而并推不出可行的计算式......然后就弃疗爆零啦!
正解是这样的: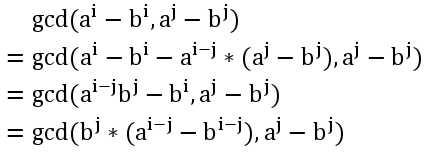
又因为: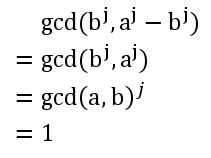
所以我们的上标就能辗转相除啦: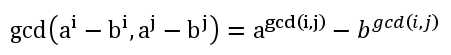
然后我们分离AB单独计算: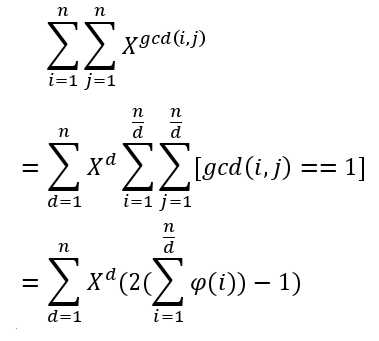
(左边的X^d可以等比数列求和,右边gcd的那个变换,不懂的话,可以退役了)
于是杜教筛一发phi就好了。
(为什么这种莫比乌斯反演板子题都不会了啊,我这数论怕是都白学了)
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<unordered_map> 6 #define debug cout 7 typedef long long int lli; 8 using namespace std; 9 const int maxn=5e7+1e2,lim=5e7; 10 const int mod=998244353; 11 12 namespace Sieve { 13 lli phi[maxn]; 14 inline void sieve() { 15 static int prime[maxn/10],cnt; 16 static bool vis[maxn]; 17 phi[1] = 1; 18 for(int i=2;i<=lim;i++) { 19 if( !vis[i] ) prime[++cnt] = i , phi[i] = i - 1; 20 for(int j=1;j<=cnt&&(lli)i*prime[j]<=lim;j++) { 21 const int t = i * prime[j]; 22 vis[t] = 1; 23 if( i % prime[j] ) phi[t] = phi[i] * ( prime[j] - 1 ); 24 else { phi[t] = phi[i] * prime[j]; break; } 25 } 26 } 27 for(int i=1;i<=lim;i++) phi[i] = ( phi[i] + phi[i-1] ) % mod; 28 } 29 unordered_map<lli,lli> mp; 30 inline lli calc(lli x) { 31 if( x <= lim ) return phi[x]; 32 if( mp.find(x) != mp.end() ) return mp[x]; 33 lli ret = ( ( x % mod ) * ( x % mod + 1 ) >> 1 ) % mod; 34 for(lli i=2,j;i<=x;i=j+1) { 35 j = x / ( x / i ); 36 ret -= ( j - i + 1 ) % mod * calc( x / i ) % mod , ret %= mod; 37 } 38 return mp[x] = ( ret + mod ) % mod; 39 } 40 } 41 42 inline lli fastpow(lli base,lli tim) { 43 lli ret = 1; 44 while(tim) { 45 if( tim & 1 ) ret = ret * base % mod; 46 if( tim >>= 1 ) base = base * base % mod; 47 } 48 return ret; 49 } 50 inline lli supow(lli x,lli inv,lli n) { 51 if( x == 1 ) return n; 52 lli t = ( fastpow(x,n+1) - 1 + mod ) % mod; 53 return t * inv % mod; 54 } 55 inline lli calc(lli x,lli n) { 56 const lli inv = fastpow(x-1,mod-2); 57 lli ret = 0; 58 for(lli i=1,j;i<=n;i=j+1) { 59 j = n / ( n / i ); 60 ret += ( supow(x,inv,j) - supow(x,inv,i-1) + mod ) % mod * ( ( 2 * Sieve::calc(n/i) % mod - 1 + mod ) % mod ) % mod , ret %= mod; 61 } 62 return ret; 63 } 64 65 66 int main() { 67 static int T; 68 static lli n,a,b; 69 scanf("%d",&T) , Sieve::sieve(); 70 while(T--) scanf("%lld%lld%lld",&n,&a,&b) , printf("%lld ",(calc(a,n)-calc(b,n)+mod)%mod); 71 return 0; 72 }
そう 理想 望むだけ きっと
那样的 理想 只是希望着的话 一定
もう 死のう 思うだけ きっと
只是 死掉算了 这样想着的话 一定
明日になれば ほら
如果到了明天的话 你看
きっと もう 忘れて
一定 已经 忘掉了
以上是关于20180616小测的主要内容,如果未能解决你的问题,请参考以下文章
