基于集成算法投票的波士顿房价数据集回归问题

Posted 2022-03-30 ZHW_AI课题组

基于集成算法投票的波士顿房价数据集回归问题

• 1. 作者介绍
• 2．关于理论方面的知识介绍
• • • 2.1 集成学习
    • 2.2 随机森林
    • 2.3 数据集介绍
• 3．实验相关
• • • 3.1实验代码
    • 3.2实现效果
    • • 3.2.1 拟合曲线
      • 3.2.2 拟合优度
    • 3.3问题与分析
    • • 3.3.1基学习器学习权重和错误率的关系
      • 3.3.2拟合曲线
• 4．参考

1. 作者介绍

成帅凯，男，西安工程大学电子信息学院，21级研究生
研究方向：机器视觉与人工智能
电子邮件：[e-mail]

孟莉苹，女，西安工程大学电子信息学院，2021级硕士研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：[e-mail]

2．关于理论方面的知识介绍

2.1 集成学习

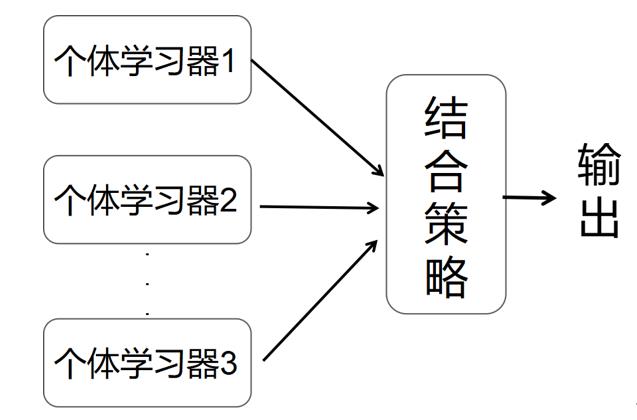
集成学习(ensemble learning)是通过构建并结合多个学习器来完成学习任务。集成学习可以用于分类问题集成、回归问题集成、特征选取集成、异常点检测集成等。投票机制(voting)是集成学习里面针对分类回归问题的一种结合策略，基本思想是融合多个数据来降低误差。对于回归模型最终的预测结果是多个其他回归预测结果的平均值。
根据个体学习器的生成方式，目前的集成学习方法大致分为两大类。即个体学习器间存在强依赖关系，必须串行生成的序列化方法，以及个体学习器间不存在强依赖关系，可同时生成的并行化方法:前者的代表是提升法(Boosting),后者的代表是装袋法(bagging)。

2.2 随机森林

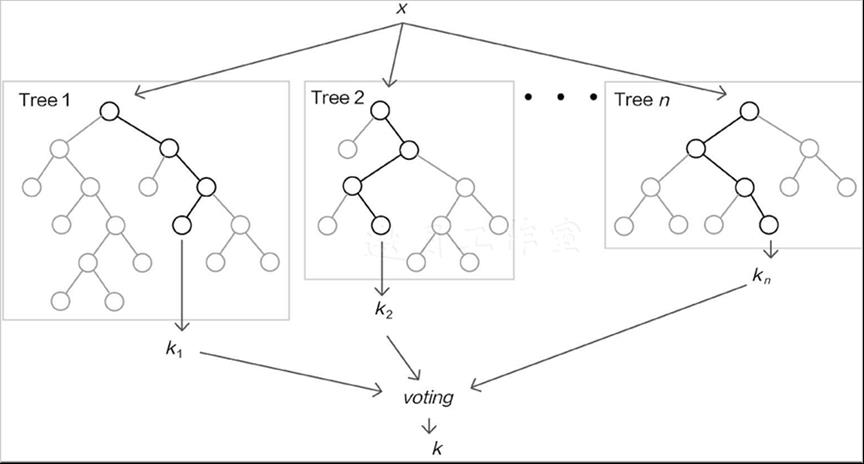
随机森林(Random Forest,简称RF)是Bagging的一个扩展变体。RF在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。具体来说，传统决策树在选择划分属性时在当前节点的属性集合中选择一个最优属性；而在RF中，对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最优属性用于划分。

2.3 数据集介绍

波士顿房价数据集统计的是20世纪70年代中期波士顿郊区房价的中位数，统计了城镇人均犯罪率、不动产税等共计13个指标，506条房价数据，通过统计出的房价，试图能找到那些指标与房价的关系。
数据集中的每一行数据都是对波士顿周边或城镇房价的情况描述，下面对数据集变量进行说明，方便大家理解数据集变量代表的意义。
CRIM: 城镇人均犯罪率
ZN: 住宅用地所占比例
INDUS: 城镇中非住宅用地所占比例
CHAS: 虚拟变量,用于回归分析
NOX: 环保指数
RM: 每栋住宅的房间数
AGE: 1940 年以前建成的自住单位的比例
DIS: 距离 5 个波士顿的就业中心的加权距离
RAD: 距离高速公路的便利指数
TAX: 每一万美元的不动产税率
PTRATIO: 城镇中的教师学生比例
B: 城镇中的黑人比例
LSTAT: 地区中有多少房东属于低收入人群
MEDV: 自住房屋房价中位数（也就是均价）

3．实验相关

3.1实验代码

import numpy as np
from matplotlib.ticker import MultipleLocator
from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.ensemble import AdaBoostRegressor,  RandomForestRegressor
boston = load_boston()
features = boston.data # 特征集
prices = boston.target # 目标集
X_train, X_test, y_train, y_test = train_test_split(features, prices,test_size=0.4)

def suanfa():
    train_x, test_x, train_y, test_y = train_test_split(features, prices, test_size=0.25, random_state=33)
    regressor = AdaBoostRegressor()  # 均采用默认参数
    regressor.fit(train_x, train_y)  # 拟合模型
    pred_y = regressor.predict(test_x)
    mse = mean_squared_error(test_y, pred_y)
    print('score:'.format(r2_score(test_y, pred_y)))
    print("AdaBoost 均方误差 = ", round(mse, 2)) # 18.57
    print(len(regressor.estimators_))
    print(regressor.estimator_weights_)
    print(regressor.estimator_errors_)
    plt.plot(regressor.estimator_errors_, label='error', color='orange')
    plt.plot(regressor.estimator_weights_, label='weights', color='blue')
    plt.legend(loc='best')  # 显示图例
    n = np.arange(0, test_x.shape[0], 1)
    plt.figure(figsize=(8, 5))  # 设置图片格式
    plt.plot(n,  pred_y, c='r', label='prediction', lw=2)  # 画出拟合曲线
    plt.plot(n, test_y, c='b', label='true', lw=2)  # 画出拟合曲线
    plt.axis('tight')  # 使x轴与y轴限制在有数据的区域
    plt.title("AdaBoostRegressor")
    plt.show()


def suanfa1():
   X_train, X_test, y_train, y_test = train_test_split(features, prices,test_size=0.4)
   regressor = RandomForestRegressor(n_estimators=100, max_depth=3, random_state=0)
   regressor.fit(X_train, y_train)  # 拟合模型
   result = regressor.predict(X_test)
   print('score:'.format(r2_score(y_test, result)))  # 显示训练结果与测试结果的拟合优度
   n = np.arange(0, X_test.shape[0], 1)
   plt.figure(figsize=(8, 5))  # 设置图片格式
   plt.plot(n, result, c='r', label='prediction', lw=2)  # 画出拟合曲线
   plt.plot(n, y_test, c='b', label='tru

3.2实现效果

3.2.1 拟合曲线

3.2.2 拟合优度

调用随机森林算法的拟合优度

调用多层神经网络的拟合优度

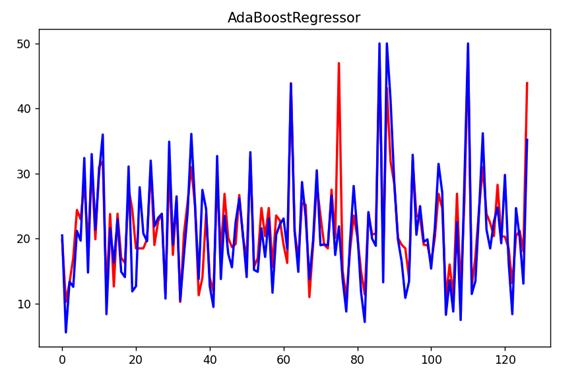
调用AdaBoost方法预测值和真实值之间的相关性

3.3问题与分析

由于借鉴之前同学的经验，本次问题解决程序方面问题极少，主要问题存在于对题目的审查，最开始利用AdaBoost算法实现了功能，但是不符合投票的结合策略。但该方法准确率和实时性结合来看相对优秀，因此在这里简单介绍，程序如上suanfa函数。
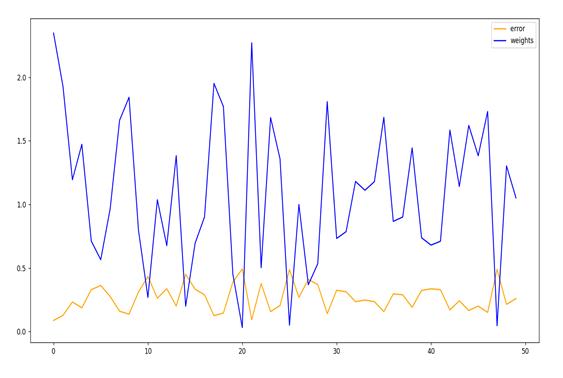
AdaBoost是经典的Boosting算法，该算法要求基学习器能对特定的数据分布进行学习，这可以通过“重赋权法”(re-weighting)实施，即在训练过程的每一轮中，根据样本分布为每个训练样本重新赋予一个权重。对无法接受带权样本的基学习算法，则可以通过“重采样法”(re-sampling)来处理，即在每一轮学习中，根据样本分布对训练集重新进行采样，再用重采样获得的样本集对基学习器进行训练。显然可得，在结合策略上是经典的平均法。

3.3.1基学习器学习权重和错误率的关系

3.3.2拟合曲线

4．参考

周志华.机器学习[M].北京:清华大学出版社,2016:425.