LFO 低频振荡器简介及其 C/C++ 实现

Posted 2022-03-29 芥末的无奈

文章目录

• 前言
• LFO 算法
• • LFO 基本实现
  • 向其他波形变换
• 总结
• 参考

---

前言

LFO 即 “Low Frequency Oscillator” 低频振荡器，它可以按照各类波形（例如锯齿波、三角波、Sine 波等）进行震动。

名副其实，LFO 的振荡频率通常都低于 20HZ，低于人类听觉范围。那么，为什么我们想要一个听不到的振荡器？在音效处理中，我们使用 LFO 来控制音效算法中的某些参数，为听到的声音赋予生命和动感，例如 Vibrator、Flanger 和 Chorus 等。

LFO 算法

LFO 基本实现

LFO 的设计和实现都很简单，它通常有两个重要的变量：

• modulo 计数器，它从 0 开始计数到 1.0，一旦到达或者超过 1.0，它会反转为 0。
• inc 增量，modulo 计算器每次都会加上 inc 来增加。inc 增量的值与振荡器频率相关，具体的计算我们后面会细说。

伪代码如下：

for(int i = 0; i < N; ++i)

	modulo += inc;
	if(modulo > 1.0f)
		modulo = 0.0f;

那么 inc 应该如何计算呢？这与采样率和 LFO 频率有关。举个例子，例如 LFO 频率为 5 时，表示 1秒钟内，LFO 将会振荡来回 5 次。当采样率为 44100 时，意味着 1s 一共有 44100 个采样点，44100 个采样点里一共包含 5 个周期，因此每个周期包含 44100 / 5 = 8820 个点，而这 8820 个点表示的范围是 [0, 1]，因此每个点的增量 inc = 1/8820 = 5/44100：

float lfo_hz = 5;
float sample_rate = 44100;
inc = lfo_hz / sample_rate

向其他波形变换

上面提到实现中，我们得到了范围 [0, 1] 的波形。由于音频数据采样点数值范围都在 [-1, 1] 内，因此需要进行变换，让其值范围变换到 [-1,1]。这个过程也叫 单极转双极。

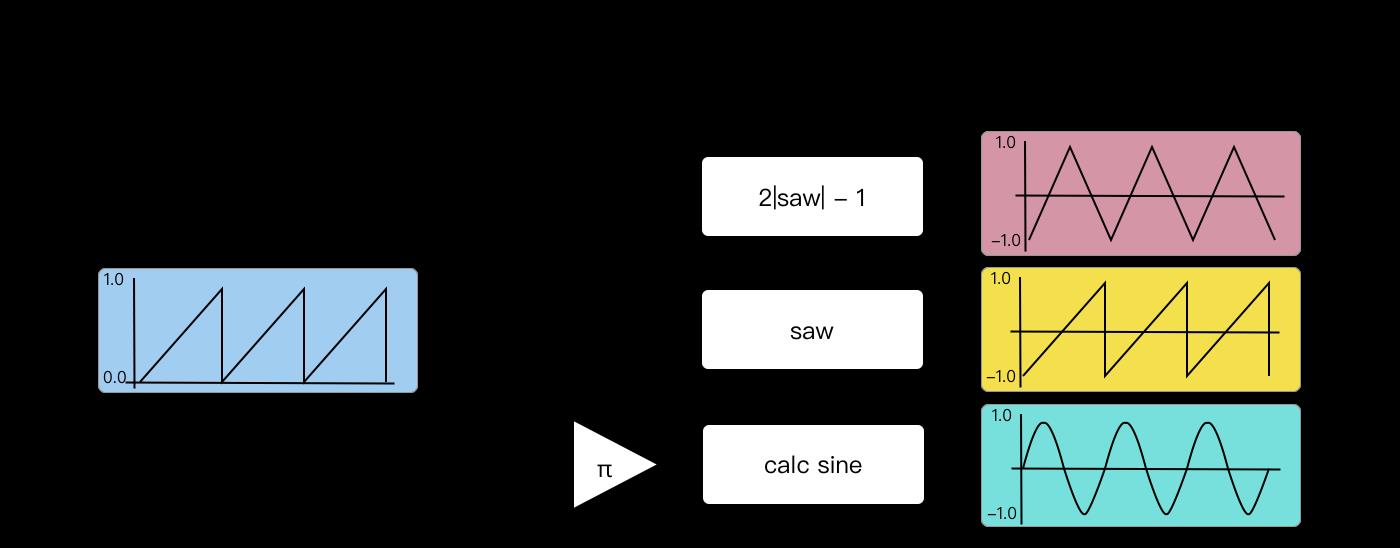
那么 [0, 1] 如何变换到 [-1, 1] 的锯齿波呢？十分简单：

saw = 2*module + 1;

那么三角波呢？基于锯齿波，我们可以这么做：

tra = 2*fabs(saw) - 1;

sine 波呢？我们这么做：

angle = 2 * M_PI * module;
sine = std::sin(angle);

然而，C/C++ 的 sin 是一个相当复杂的函数，LFO 或许不需要这么精确的值，因此我们希望用一种近似的方法来实现 sine 波，这种实现方式你可以在网络上找到：

double parabolicSine(double angle) 
    constexpr double B = 4.0 / M_PI;
    constexpr double C = -4.0 / (M_PI * M_PI);
    constexpr double P = 0.225;

    double y = B * angle + C * angle * fabs(angle);
    y = P * (y * fabs(y) - y) + y;
    return y;


angle = 2 * M_PI * module;
sine = parabolicSine(angle);

---

总结

介绍了 LFO 的作用以及 C/C++ 实现，完整的实现可以参考 Libaa - LFO。

---

参考

• What is a LFO and how to use it
• Libaa - LFO