分类问题与信息论基础（上）（DL笔记整理系列）

Posted 2022-03-24 繁凡さん

好吧，只好拆分为上下两篇发布了>_<

终于肝出来了，今天就是除夕夜了，祝大家新快乐！^q^

---

《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础 （上）（逻辑回归、Softmax回归、信息论基础）（DL笔记整理系列）

[e-mail]

https://fanfansann.blog.csdn.net/

https://github.com/fanfansann/fanfan-deep-learning-note

作者：繁凡

version 1.0  2022-1-20

 

声明：

1）《繁凡的深度学习笔记》是我自学完成深度学习相关的教材、课程、论文、项目实战等内容之后，自我总结整理创作的学习笔记。写文章就图一乐，大家能看得开心，能学到些许知识，对我而言就已经足够了 ^q^ 。

2）因个人时间、能力和水平有限，本文并非由我个人完全原创，文章部分内容整理自互联网上的各种资源，引用内容标注在每章末的参考资料之中。

3）本文仅供学术交流，非商用。所以每一部分具体的参考资料并没有详细对应。如果某部分不小心侵犯了大家的利益，还望海涵，并联系博主删除，非常感谢各位为知识传播做出的贡献！

4）本人才疏学浅，整理总结的时候难免出错，还望各位前辈不吝指正，谢谢。

5）本文由我个人（ CSDN 博主 「繁凡さん」（博客） ， 知乎答主 「繁凡」（专栏）， Github 「fanfansann」（全部源码） ， 微信公众号 「繁凡的小岛来信」（文章 P D F 下载））整理创作而成，且仅发布于这四个平台，仅做交流学习使用，无任何商业用途。

6）「我希望能够创作出一本清晰易懂、可爱有趣、内容详实的深度学习笔记，而不仅仅只是知识的简单堆砌。」

7）本文《繁凡的深度学习笔记》全汇总链接：《繁凡的深度学习笔记》前言、目录大纲

8）本文的Github 地址：https://github.com/fanfansann/fanfan-deep-learning-note/ 孩子的第一个 『Github』！给我个 $\boxed{⭐\text{Starred}}$ 嘛！谢谢！！o(〃＾▽＾〃)o

9）此属 version 1.0 ，若有错误，还需继续修正与增删，还望大家多多指点。本文会随着我的深入学习不断地进行完善更新，Github 中的 P D F 版也会尽量每月进行一次更新，所以建议点赞收藏分享加关注，以便经常过来回看！

如果觉得还不错或者能对你有一点点帮助的话，请帮我给本篇文章点个赞，你的支持是我创作的最大动力！^0^

要是没人点赞的话自然就更新慢咯 >_<

文章目录

• 《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础 （上）
• • 3.1 手写数字分类问题
  • • 3.1.1 手写数字图片数据集
    • 3.1.2 构建模型
    • 3.1.3 误差计算
    • 3.1.4 非线性模型
    • 3.1.4 手写数字图片识别实战
    • • 3.1.4.1 TensorFlow2.0 实现
      • 3.1.4.2 PyTorch 实现
  • 3.2 逻辑回归（Logistic Regression, LR）
  • • 3.2.1 决策边界
    • 3.2.2 逻辑回归模型
    • 3.2.3 代价函数
    • 3.2.4 优化方法

一文让你完全弄懂 信息论基础 与 softmax 回归实战《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础（下）目录：

    3.3 信息论基础
      3.3.1 信息论
      3.3.2 香农熵
      3.3.3 相对熵（KL 散度）
      3.3.4 交叉熵
      3.3.5 JS 散度
      3.3.6 Wasserstein 距离
      3.3.7 结构化概率模型
    3.4 Softmax 回归
      3.4.1 Softmax 回归模型
      3.4.2 优化方法
      3.4.3 权重衰减
      3.4.4 Fashion-MNIST 数据集图片分类实战
    3.5 Softmax 回归与逻辑回归的关系
      3.5.1 Softmax 回归与逻辑回归的关系
      3.5.2 多分类问题的 Softmax 回归与 k 个二元分类器
    3.6 面试问题集锦
    3.7 参考资料

本章话题 第 3 章（上）（点击即可跳转哟）：
话题 1 ：什么是分类问题？

《繁凡的深度学习笔记》第 3 章 分类问题与信息论基础 （上）

话题 1 ：什么是分类问题？

分类问题（classification），即找一个函数判断输入数据所属的类别，也即预测预测值属于某一段连续的实数区间的方法。分类问题可以是二类别问题（是 / 不是），也可以是多类别问题（在多种类别中判断输入数据具体属于哪一个类别）。与回归问题（regression）相比，分类问题的输出不再是连续值，而是离散值，用来指定其属于哪个类别。分类问题在现实中应用非常广泛，比如垃圾邮件识别，手写数字识别，人脸识别，语音识别等。

图源：[15]

  

  本章我们先从简单的多分类手写数字图片分类问题实战开始入手，使用 简单神经网络 解决分类问题，带大家切身体会一下分类问题的流程以及神经网络的魅力，我们将在第 6 章 神经网络与反向传播算法 中详细讲解神经网络，并使用诸如 通用逼近定理（universal approximation theorem）等理论来尝试说明神经网络为何如此强大。在体验完神经网络解决手写数字分类问题以后，我们将详细介绍机器学习中关于分类问题的线性分类器：解决二分类问题的 逻辑回归 以及由其拓展而来的解决多分类问题的 softmax 回归，理解和掌握这些理论，是机器学习的基础。

3.1 手写数字分类问题

3.1.1 手写数字图片数据集

  我们前面讲过机器学习是一种需要从数据中间学习的行为，因在解决机器学习问题之前我们需要先采集大量的真实样本数据 $(x,y)$ 。我们以手写的数字图片识别为例，如图 3.1 所示，我们需要收集大量的由真人书写的 $0\sim 9$​​ 的数字图片，为了便于存储和计算，一般把收集的原始图片缩放到某个固定的大小 (Size 或 Shape)，比如图片有 $224$​​ 个像素的行和 $224$​​ 个像素的列，则称图片大小为 $224\times 224$​​。我们将这张图片作为一组输入数据的 $x$​​。

图 3.1 手写数字图片示例

  

  同时，我们需要给每一张图片标注一个标签，也即图片的真实分类 $y$​​​​​ ，表明这张图片属于哪一个具体的类别，我们一般通过映射方式将类别名一一对应到从 $0$​​​​​ 开始编号的数字，比如说硬币的正反面，我们可以用 $0$​​​​​ 来表示硬币的反面，用 $1$​​​​​ 来表示硬币的正面，当然也可以反过来。这种编码方式叫作数字编码（Number Encoding）。手写数字图片识别问题编码则更为直观，我们直接使用数字的 $0\sim 9$​​​​​ 来表示类别名字为 $0\sim 9$​​​​​​ 的图片。

  如果希望模型能够在新样本上也能具有良好的表现，即模型泛化能力 （GeneralizationAbility）较好，那么我们应该尽可能多地增加数据集的规模和多样性（Variance），使得我们用于学习的训练数据集与真实的手写数字图片的分布（Ground-truth Distribution）尽可能的逼近，这样在训练数据集上面学到了模型能够很好的用于未见过的手写数字图片的预测。所以我们一般根据 $82$ 原则也即将数据集按照 $8:2$ 的比例拆分为训练集（Training Set）和测试集（Test Set）。

  机器学习的主要目的就是从训练集上学习到数据的真实模型，从而能够在未见过的测试集上也能够表现良好。为了确保我们量化一下模型在训练集和测试集上的表现，将其分别称为 训练误差 (training error) 和 测试误差 (test error) ，后者也经常称为 泛化误差 (generalization error) 。可以说，理想的模型就是在最小化训练误差的同时，最小化泛化误差。因此为了评估和测试各种算法的性能，不同问题下的统一且质量高的数据集必不可少。在手写数字图片识别问题下，Lecun, Bottou, Bengio, & Haffner 于 1998 年发布了名为 $\text{MNIST}$​​ 的手写数字图片数据集，它包含了 $0\sim 9$​​​ 共 $10$​​​ 种数字的手写图片，每种数字一共有 $7000$​​​ 张图片，采集自不同书写风格的真实手写图片，一共 $70000$​​​ 张图片。其中 $60000$​​​ 张图片作为训练集 ${\mathbb{D}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}$​​​ ，用来训练模型，剩下 $10000$​​​ 张图片作为测试集 ${\mathbb{D}}_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$​​​ ，用来测试模型的效果。训练集和测试集共同组成了整个 $\text{MNIST}$ 数据集 。

  考虑到手写数字图片包含的信息比较简单，每张数字图片均被缩放到了统一的 $28\times 28$ 的大小，同时只保留了灰度信息，如图 3.2 所示。这些图片由真人书写，包含了如字体大小、书写风格、粗细等丰富的样式，确保这些图片的分布与真实的手写数字图片的分布尽可能的接近，从而保证了模型的泛化能力。

图 3.2 MNIST手写数字图片示例   

  每张图片包含了 $h$​​​​​ 行（Height/Row）， $w$​​​​​ 列（Width/Column），每个位置保存了像素（Pixel）值，像素值一般使用 $0\sim 255$​​​​​ 的整形数值来表达颜色的强度信息，例如可以让 $0$​​​​​ 表示强度最低，$255$​​​​​ 表示强度最高。如果是彩色图片，则每个像素点包含了 R、G、B 三个通道的强度信息，分别代表三原色红、绿、蓝的红色通道、绿色通道、蓝色通道的颜色强度，所以与灰度图片不同，它的每个像素点使用一个 $1$​​​​​ 维、长度为 $3$​​​​​ 的向量（Vector） 来表示，向量的 $3$​​​​​ 个元素依次代表了当前像素点上面的 R、G、B 颜色强度，因此彩色图片需要保存为形状是 $[h,w,3]$​​​​​ 的张量（Tensor，可以理解为 $3$​​ 维数组）。如果是灰度图片，则直接使用一个数值来表示灰度强度即可。如图 3.3 所示，令 $0$​​​​​ 表示纯黑，$255$​​​​​ 表示纯白，因此它只需要一个形为 $[h,w]$​​​​​ 的二维矩阵（Matrix）来表示一张图片信息（当然也可以保存为 $[h,w,1]$​​​​​​ 形状的张量）。

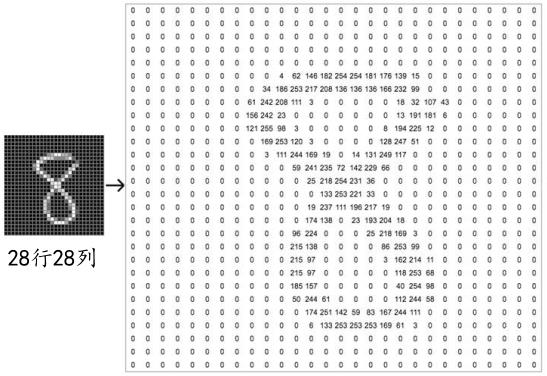
图 3.3 图的表示示意图   

3.1.2 构建模型

  回顾我们在回归问题讨论的生物神经元结构。我们把一组长度为 $d_{in}$​ 的输入向量 $\mathbf{x}=[x_1,x_2,\dots ,x_{d_{in}}{]}^{\mathrm{T}}$​ 简化为单输入标量 $x$​，模型可以表达成 $y=x\times w+b$​ 。如果是多输入、单输出的模型结构的话，我们需要借助于向量形式：

$$y={\mathbf{w}}^T\mathbf{x}+b=\left[w_1,w_2,w_3,\dots ,w_{d_{\mathrm{i}\mathrm{n}}}\right]\cdot \left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ \cdots \\ x_{d_{\mathrm{i}\mathrm{n}}}\end{array}\right]+b\text{\hspace{1em}(3.1)}$$

更一般地，通过组合多个多输入、单输出的神经元模型，可以拼成一个多输入、多输出的模型：
$$y=\mathbf{w}\cdot \mathbf{x}+b\text{\hspace{1em}(3.2)}$$

其中， x ∈ R d i n , b ∈ R d o u t , y ∈ R d o u t , W ∈ R d o u t × d i n \\boldsymbolx \\in R^d_\\mathrmi n, \\boldsymbolb \\in R^d_\\mathrmout, \\boldsymboly \\in R^d_\\mathrmout, W \\in R^d_\\mathrmout \\times d_\\mathrmi n 以上是关于分类问题与信息论基础（上）（DL笔记整理系列）的主要内容，如果未能解决你的问题，请参考以下文章

分类问题与信息论基础（上）（DL笔记整理系列）

分类问题与信息论基础（中）（DL笔记整理系列）

分类问题与信息论基础（中）（DL笔记整理系列）

分类问题与信息论基础（中）（DL笔记整理系列）

分类问题与信息论基础（中）（DL笔记整理系列）

回归问题与神经元模型（DL笔记整理系列）