2022天府杯数学建模A题 仪器故障智能诊断技术 总结及Python实现代码
Posted Better Bench
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022天府杯数学建模A题 仪器故障智能诊断技术 总结及Python实现代码相关的知识,希望对你有一定的参考价值。

1 题目
问题背景:
仪器设备故障诊断技术是一种了解和掌握机器在运行过程的状态,确定其整 体或局部正常或异常,早期发现故障及其原因,并能预报故障发展趋势的技术。仪器故障按照来源可分为外部型和内部型,其中外部型故障的产生多为静电放射、电磁辐射、雷暴天气、空气湿度过大等导致的电路损坏或传感器失灵,内部型故障多为齿轮破裂、电机短路等。油液监测、振动监测、噪声监测、性能趋势分析和无损探伤等为其主要的诊断技术方式。
随着计算机技术和人工智能科学的发展,基于机器学习或深度学习的故障智能诊断方法成为从业者的新型决策工具,其中故障类型识别是主要内容,该项技术特点在于:降低原始数据的环境噪声或异常数据影响,提取可靠的波形特征判据,选择或改进现有的机器学习方法,设计一系列必要的仿真实验,讨论与分析。
请解决:
(1) 针对附件一和附件二中的数据,各自由选择 1 条原始数据进行信号去
噪处理,并将处理效果汇总在附表 1-1 和附表 1-2 中,表中指标已存在 3 项,另
需参赛者添加至少 3 项评价指标,以完善故障数据去噪效果评价;
(2) 信号特征提取是进行故障智能检测的重要前提。请针对附件一和附件二中的全部数据进行信号的特征提取,特征判据数量不得少于 10 项,并将提取
的特征值汇总在附表 2-1 和附表 2-2 中;
(3) 基于无监督型或半监督型方法,进行附表 1 类数据和附表 2 类数据的
二分类实验,并将实验结果登记在附表 3 中,预测结果评价指标已存在 3 项,另
需参赛者添加至少 3 项评价指标,使用的预测方法应保证预测准确率均值在 90%
以上,准确率标准差在 10 以内;
(4) 基于有监督型学习方法,进行附表 1 类数据和附表 2 类数据的二分类
实验,并将实验结果登记在附表 4 中,预测结果评价指标已存在 3 项,另需参赛者另添加至少 3 项评价指标,使用的预测方法应保证预测准确率均值在 95%以上,准确率标准差在 5 以内;
2 问题一
2.1 问题解析
题目的意思是对信号进行去噪处理,可以采用小波去噪。小波变换方法又有不同的小波基,不同的小波基函数,是由同一个基本小波函数经缩放和平移生成的。
小波变换是将原始图像与小波基函数以及尺度函数进行内积运算,所以一个尺度函数和一个小波基函数就可以确定一个小波变换。
小波的不同小波基家族如下
haar家族: haar
db家族:
db1,db2,db3,db4,db5,db6,db7,db8,db9,db10,db11,db12,db13,db14,db15,db16,db17,db18,db19,db20,db21,db22,db23,db24,db25,db26,db27,db28,db29,db30,db31,db32,db33,db34,db35,db36,db37,db38
sym 家族: sym2,sym3,sym4,sym5,sym6,sym7,sym8,sym9,sym10,sym11,sym12,sym13,sym14,sym15,sym16,sym17,sym18,sym19,sym20
coif 家族: coif1,coif2,coif3,coif4,coif5,coif6,coif7,coif8,coif9,coif10,coif11,coif12,coif13,coif14,coif15,coif16,coif17
bior 家族: bior1.1,bior1.3,bior1.5,bior2.2,bior2.4,bior2.6,bior2.8,bior3.1,bior3.3,bior3.5,bior3.7,bior3.9,bior4.4,bior5.5,bior6.8
rbio 家族: rbio1.1,rbio1.3,rbio1.5,rbio2.2,rbio2.4,rbio2.6,rbio2.8,rbio3.1,rbio3.3,rbio3.5,rbio3.7,rbio3.9,rbio4.4,rbio5.5,rbio6.8
dmey家族: dmey
gaus 家族: gaus1,gaus2,gaus3,gaus4,gaus5,gaus6,gaus7,gaus8
mexh 家族: mexh
morl 家族: morl
cgau 家族: cgau1,cgau2,cgau3,cgau4,cgau5,cgau6,cgau7,cgau8
shan 家族: shan
fbsp 家族: fbsp
cmor 家族: cmor
2.2 python实现
使用python中的Pywt工具包进行小波变换去噪
参考
【Pywt讲解】https://blog.csdn.net/qq_40587575/article/details/83154042
【Pywt去噪例子】https://blog.csdn.net/weixin_50888378/article/details/111874677
# python实现
import numpy as np
import pywt
import pandas as pd
import matplotlib.pylab as plt
import warnings # Supress warnings
warnings.filterwarnings('ignore')
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
import numpy as np
import math
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# 输入S为纯信号,是一个numpy的1D张量
# 输入SN为带噪信号,是一个numpy的1D张量
# 输出snr为信噪比,单位为dB,是一个32为的float数
def SNR(SN, S):
# 其中S是纯信号,SN是带噪信号,snr是信噪比
Ps = sum((S-(np.mean(S)))**2) #signal power
Pn = sum((S-SN)** 2)# noise power
snr = 10*math.log((Ps/Pn), 10)
return(snr)
def print_metric(y_test, y_predict):
mse = mean_squared_error(y_test, y_predict)
mae = mean_absolute_error(y_test, y_predict)
mape = np.mean(np.abs((y_predict - y_test) / y_test)) * 100
r2 = r2_score(y_test, y_predict)
snr = SNR(y_test, y_predict)
rmse = np.sqrt(((y_predict - y_test) ** 2).mean())
sse = np.sum((y_test - y_predict) ** 2)
print('MSE: SSE: RMSE: SNR: MAE: MAPE: R2: '.format(mse, sse, rmse, snr, mae,mape, r2))
return [mse, sse, rmse, snr, mae, mape, r2]
阈值需要去调整的,这是一个超参数,不同阈值对于去噪效果不同。怎么去调整阈值,有很多文献去研究的。
file = 8
metric_list = []
obj = 'db9' # ['db3', 'db6', 'db9', 'bior2.2', 'rbio1.1', 'dmey']:
# Get data:
input_data = np.array(pd.read_csv(r"../data/.txt".format(file), sep=' ', header=None))
if file > 4:
ecg = input_data
else:
ecg = input_data.T
index = []
data = []
for i in range(ecg.shape[0]-1):
X = float(i)
Y = float(ecg[i])
index.append(X)
data.append(Y)
# 创建小波对象并定义参数:
w = pywt.Wavelet(obj) # 选用Daubechies8小波
maxlev = pywt.dwt_max_level(len(data), w.dec_len)
# print("maximum level is " + str(maxlev))
threshold = 0.10 # Threshold for filtering
# 分解为小波分量,直至选定的水平:
coeffs = pywt.wavedec(data, obj, level=maxlev) # 将信号进行小波分解
plt.figure()
for i in range(1, len(coeffs)):
coeffs[i] = pywt.threshold(
coeffs[i], threshold*max(coeffs[i])) # 将噪声滤波
datarec = pywt.waverec(coeffs, obj) # 将信号进行小波重构
mintime = 0
maxtime = mintime + len(data) + 1
print('-----------------------------'.format(obj))
tmplist = print_metric(ecg.reshape(-1,), datarec)
metric_list.append(tmplist)
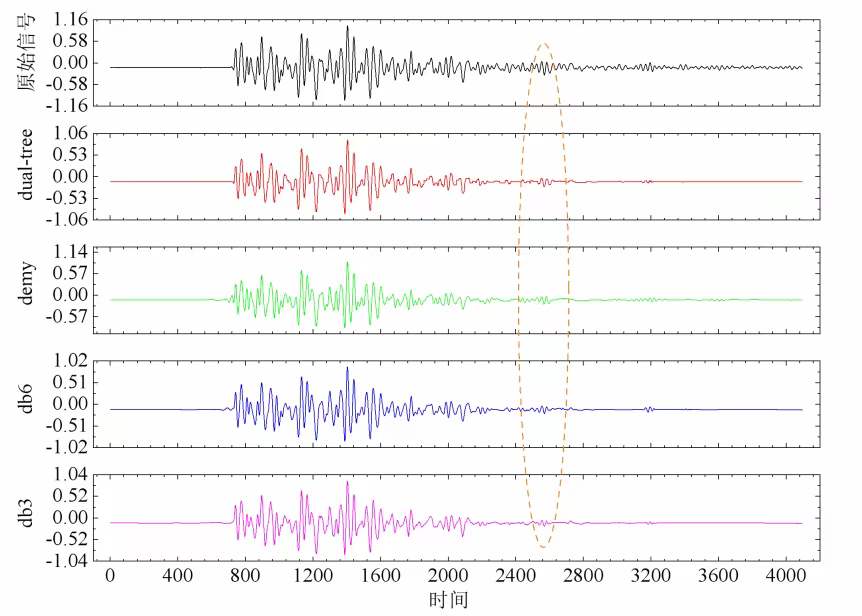
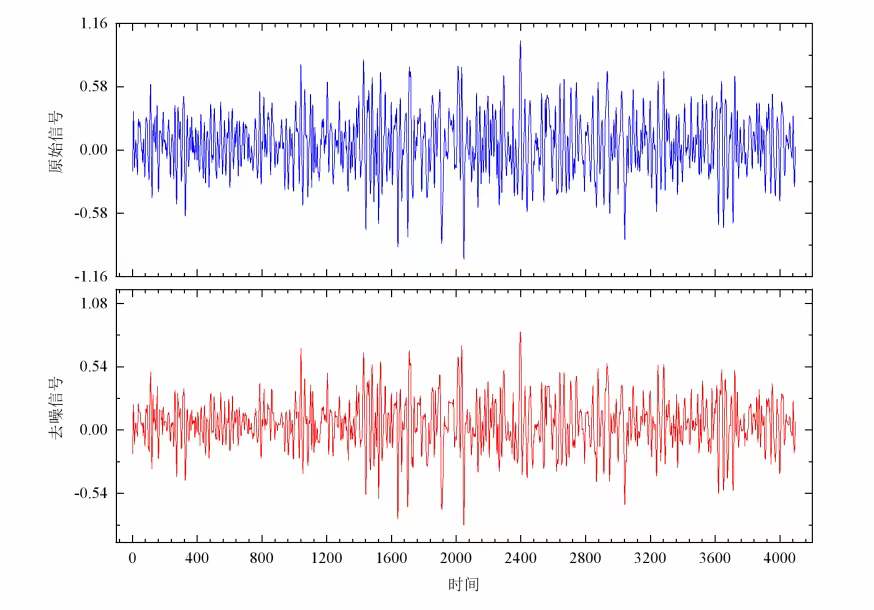
选择其中一个小波基的小波变换可视化代码实现如下
plt.figure()
plt.plot(index[mintime:maxtime], data[mintime:maxtime])
plt.plot(index[mintime:maxtime], datarec[mintime:maxtime-1])
plt.show()
3 问题二
3.1 问题分析
这是一个对实数信号进行特征工程的问题。需要对信号提取时域特征和频域特征。时域特征的方法公式如下所示

频域特征的方法公式如下所示

2.2 Python实现
直接读取信号
import pandas as pd
import warnings # Supress warnings
warnings.filterwarnings('ignore')
import numpy as np
data = []
for i in range(100):
filepath = "../data/.txt".format(i+1)
if i<70:
txt = pd.read_csv(filepath,sep=' ', header=None).T
else:
txt = pd.read_csv(filepath, sep=' ', header=None)
data.append(list(txt[0]))
x = np.array(data)
df = pd.DataFrame(data)
df.to_csv('../data/1-100.csv',index=0)
提取特征
import scipy.stats
class Fea_Extra():
def __init__(self, Fs=25600):
self.Fs = Fs
def Time_fea(self, signal_):
"""
提取时域特征 11 类
"""
N = len(signal_)
y = signal_
t_mean_1 = np.mean(y) # 1_均值(平均幅值)
t_std_2 = np.std(y, ddof=1) # 2_标准差
t_fgf_3 = ((np.mean(np.sqrt(np.abs(y)))))**2 # 3_方根幅值
t_rms_4 = np.sqrt((np.mean(y**2))) # 4_RMS均方根
# 5_峰峰值 (参考周宏锑师姐 博士毕业论文)
t_pp_5 = 0.5*(np.max(y)-np.min(y))
#t_skew_6 = np.sum((t_mean_1)**3)/((N-1)*(t_std_3)**3)
t_skew_6 = scipy.stats.skew(y) # 6_偏度 skewness
#t_kur_7 = np.sum((y-t_mean_1)**4)/((N-1)*(t_std_3)**4)
t_kur_7 = scipy.stats.kurtosis(
y) # 7_峭度 Kurtosis
# 8_峰值因子 Crest Factor
t_cres_8 = np.max(np.abs(y))/t_rms_4
# 9_裕度因子 Clearance Factor
t_clear_9 = np.max(np.abs(y))/t_fgf_3
t_shape_10 = (N * t_rms_4)/(np.sum(np.abs(y))
) # 10_波形因子 Shape fator
t_imp_11 = (np.max(np.abs(y))) / \\
(np.mean(np.abs(y))) # 11_脉冲指数 Impulse Fator
t_fea = np.array([t_mean_1, t_std_2, t_fgf_3, t_rms_4, t_pp_5,
t_skew_6, t_kur_7, t_cres_8, t_clear_9, t_shape_10, t_imp_11])
#print("t_fea:",t_fea.shape,'\\n', t_fea)
return t_fea
def Fre_fea(self, signal_):
"""
提取频域特征 13类
:param signal_:
:return:
"""
L = len(signal_)
PL = abs(np.fft.fft(signal_ / L))[: int(L / 2)]
PL[0] = 0
f = np.fft.fftfreq(L, 1 / self.Fs)[: int(L / 2)]
x = f
y = PL
K = len(y)
f_12 = np.mean(y)
f_13 = np.var(y)
f_14 = (np.sum((y - f_12)**3))/(K * ((np.sqrt(f_13))**3))
f_15 = (np.sum((y - f_12)**4))/(K * ((f_13)**2))
f_16 = (np.sum(x * y))/(np.sum(y))
f_17 = np.sqrt((np.mean(((x - f_16)**2)*(y))))
f_18 = np.sqrt((np.sum((x**2)*y))/(np.sum(y)))
f_19 = np.sqrt((np.sum((x**4)*y))/(np.sum((x**2)*y)))
f_20 = (np.sum((x**2)*y))/(np.sqrt((np.sum(y))*(np.sum((x**4)*y))))
f_21 = f_17/f_16
f_22 = (np.sum(((x - f_16)**3)*y))/(K * (f_17**3))
f_23 = (np.sum(((x - f_16)**4)*y))/(K * (f_17**4))
#f_24 = (np.sum((np.sqrt(x - f_16))*y))/(K * np.sqrt(f_17)) # f_24的根号下出现负号,无法计算先去掉
#print("f_16:",f_16)
#f_fea = np.array([f_12, f_13, f_14, f_15, f_16, f_17, f_18, f_19, f_20, f_21, f_22, f_23, f_24])
f_fea = np.array([f_12, f_13, f_14, f_15, f_16, f_17,
f_18, f_19, f_20, f_21, f_22, f_23])
#print("f_fea:",f_fea.shape,'\\n', f_fea)
return f_fea
def Both_Fea(self, signal_):
"""
:return: 时域、频域特征 array
"""
t_fea = self.Time_fea(signal_)
f_fea = self.Fre_fea(signal_)
fea = np.append(np.array(t_fea), np.array(f_fea))
#print("fea:", fea.shape, '\\n', fea)
return fea
主函数,提取特征后并将矩阵存储为csv文件,作为后续的机器学习的模型输入。
data = np.array(pd.read_csv('../data/1-100.csv'))
pro_data = []
fe = Fea_Extra()
for i in range(len(data)):
tmp_f = fe.Both_Fea(data[i])
pro_data.append(tmp_f)
clear_data = pd.DataFrame(np.array(pro_data))
clear_data.to_csv('./data/clear_data.csv',index=0)
4 问题三
4.1 问题分析
这是一个聚类问题,采用kmeans++聚类,K值为2,对附件一的数据标签编码为0,附件二的数据标签编码为1。
评价指标有准确率、召回率、F值、精确率、CH分数、轮廓系数、耗时

4.2 Python实现
from sklearn.metrics import precision_score
from sklearn.metrics import roc_auc_score
from sklearn.metrics import f1_score
import time
from sklearn.metrics import recall_score
from sklearn.metrics import accuracy_score
from sklearn.metrics import f1_score, precision_score, recall_score
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score
import numpy as np
def print_precison_recall_f1(y_true, y_pred):
# 准确率
acc = accuracy_score(y_true, y_pred)
# 召回率
recall = recall_score(y_true, y_pred, average='macro')
# F值
f1 = f1_score(y_true, y_pred, average='macro')
# CH分数
auc = roc_auc_score(y_true, y_pred)
# 精准率
p = precision_score(y_true, y_pred, average='macro')
# CH分数
ch = calinski_harabasz_score(np.array(y_true).reshape(-1,1), np.array(y_pred).reshape(-1,1))
print("ACC: Recall: f1: AUC: Precision: CH: ".format(acc, recall,f1,auc,p,ch))
return [acc, recall, f1, auc, p,ch]
kmeans++聚类
from sklearn.cluster import KMeans,MiniBatchKMeans,AgglomerativeClustering,Birch
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
data = pd.read_csv('./data/clear_data.csv')
time_start=time.time()
# 更改这里就行
clf0 = KMeans(n_clusters=2, random_state=2016)
time_end=time.time()
pred0 = clf0.fit_predict(data)
sil = silhouette_score(data, clf0.labels_, metric='euclidean')
# print("轮廓系数",sil)
Y = 70*[0]+30*[1]
print_precison_recall_f1(Y,pred0)
# 耗时
print('耗时: ',time_end-time_start,'s')
pca = PCA(n_components=3) # 输出两维
newData0 = pca.fit_transform(data) # 载入N维
x1, y1, z1 = [], [], []
x2, y2, z2 = [], [], []
x3, y3, z3 = [], [], []
for index, value in enumerate(pred0):
if value == 0:
x1.append(newData0[index][0])
y1.append(newData0[index][1])
z1.append(newData0[index][2])
elif value == 1<以上是关于2022天府杯数学建模A题 仪器故障智能诊断技术 总结及Python实现代码的主要内容,如果未能解决你的问题,请参考以下文章