解题报告力扣 第 74 场双周赛
Posted 英雄哪里出来
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了解题报告力扣 第 74 场双周赛相关的知识,希望对你有一定的参考价值。
文章目录
一、将数组划分成相等数对
1、算法:排序
先排序,然后隔位判断是否和相邻的数相等,不相等返回false;遍历完毕,都相等的话,返回true。
2、源码
class Solution
public:
bool divideArray(vector<int>& nums)
if(nums.size() & 1)
return false;
sort(nums.begin(), nums.end());
for(int i = 0; i < nums.size(); i += 2)
if(nums[i] != nums[i+1])
return false;
return true;
;
二、字符串中最多数目的子字符串
1、算法:贪心 + 前缀和(后缀和)
1)如果不进行插入
包含 pattern的子序列的个数是多少?
计算以
i
i
i 为后缀的字符串中,pattern[1]的个数有多少个,放入 post[i]中,枚举一个值为 pattern[0]的位置
i
i
i,把 post[i+1]加入到答案里。
2)如果进行插入
pattern[0]插入
−
1
-1
−1 的位置一定是最优的,则只需要统计串中 pattern[1]的个数 就是包含插入字符的子序列个数;
pattern[1]插入
n
n
n 的位置一定是最优的, 则只需要统计串中 pattern[0]个数 就是包含插入字符的子序列的个数;
两者选其优,也就是选择个大者和 不进行插入 的情况进行加和,就是答案了。
2、源码
long long maximumSubsequenceCount(char * text, char * pattern)
int post[100010], pattern0 = 0;
int i, len = strlen(text);
long long s = 0;
post[len] = 0;
for(i = len-1; i >= 0; --i)
post[i] = post[i+1] + ( text[i] == pattern[1] ? 1 : 0 );
for(i = 0; i < len; ++i)
if(text[i] == pattern[0])
s += post[i+1];
++pattern0;
s += post[0] > pattern0 ? post[0] : pattern0;
return s;
三、将数组和减半的最少操作次数
1、算法:贪心 + 大顶堆
每次从容器中选择一个最大值,并且减半以后再塞回容器,累加所有取出来的元素的值,如果满足条件则跳出循环。
容易想到,如果每次取最大的进行减半,一定是最优的。所以,问题就转变成了要求实现一个容器,能够 快速选取最大值、快速插入、快速删除。于是我们就想到了大顶堆。
然后就是直接用 C++ 的现成的容器 priority_queue啦。
2、源码
class Solution
public:
int halveArray(vector<int>& nums)
long long s = 0;
int ans = 0;
priority_queue <double> q;
for(int i = 0; i < nums.size(); ++i)
s += nums[i];
q.push(nums[i]);
double tar = s / 2.0;
while(!q.empty())
double top = q.top();
q.pop();
tar -= top / 2;
++ans;
if(tar <= 0)
break;
q.push(top / 2);
return ans;
;
四、用地毯覆盖后的最少白色砖块
1、算法:动态规划
1)设计状态
我们来看,面对这样一道题,我们怎么去设计状态呢?
首先看它的数据量,地板的长度和地毯的长度都为
1000
1000
1000,很容易想到是一个
1000
×
1000
1000 \\times 1000
1000×1000 的算法,比如 地板长度为
n
n
n,地毯长度为
m
m
m。算法的时间复杂度应该为
O
(
n
×
m
)
O(n \\times m)
O(n×m)。

2)设计状态转移方程
能够想到用
i
i
i 地毯来铺
j
j
j 块地板的状态定义为
(
i
,
j
)
(i, j)
(i,j),那么可以分为两种情况:一个是第
j
j
j 块地板没有地毯的情况,一个是第
j
j
j 块地板有地毯的情况。
所以我们令:
d
p
[
0
]
[
i
]
[
j
]
dp[0][i][j]
dp[0][i][j] 代表用了
i
i
i 块地毯,第
j
j
j 块地板没有地毯的情况;
d
p
[
1
]
[
i
]
[
j
]
dp[1][i][j]
dp[1][i][j] 代表用了
i
i
i 块地毯,第
j
j
j 块地板有地毯的情况;
3)状态转移
由于状态已经达到 1 0 6 10^6 106 的量级了,所以状态转移的时间复杂度只能是 O ( 1 ) O(1) O(1)( O ( l o g n ) O(logn) O(logn) 不一定可以,也不一定不可以,看数据卡不卡你),所以,大概率情况下,我们还是要用 O ( 1 ) O(1) O(1) 的思想去思考状态如何转移。
3.a) d p [ 0 ] [ i ] [ j ] dp[0][i][j] dp[0][i][j]
d
p
[
0
]
[
i
]
[
j
]
dp[0][i][j]
dp[0][i][j] 代表用了
i
i
i 块地毯,第
j
j
j 块地板没有地毯的情况;那么,它的前一块地板有可能有地毯(
d
p
[
1
]
[
i
]
[
j
−
1
]
dp[1][i][j-1]
dp[1][i][j−1]),也有可能没有地毯(
d
p
[
0
]
[
i
]
[
j
−
1
]
dp[0][i][j-1]
dp[0][i][j−1])。
由于第
j
j
j 块地板它没有地毯,就要加上floor[j] - '0'个白色方块。
于是,状态转移方程就是:
d
p
[
0
]
[
i
]
[
j
]
=
m
i
n
(
d
p
[
0
]
[
i
]
[
j
−
1
]
,
d
p
[
1
]
[
i
]
[
j
−
1
]
)
+
f
l
o
o
r
[
j
]
−
′
0
′
dp[0][i][j] = min(dp[0][i][j-1], dp[1][i][j-1]) + floor[j] - '0'
dp[0][i][j]=min(dp[0][i][j−1],dp[1][i][j−1])+floor[j]−′0′
3.b) d p [ 1 ] [ i ] [ j ] dp[1][i][j] dp[1][i][j]
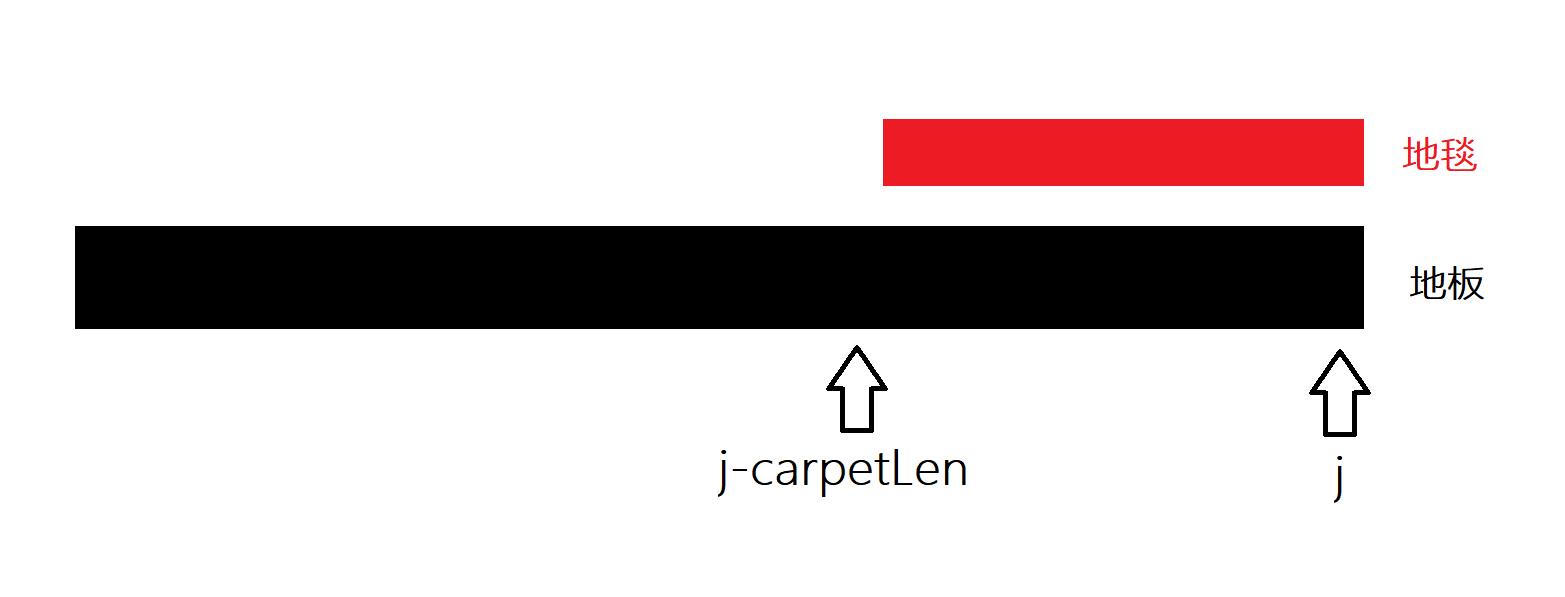
d p [ 1 ] [ i ] [ j ] dp[1][i][j] dp[1][i][j] 代表用了 i i i 块地毯,第 j j j 块地板有地毯的情况;那么一定是在当前的这块地板上放了一个地毯,则它的状态一定是从 d p [ 0 ] [ i − 1 ] [ j − c a r p e t L e n ] dp[0][i-1][j-carpetLen] dp[0][i−1][j−carpetLen] 和 d p [ 1 ] [ i − 1 ] [ j − c a r p e t L e n ] dp[1][i-1][j-carpetLen] dp[1][i−1][j−carpetLen] 中的小者转移过来。
4)初始状态
4.a) i = 0 , d p [ 0 ] [ 0 ] [ j ] i = 0,dp[0][0][j] i=0,dp[0][0][j]
d p [ 0 ] [ 0 ] [ j ] dp[0][0][j] dp[0][0][j] 代表了用了 0 个地毯,到第 j j j 块地板上,最少的白色块的数目,那么它就是 f l o o r floor floor 的前缀和。
4.b) i = 0 , d p [ 1 ] [ 0 ] [ j ] i = 0,dp[1][0][j] i=0,dp[1][0][j]
这是一个什么状态?
这是非法的,因为它矛盾了,第一维代表至少要一个地毯,而第二维只有 0 个地毯,所以不同维度的状态之间产生矛盾,是一个非法状态。
5)特殊状态
为了让地毯不重叠,那么地毯在覆盖的时候,势必会遇到一个问题。什么问题呢?
地毯一定有可能会出界,所以一定会有一些
j
<
0
j < 0
j<0 的状态
d
p
[
0
]
[
i
]
[
j
]
dp[0][i][j]
dp[0][i][j] 是合法的。
合法状态就是:
d
p
[
0
]
[
0
]
[
j
]
=
0
(
j
<
0
)
dp[0][0][j] = 0 \\ \\ (j < 0)
dp[0以上是关于解题报告力扣 第 74 场双周赛的主要内容,如果未能解决你的问题,请参考以下文章