[硫化铂]移花接木
Posted StaroForgin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[硫化铂]移花接木相关的知识,希望对你有一定的参考价值。
移花接木
题目概述

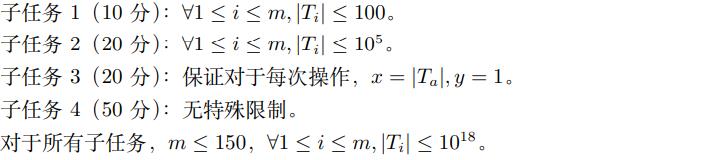
题解
首先,由于我们的
∣
T
i
∣
|T_i|
∣Ti∣可能达到
1
0
18
10^18
1018,所以显然我们不可能对于所有的点都去,显然,我们是只会维护一部分关键点的。
由于在树上我们有结论,到一个点最远的点中必然有一个点是直径的两端点之一。
那么我们只需要找到这两个直径的端点,算这两个点到直径中点两侧别的点的距离和就行。
如何在合并两棵树时,求新树的直径?
从上面的结论可以发现,我们新形成的直径端点一定是原来直径的端点。
那么我们可以将原来的直径自由组合,得到新的直径。
显然,在这种情况下,在某一层我们会真正参与递归的点必然是从后面的层传递下来的或者本层的分割点与直径端点。
这也就说明我们的总点数是
O
(
m
)
O\\left(m\\right)
O(m)的。
那么我们这部分的时间复杂度应该是
O
(
m
3
)
O\\left(m^3\\right)
O(m3)。
在求出直径后,我们又该怎么计算我们的答案呢?
我们不妨假设我们我们的直径长度为
L
L
L,先考虑
L
L
L为奇数的情况。
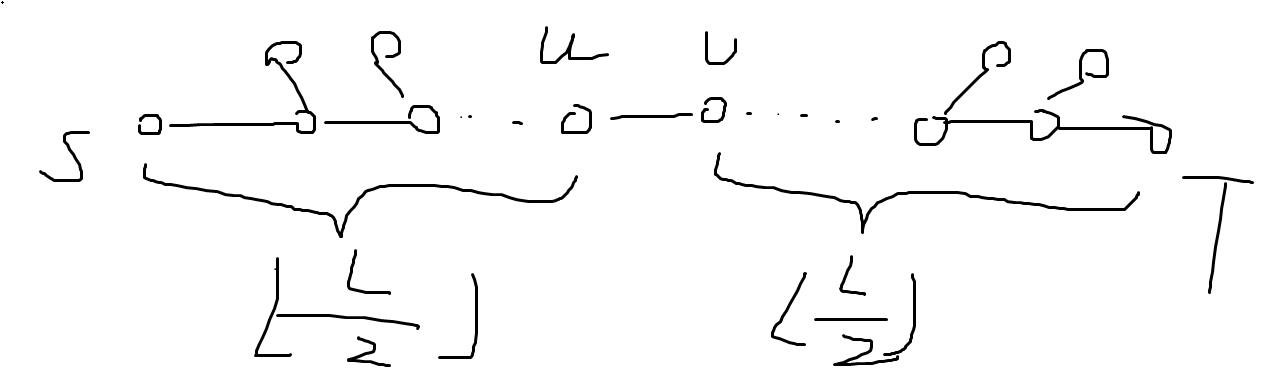
显然可以发现,右侧的点都是到
S
S
S最优,左侧的点都是到
T
T
T最优。
我们可以尝试从
S
S
S走到
v
v
v,统计
v
v
v子树内所有点到
v
v
v的路径长度和,从
T
T
T走到
u
u
u,统计
u
u
u子树内所有点到
u
u
u的路径长度和。
相当于让所有点走到了自己对应的
u
/
v
u/v
u/v,之后就再让它们走到
T
/
S
T/S
T/S就行了,显然之后的路径长度是
⌈
L
2
⌉
\\lceil\\fracL2\\rceil
⌈2L⌉。
那么我们需要计算的就是在树
i
i
i内以
r
t
rt
rt为根,向点
x
x
x的方向走
d
d
d步所到点的子树内所有点的距离和,我们记为
F
i
(
r
t
,
x
,
d
)
F_i(rt,x,d)
Fi(rt,x,d)。
显然其转移也可以像我们上面一样记忆化递归求解,同样它的状态数也是比较少的,但是转移要看
r
t
,
x
rt,x
rt,x与割点的位置关系来转移。
不同的位置关系有
4
4
4种:
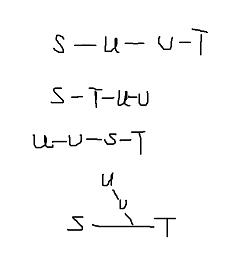
- u − v u-v u−v能够将 S − T S-T S−T分隔开,显然此时只需要考虑我们走 d d d步关于 u − v u-v u−v的位置就能继续递归下去。
- u − v u-v u−v在 T T T的子树内,那么我们分割后的另一子树一定会被统计到 F F F内去,继续递归。
- u − v u-v u−v在 S S S的另一子树内,必然不可能被统计入答案,继续递归。
- u − v u-v u−v从 S − T S-T S−T的路径分叉出去,这种情况要依据 d d d的大小,判断该子树能否统计入答案,继续递归。
至于如何判断属于哪种情况,我们可以通过
d
i
s
(
s
,
u
)
,
d
i
s
(
s
,
t
)
,
d
i
s
(
t
,
u
)
dis(s,u),dis(s,t),dis(t,u)
dis(s,u),dis(s,t),dis(t,u)三个量互相之间的大小关系判断。
这三个量可以用我们上面求直径的方式递归求出。
然后,我们就可以记忆化
d
p
dp
dp求出我们的答案了。
于是当
L
L
L为奇数的答案为:
A
n
s
i
=
F
i
(
S
,
T
,
⌈
L
2
⌉
)
+
F
i
(
T
,
S
,
⌈
L
2
⌉
)
+
⌈
L
2
⌉
∣
T
i
∣
Ans_i=F_i(S,T,\\lceil\\fracL2\\rceil)+F_i(T,S,\\lceil\\fracL2\\rceil)+\\lceil\\fracL2\\rceil|T_i|
Ansi=Fi(S,T,⌈2L⌉)+Fi(T,S,⌈2L⌉)+⌈2L⌉∣Ti∣
那么之后我们考虑我们
L
L
L为偶数的又是怎样的一个情况。
如图:
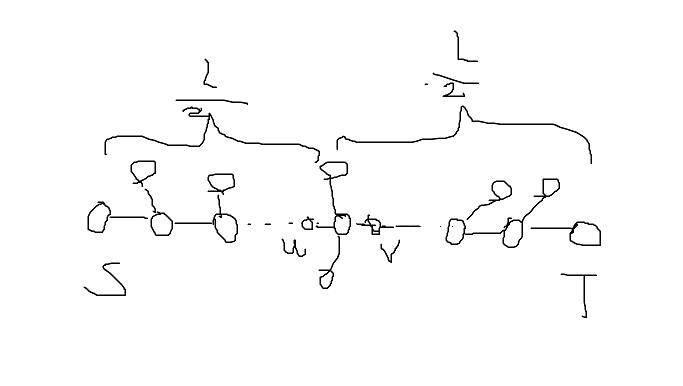
其中,我们
u
u
u的子树与
v
v
v的子树是仍然可以按我们上面的求出,但此时我们
u
,
v
u,v
u,v中间点就不能这样了,因为它之后需要走的路径比
u
,
v
u,v
u,v小
1
1
1,也就是说我们最后不能像
⌈
L
i
2
⌉
∣
T
i
∣
\\lceil\\fracL_i2\\rceil|T_i|
⌈2Li⌉∣Ti∣这样直接加起来,我们还需要计算一下两边子树内的节点数。
我们不妨直接把中间的点归入一侧,只是两侧的距离不一样罢了。
我们记
G
i
(
r
t
,
x
,
d
)
G_i(rt,x,d)
Gi(rt,x,d)表示在第
i
i
i棵树内,以点
r
t
rt
rt为根,向点
x
x
x走
d
d
d步,到的点的子树内的节点数。
这依然可以像我们上面求
F
F
F一样,递归求出,甚至还要更加简单。
可以得到,
L
L
L为偶数时,我们的答案为:
A
n
s
i
=
F
i
(
S
,
T
,
⌊
L
2
⌋
)
+
F
i
(
T
,
S
,
⌊
L
2
⌋
+
1
)
+
⌊
L
2
⌋
∣
T
i
∣
+
G
i
(
T
,
S
,
L
2
+
1
)
Ans_i=F_i(S,T,\\lfloor\\fracL2\\rfloor)+F_i(T,S,\\lfloor\\fracL2\\rfloor+1)+\\lfloor\\fracL2\\rfloor |T_i|+G_i(T,S,\\fracL2+1)
Ansi=Fi(S,T,⌊2L⌋)+Fi(T,S,⌊2L⌋+1)+⌊2L⌋∣Ti∣+Gi(T,S,2L+1)具体做法与上面的一样。
另外要注意的一点是,由于我们的
F
i
(
x
,
y
,
0
)
F_i(x,y,0)
Fi(x,y,0)这样的可能会多种
y
y
y不一样的情况,但实际上算的都是整棵树的情况,对于这种我们不如直接记忆化
F
i
(
x
,
x
,
0
)
F_i(x,x,0)
Fi(x,x,0),这样方便点。
当然,这种情况由于要覆盖整棵树,与上面的四种情况实际上是不太一样的,递归时也要单独讨论。
时间复杂度 O ( m 3 ) O\\left(m^3\\right) O(m3),但由于我用了 m a p map map来维护点新的编号实际上是