翻译: 深入神经网络 2.4. 微积分 pytorch

Posted 2022-03-15 AI架构师易筋

直到至少 2500 年前，当古希腊人将多边形划分为三角形并求和它们的面积时，找到多边形的面积仍然是个谜。为了找到弯曲形状（例如圆形）的面积，古希腊人在这种形状中刻上多边形。如图2.4.1所示 ，具有更多等长边的内接多边形更接近于圆。这个过程也被称为穷举法。

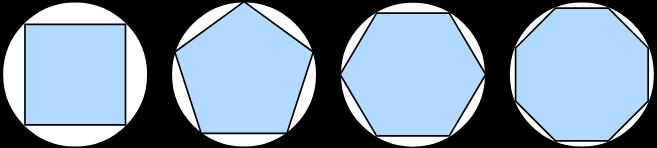
图 2.4.1用穷举法求圆的面积。

事实上，穷举法是积分学（将在第 18.5 节中描述）的起源。2000 多年后，微积分的另一个分支——微积分被发明了。在微积分最关键的应用中，优化问题考虑了如何做最好的事情。如 第 2.3.10.1 节所述，此类问题在深度学习中无处不在。

在深度学习中，我们训练模型，不断更新它们，以便它们在看到越来越多的数据时变得越来越好。通常，变得更好意味着最小化损失函数，这个分数回答了“我们的模型有多糟糕？”这个问题。这个问题比看起来更微妙。最终，我们真正关心的是生成一个在我们以前从未见过的数据上表现良好的模型。但是我们只能将模型拟合到我们实际可以看到的数据。因此，我们可以将拟合模型的任务分解为两个关键问题：

• （i）optimization优化训练：将我们的模型拟合到观察数据的过程；
• (ii)generalization 一般化预测：指导如何生成模型的数学原理和从业者的智慧，其有效性超出了用于训练它们的确切数据示例集。

为了帮助您在后面的章节中理解优化问题和方法，我们在此简要介绍深度学习中常用的微积分。

2.4.1 偏导数

我们首先解决导数的计算问题，这是几乎所有深度学习优化算法中的关键步骤。在深度学习中，我们通常选择相对于模型参数可微的损失函数。简而言之，这意味着对于每个参数，我们可以确定损失会以多快的速度增加或减少，如果我们以无限小的量增加或减少该参数。

%matplotlib inline
import numpy as np
from IPython import display
from d2l import torch as d2l


def f(x):
    return 3 * x ** 2 - 4 * x

def numerical_lim(f, x, h):
    return (f(x + h) - f(x)) / h

h = 0.1
for i in range(5):
    print(f'h=h:.5f, numerical limit=numerical_lim(f, 1, h):.5f')
    h *= 0.1

h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003

def use_svg_display():  #@save
    """Use the svg format to display a plot in Jupyter."""
    display.set_matplotlib_formats('svg')

我们定义set_figsize函数来指定图形大小。注意这里我们直接使用，因为在前言中已经d2l.plt将import语句 标记为保存在包中。

def set_figsize(figsize=(3.5, 2.5)):  #@save
    """Set the figure size for matplotlib."""
    use_svg_display()
    d2l.plt.rcParams['figure.figsize'] = figsize

以下set_axes函数设置由 生成的图形轴的属性matplotlib。

#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
    """Set the axes for matplotlib."""
    axes.set_xlabel(xlabel)
    axes.set_ylabel(ylabel)
    axes.set_xscale(xscale)
    axes.set_yscale(yscale)
    axes.set_xlim(xlim)
    axes.set_ylim(ylim)
    if legend:
        axes.legend(legend)
    axes.grid()

使用这三个图形配置函数，我们定义了 plot简洁地绘制多条曲线的函数，因为我们需要在整本书中可视化许多曲线。

#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None,
         ylim=None, xscale='linear', yscale='linear',
         fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
    """Plot data points."""
    if legend is None:
        legend = []

    set_figsize(figsize)
    axes = axes if axes else d2l.plt.gca()

    # Return True if `X` (tensor or list) has 1 axis
    def has_one_axis(X):
        return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
                and not hasattr(X[0], "__len__"))

    if has_one_axis(X):
        X = [X]
    if Y is None:
        X, Y = [[]] * len(X), X
    elif has_one_axis(Y):
        Y = [Y]
    if len(X) != len(Y):
        X = X * len(Y)
    axes.cla()
    for x, y, fmt in zip(X, Y, fmts):
        if len(x):
            axes.plot(x, y, fmt)
        else:
            axes.plot(y, fmt)
    set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)

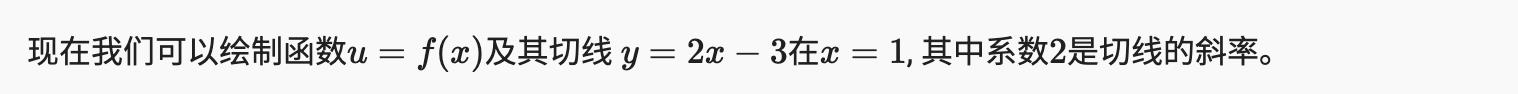
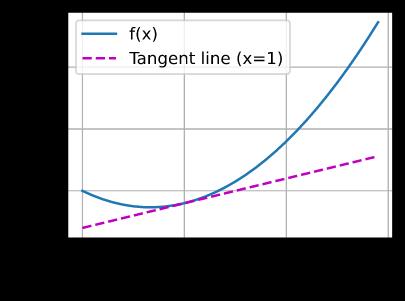
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

2.4.2. 偏导数

到目前为止，我们只处理了一个变量的函数微分。在深度学习中，函数通常依赖于许多变量。因此，我们需要将微分的思想扩展到这些 多元函数。

2.4.3。渐变

2.4.4 链式法则

2.4.5 概括

• 微积分和积分是微积分的两个分支，前者可以应用于深度学习中无处不在的优化问题。

• 导数可以解释为函数相对于其变量的瞬时变化率。它也是函数曲线的切线斜率。

• 梯度是一个向量，其分量是多元函数对其​​所有变量的偏导数。

• 链式法则使我们能够区分复合函数。

2.4.6练 习

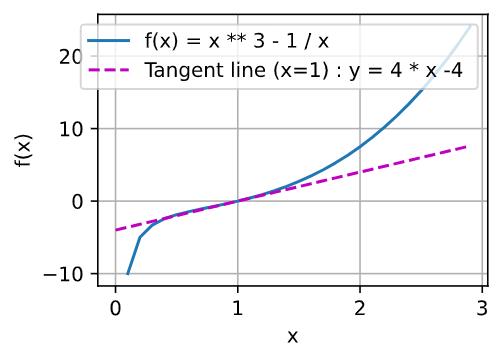
x = np.arange(0, 3, 0.1)
plot(x, [x ** 3 - 1 / x, 4 * x - 4], 'x', 'f(x)', legend=['f(x) = x ** 3 - 1 / x ', 'Tangent line (x=1) : y = 4 * x - 4 '])

参考

https://d2l.ai/chapter_preliminaries/calculus.html