3-4 k近邻算法 kd树的原理与改进

Posted 2022-03-12 windmissing

构造

KD树的构造过程实际上是用许多与坐标轴平行的分割线按照一定规划将一个空间划分成多个子空间。

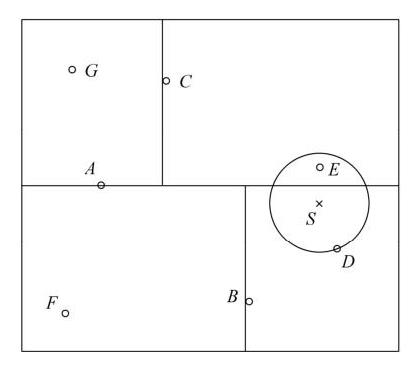
其中，每个分割线都经过一个样本点，每个区域有一个样本点。
将上图这样的划分转换成的kd树是：

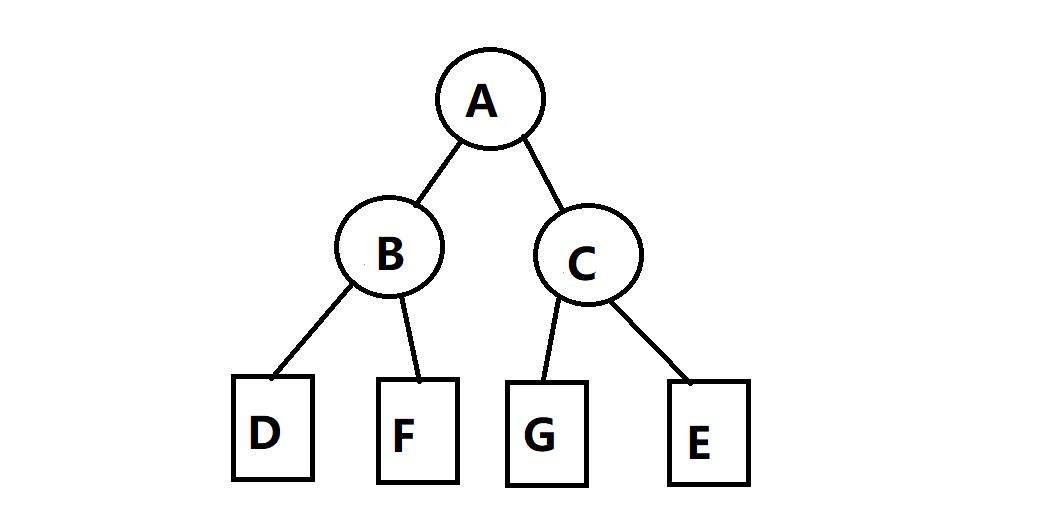
其中，圆形结点代表分割线上的样本，方形结点代表区域中的样本。

可以发现，方形结点所在的区域是由它的路径上的圆形结点所在的分割线分割出来的。
例如：
D所在的区域是经过A、B所在的分割线切割得到的。
E所在的区域是经过A、C所在的分割线切割得到的。

搜索

KD的树的优化策略是省去对大部分数据点的搜索，从而减少搜索的计算量。

假设目标点落在与D相同的区域，那么应该在以下这些点中搜索来寻找最近点：

	所在的位置	点	个数
1	与目标点同区域的点	D	1
2	目标点所在区域的分界线上的点	A、B	$${\log }_{2}N-1$$
3	分界线的另一侧区域的点	A所在分界线的另一侧区域的点：C、E、G B所在分界线的另一侧区域的点：F	$$2^1-1+2^2-1+\cdots$$

1类点和2类点的数量比较少，剪枝优化主要是针对3类点进行的。
只有在目标点离分界线足够近的情况下，才会考虑搜索分界线另一侧区域的点。
判断依据为：目标点到边界的距离 < 当前记录的最近距离。
如果条件不符合，分界线另一侧所有的点都不用搜索了，相当于一次砍掉了半棵子树，这个优化还是比较可观的。

升级成K近邻

书上算法为寻找最近邻。
每次寻找对最近邻后，将这个最近邻mark一下。
并令所有被mark过的点到目标点的距离为inf。