leetcode困难剑指 Offer 51数组中的逆序对

Posted 2022-03-09 qq_40707462

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

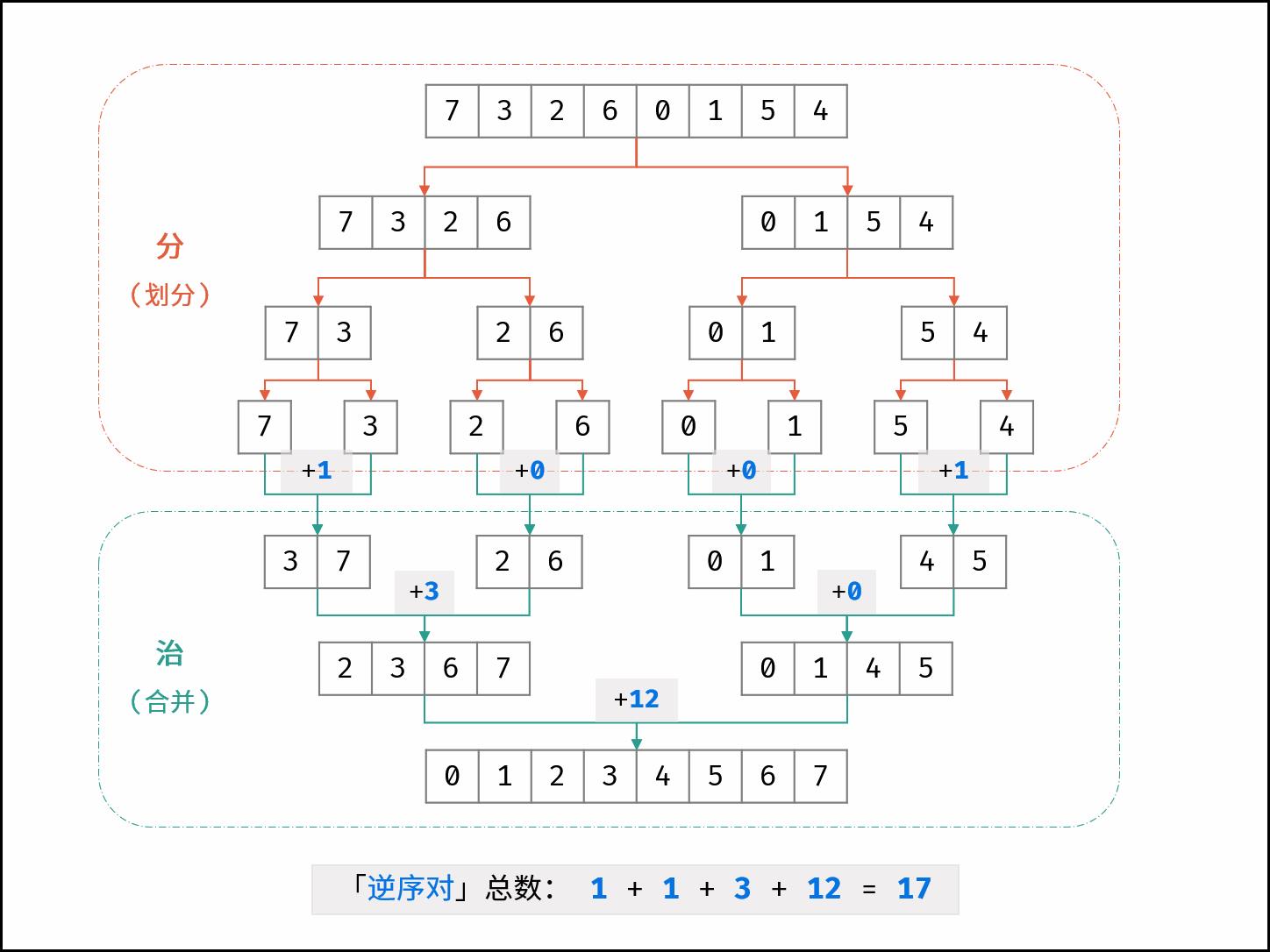
思路1、归并

时间复杂度O(NlogN)
空间复杂度 O(N) 辅助数组 tmp

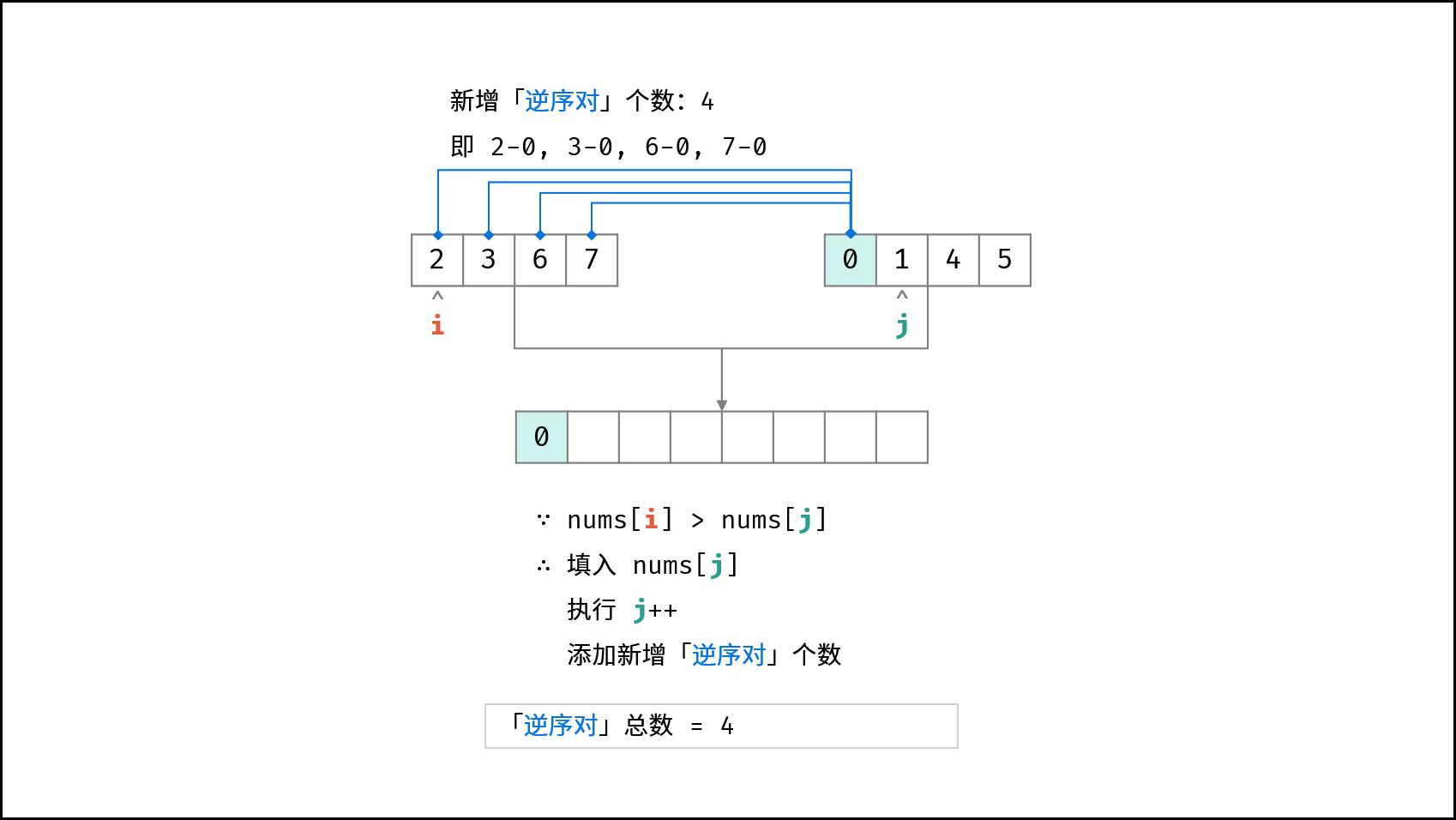
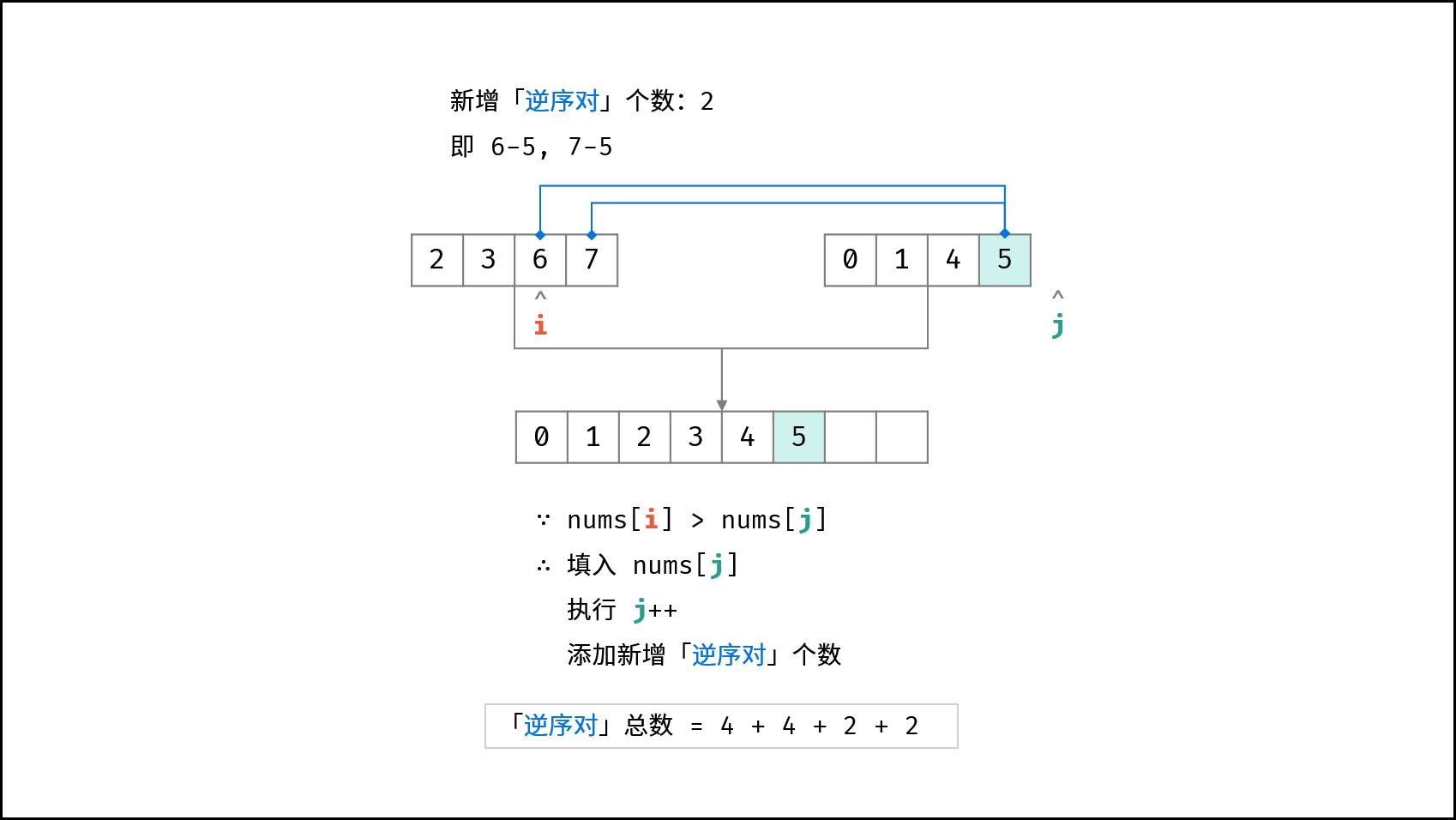
每当遇到 左子数组当前元素 > 右子数组当前元素 时，意味着 「左子数组当前元素 至 末尾元素」 与 「右子数组当前元素」 构成了若干 「逆序对」

在归并排序中，边排序，边计算遇到逆序的个数

两两合并示例：


总流程：

public class Solution 
    int count;
    public int reversePairs(int[] nums) 
        this.count = 0;
        merge(nums, 0, nums.length - 1);
        return count;
    

    public void merge(int[] nums, int left, int right) 
        int mid = left + ((right - left) >> 1);
        if (left < right) 
            merge(nums, left, mid);
            merge(nums, mid + 1, right);
            mergeSort(nums, left, mid, right);
        
    

    public void mergeSort(int[] nums, int left, int mid, int right) 
        int[] temparr = new int[right - left + 1];//两数组合并依次移入temp
        int index = 0;
        int temp1 = left, temp2 = mid + 1;

        while (temp1 <= mid && temp2 <= right) 
            if (nums[temp1] <= nums[temp2]) 
                temparr[index++] = nums[temp1++];
             else 
                //用来统计逆序对的个数
                count += (mid - temp1 + 1);
                temparr[index++] = nums[temp2++];
            
        
        //把左边剩余的数移入数组
        while (temp1 <= mid) 
            temparr[index++] = nums[temp1++];
        
        //把右边剩余的数移入数组
        while (temp2 <= right) 
            temparr[index++] = nums[temp2++];
        
        //把新数组中的数覆盖nums数组
        for (int k = 0; k < temparr.length; k++) 
            nums[k + left] = temparr[k];
        
    

思路2、树状数组

树状数组是一种可以动态维护序列前缀和的数据结构，它的功能是：

• 单点更新 update(i, v)： 把序列 i 位置的数加上一个值 v，这题 v = 1
• 区间查询 query(i)： 查询序列[1⋯i] 区间的区间和，即 i 位置的前缀和
• 修改和查询的时间代价都是O(logn)，其中 nn 为需要维护前缀和的序列的长度。

假设a=5,5,2,3,6，用一个桶记录这些数字出现的次数如下，第 i−1 位的前缀和表示「有多少个数比 i 小」

index  ->  1 2 3 4 5 6 7 8 9
value  ->  0 1 1 0 2 1 0 0 0

1. 从后往前遍历序列 a，记当前遍历到的元素为 a[i]，我们把 a[i] 对应的桶的值自增 1，把 i−1 位置的前缀和加入到答案中算贡献。
2. 我们在循环的过程中，我们把原序列分成了两部分，后半部部分已经遍历过（已入桶），前半部分是待遍历的（未入桶），那么我们求到的 i−1 位置的前缀和就是「已入桶」的元素中比 a[i] 小的元素的总和，而这些元素在原序列中排在 a[i] 的后面，但它们本应该排在 a[i] 的前面，这样就形成了逆序对。
3. 桶是稀疏的。离散化一个序列的前提是我们只关心这个序列里面元素的相对大小，而不关心绝对大小（即只关心元素在序列中的排名）；
4. 我们可以对原序列排序后去重，对于每一个 a[i] 通过二分查找的方式计算排名作为离散化之后的值。当然这里也可以不去重，不影响排名。

时间复杂度：离散化的过程中使用了时间代价为 O(nlogn) 的排序，单次二分的时间代价为 O(logn)，一共有 n 次，总时间代价为 O(nlogn)；循环执行 n 次，每次进行 O(logn) 的修改和 O(logn) 的查找，总时间代价为 O(nlogn)。故渐进时间复杂度为 O(nlogn)。
空间复杂度：O(n)。

class Solution 
    public int reversePairs(int[] nums) 
        int n = nums.length;
        int[] tmp = new int[n];
        System.arraycopy(nums, 0, tmp, 0, n);
        // 离散化去重
        Arrays.sort(tmp);
        for (int i = 0; i < n; ++i) 
            nums[i] = Arrays.binarySearch(tmp, nums[i]) + 1;
        
        // 树状数组统计逆序对
        BIT bit = new BIT(n);
        int ans = 0;
        for (int i = n - 1; i >= 0; --i) 
            ans += bit.query(nums[i] - 1);
            bit.update(nums[i]);
        
        return ans;
    


class BIT 
    private int[] tree;
    private int n;

    public BIT(int n) 
        this.n = n;
        this.tree = new int[n + 1];
    

    public static int lowbit(int x) 
        return x & (-x);
    

    public int query(int x) 
        int ret = 0;
        while (x != 0) 
            ret += tree[x];
            x -= lowbit(x);
        
        return ret;
    

    public void update(int x) 
        while (x <= n) 
            ++tree[x];
            x += lowbit(x);