日历拼图C++解法
Posted Harris-H
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了日历拼图C++解法相关的知识,希望对你有一定的参考价值。
日历拼图C++解法
0.介绍
任何一个日期都可以用8块拼图拼起来。
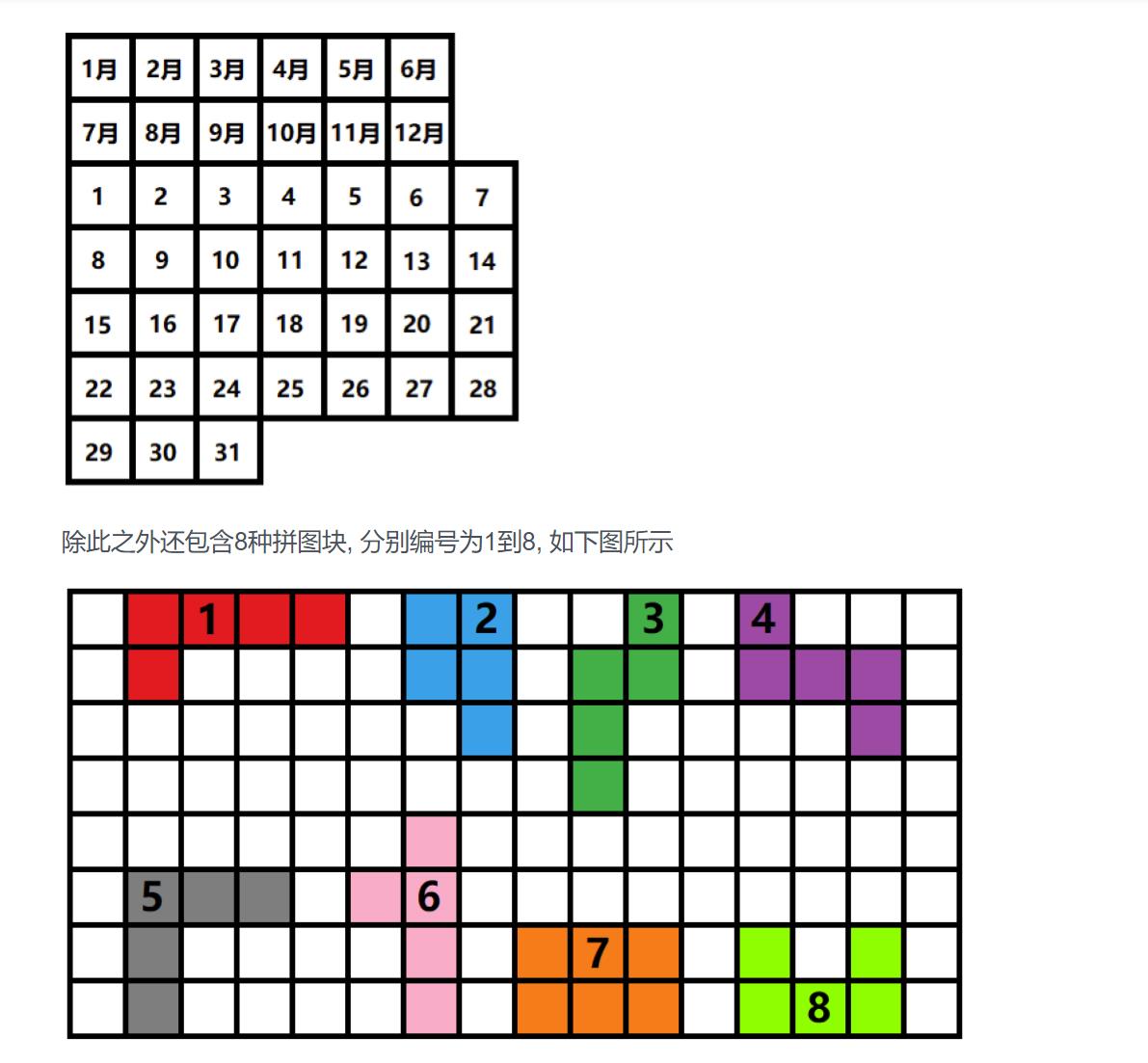
如12月3日:
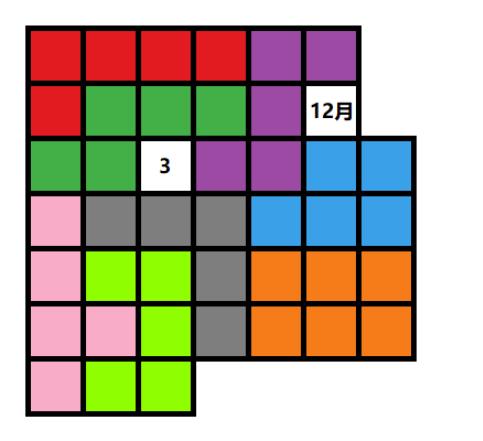
1.思路
主要的思想就是深度优先搜索。
a) 用字符串数组存8种拼图块
char a[9][5][5]=
'.','.','.','.',
'.','.','.','.',
'.','.','.','.',
'.','.','.','.',
'1','1','1','1',
'1','.','.','.',
'.','.','.','.',
'.','.','.','.',
'2','2','2','.',
'2','2','.','.',
'.','.','.','.',
'.','.','.','.',
'3','3','.','.',
'.','3','3','3',
'.','.','.','.',
'.','.','.','.',
'4','.','.','.',
'4','4','4','.',
'.','.','4','.',
'.','.','.','.',
'5','5','5','.',
'5','.','.','.',
'5','.','.','.',
'.','.','.','.',
'6','6','6','6',
'.','6','.','.',
'.','.','.','.',
'.','.','.','.',
'7','7','7','.',
'7','7','7','.',
'.','.','.','.',
'.','.','.','.',
'8','8','8','.',
'8','.','8','.',
'.','.','.','.',
'.','.','.','.';
b) 获得8种拼图块的8种放置方式
这里我使用旋转加翻转实现的。
[2] 最开始为第一个,然后翻转得到第二个。
[3] 再翻转回来,再顺时针90度得到第三个。
重复[2] [3] 步骤就可以得到8种放置方式。
翻转代码
也就是左右交换。
void filp(char a[5][5])
for(int i=0;i<4;i++)
for(int j=0;j<2;j++)
swap(a[i][j],a[i][3-j]);
旋转代码
这里我是顺时针旋转90度。
void rot(char a[5][5])
char b[5][5];
for(int i=0;i<4;i++)
for(int j=0;j<4;j++)
b[i][j] = a[3-j][i];
for(int i=0;i<4;i++)
for(int j=0;j<4;j++) a[i][j] = b[i][j];
c) 判断某一个位置是否可以放置对应的拼图块。
这里我们以左上角第一个非.的位置为起点,然后进行判断。
bool candown(int x,int y,int i,int j)
int sx = -1, sy = -1;
for(int xx=0;xx<4;xx++)
for(int yy=0;yy<4;yy++)
if(b[i][j][xx][yy] != '.')
sx = xx;
sy = yy;
int kx =sx,ky= sy;
while(kx<4 && ky<4)
int nx = x + kx-sx;
int ny = y + ky-sy;
//如果要覆盖
if(b[i][j][kx][ky]!='.')
if(nx<0 || ny<0) return false;
if(nx<2 && ny<=5)
if(mp[nx][ny]!='.') return false;
// mp[nx][ny] = b[i][j][kx][ky];
else if(nx<=5 && nx>=2 && ny<=6)
if(mp[nx][ny]!='.') return false;
// mp[nx][ny] = b[i][j][kx][ky];
else if(nx==6 && ny<=2)
if(mp[nx][ny]!='.') return false;
// mp[nx][ny] = b[i][j][kx][ky];
else return false;
if(ky==3)
kx++,ky=0;
else ky++;
return true;
return false;
d) 放置拼图块
与第c 步类似。
void down(int x,int y,int i,int j)
for(int xx=0;xx<4;xx++)
for(int yy=0;yy<4;yy++)
if(b[i][j][xx][yy] != '.')
int kx =xx,ky= yy;
while(kx<4 && ky<4)
int nx = x + kx-xx;
int ny = y + ky-yy;
if(b[i][j][kx][ky]!='.')
mp[nx][ny] = b[i][j][kx][ky];
if(ky==3)
kx++,ky=0;
else ky++;
return;
e) 回溯放置
与 d 步类似。
void undown(int x,int y,int i,int j)
for(int xx=0;xx<4;xx++)
for(int yy=0;yy<4;yy++)
if(b[i][j][xx][yy] != '.')
int kx =xx,ky= yy;
while(kx<4 && ky<4)
int nx = x + kx-xx;
int ny = y + ky-yy;
if(b[i][j][kx][ky]!='.')
mp[nx][ny] = '.';
if(ky==3)
kx++,ky=0;
else ky++;
return;
f) 深度优先搜索dfs
这里我用一维代替二维坐标,然后dfs的时候求出对应的位置。
然后就是简单带回溯的搜索了。
void dfs(int id)
int x = id/7;
int y = id%7;
if(x<2 && y==6)
dfs(id+1);
if(x==6 && y==3)
// printf("Success!\\n");
for(int i=0;i<7;i++)
for(int j=0;j<7;j++)
if(mp[i][j]=='.') continue;
putchar(mp[i][j]);
putchar('\\n');
exit(0);
if(mp[x][y]!='.') dfs(id+1);
for(int i=1;i<=8;i++)
if(!vis[i])
for(int j=1;j<=8;j++)
if(candown(x,y,i,j))
down(x,y,i,j);
vis[i] = 1;
dfs(id+1);
undown(x,y,i,j);
vis[i] = 0;
2.完整程序
我这里找到解就退出,如果想要找到每个解的所有情况,可以自行修改代码。即对应dfs里的exit(0) 去掉。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=1e3+5,M=2e8+5,inf=0x3f3f3f3f,mod=1e9+7;
const int hashmod[8] = 802653189,805306857,1610612781,998288353;
#define mst(a,b) memset(a,b,sizeof a)
#define db double
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define x first
#define y second
#define pb emplace_back
#define SZ(a) (int)a.size()
#define rep(i,a,b) for(int i=a;i<=b;++i)
#define per(i,a,b) for(int i=a;i>=b;--i)
#define ios ios::sync_with_stdio(false),cin.tie(nullptr)
void Print(int *a,int n)
for(int i=1;i<n;i++)
printf("%d ",a[i]);
printf("%d\\n",a[n]);
template <typename T> //x=max(x,y) x=min(x,y)
void cmx(T &x,T y)
if(x<y) x=y;
template <typename T>
void cmn(T &x,T y)
if(x>y) x=y;
char a[9][5][5]=
'.','.','.','.',
'.','.','.','.',
'.','.','.','.',
'.','.','.','.',
'1','1','1','1',
'1','.','.',