python 笔记 size-constrained-clustering （对类别大小做限制的聚类问题）

Posted 2022-02-22 UQI-LIUWJ

大小限制的聚类问题

1 主要方法

# 导入库
from size_constrained_clustering import fcm, equal, minmax, shrinkage,da
# by default it is euclidean distance, but can select others
from sklearn.metrics.pairwise import haversine_distances
from sklearn.datasets import make_blobs
import numpy as np
import matplotlib.pyplot as plt

1.1 Fuzzy C-means Algorithm

和KMeans类似，不过利用了归属概率（membership probability）进行计算，而不是直接的0或者1

n_samples = 2000
n_clusters = 4
centers = [(-5, -5), (0, 0), (5, 5), (7, 10)]
X, _ = make_blobs(n_samples=n_samples, n_features=2, cluster_std=1.0,
                    centers=centers, shuffle=False, random_state=42)
#生成数据集，每个主句两个特征值，一共2000个样本，四个分类，同时设定了聚类中心点的位置


model = fcm.FCM(n_clusters)

# use other distance function: e.g. haversine distance
# model = fcm.FCM(n_clusters, distance_func=haversine_distances)

model.fit(X)

centers = model.cluster_centers_
'''
array([[ 0.06913083,  0.07352352],
       [-5.01038079, -4.98275774],
       [ 6.99974221, 10.01169349],
       [ 4.98686053,  5.0026792 ]])
模型拟合之后，样本聚类的中心点
'''

labels = model.labels_
#模型拟合后，每个样本的类别

plt.figure(figsize=(10,10))

colors=['red','green','blue','yellow']

for i,color in enumerate(colors):
    color_tmp=np.where(labels==i)[0]
    plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)

plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')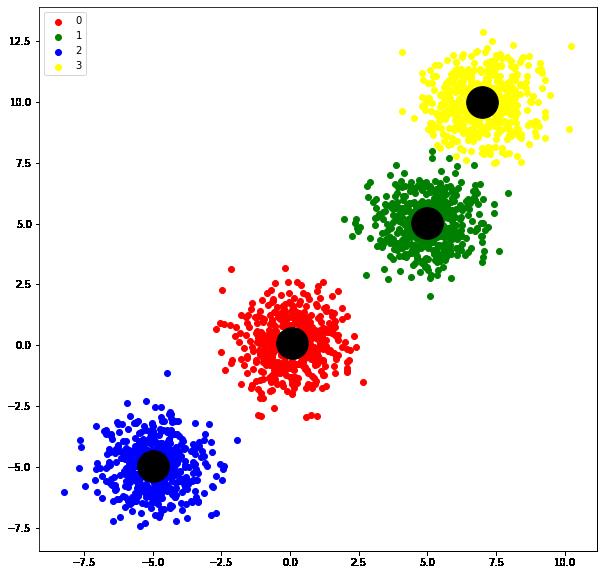

1. 2 Same Size Contrained KMeans Heuristics

利用启发式的方法获取等大聚类结果

n_samples = 2000
n_clusters = 4
X = np.random.rand(n_samples, 2)
# use minimum cost flow framework to solve
model = equal.SameSizeKMeansHeuristics(n_clusters)

model.fit(X)
centers = model.cluster_centers_
labels = model.labels_

import matplotlib.pyplot as plt
plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']
for i,color in enumerate(colors):
    color_tmp=np.where(labels==i)[0]
    plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)
plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')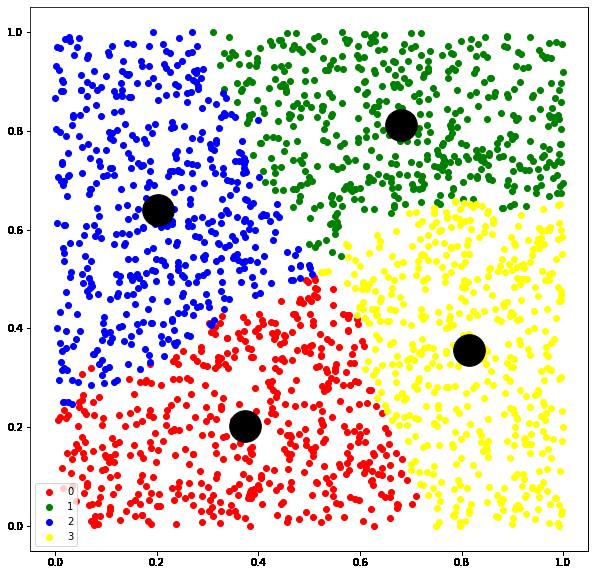

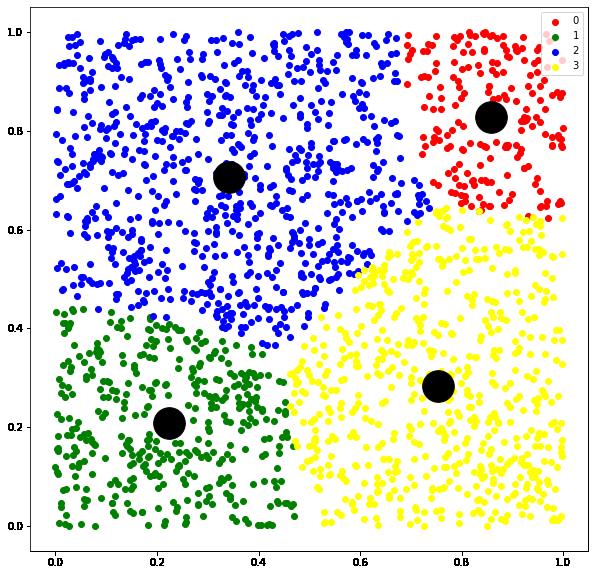
1.3 Same Size Contrained KMeans Inspired by Minimum Cost Flow Problem：

将聚类转换为分配问题，并用最小费用流的思路进行求解

n_samples = 2000
n_clusters = 4
X = np.random.rand(n_samples, 2)
# use minimum cost flow framework to solve
model = equal.SameSizeKMeansMinCostFlow(n_clusters)

model.fit(X)
centers = model.cluster_centers_
labels = model.labels_

plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']

for i,color in enumerate(colors):
    color_tmp=np.where(labels==i)[0]
    plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)

plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')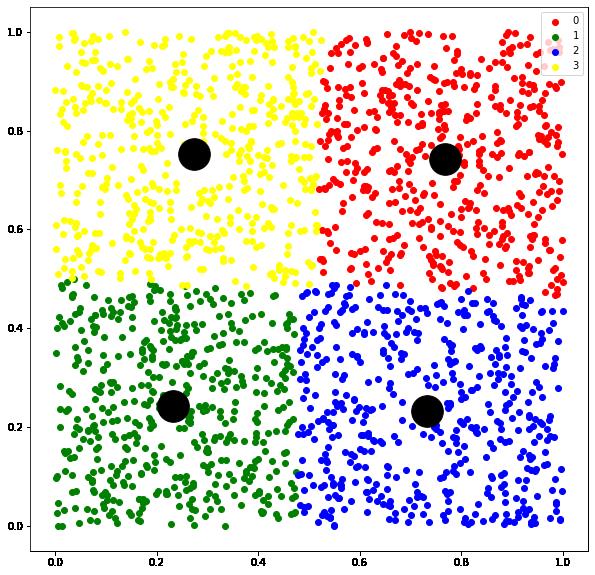

1.4 Minimum and Maximum Size Constrained KMeans Inspired by Minimum Cost Flow Problem

将聚类转换为分配问题，并用最小费用流的思路进行求解，加入最小和最大聚类规模限制

n_samples = 2000
n_clusters = 4
X = np.random.rand(n_samples, 2)
# use minimum cost flow framework to solve

model = minmax.MinMaxKMeansMinCostFlow(
    n_clusters, 
    size_min=200,   
    size_max=800)

model.fit(X)
centers = model.cluster_centers_
labels = model.labels_


plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']
for i,color in enumerate(colors):
    color_tmp=np.where(labels==i)[0]
    plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)
plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')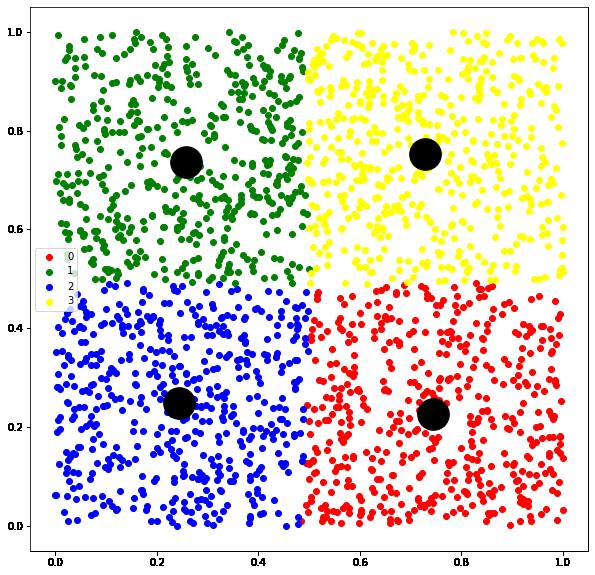

1.5 Deterministic Annealling Algorithm:

输入目标每类规模比例，获得相应聚类规模的结果。

n_samples = 2000
n_clusters = 4
X = np.random.rand(n_samples, 2)
# use minimum cost flow framework to solve
model =  da.DeterministicAnnealing(
    n_clusters, 
    distribution=[0.1, 0.2,0.4, 0.3])

model.fit(X)
centers = model.cluster_centers_
labels = model.labels_


plt.figure(figsize=(10,10))
colors=['red','green','blue','yellow']
for i,color in enumerate(colors):
    color_tmp=np.where(labels==i)[0]
    plt.scatter(X[color_tmp,0],X[color_tmp,1],c=color,label=i)
plt.legend()
plt.scatter(centers[:,0],centers[:,1],s=1000,c='black')