Python 自定义指标聚类

Posted 2022-02-20 荷碧·TZJ

最近在研究 Yolov2 论文的时候，发现作者在做先验框聚类使用的指标并非欧式距离，而是IOU。在找了很多资料之后，基本确定 Python 没有自定义指标聚类的函数，所以打算自己做一个

设训练集的 shape 是 [n_sample, n_feature]，基本思路是：

• 簇中心初始化：第 1 个簇中心取样本的特征均值，shape = [n_feature, ]；从第 2 个簇中心开始，用距离函数 (自定义) 计算每个样本到最近中心点的距离，归一化后作为选取下一个簇中心的概率 —— 迭代到选取到足够的簇中心为止
• 簇中心调整：训练多轮，每一轮以样本点到最近中心点的距离之和作为 loss，梯度下降法 + Adam 优化器逼近最优解，在 loss 浮动值小于阈值时停止训练

因为设计之初就打算使用自定义距离函数，所以求导是很大的难题。笔者不才，最终决定借助 PyTorch 自动求导的天然优势

先给出欧式距离的计算函数

def Eu_dist(data, center):
    """ 以 欧氏距离 为聚类准则的距离计算函数
        data: 形如 [n_sample, n_feature] 的 tensor
        center: 形如 [n_cluster, n_feature] 的 tensor"""
    data = data.unsqueeze(1)
    center = center.unsqueeze(0)
    dist = ((data - center) ** 2).sum(dim=2)
    return dist

然后就是聚类器的代码：使用时只需关注 __init__、fit、classify 函数

import torch
import numpy as np
Adam = torch.optim.Adam

class Cluster:
    """ 聚类器
        n_cluster: 簇中心数
        dist_fun: 距离计算函数
            kwargs:
                data: 形如 [n_sample, n_feather] 的 tensor
                center: 形如 [n_cluster, n_feature] 的 tensor
            return: 形如 [n_sample, n_cluster] 的 tensor
        init: 初始簇中心
        max_iter: 最大迭代轮数
        lr: 中心点坐标学习率
        stop_thresh: 停止训练的loss浮动阈值
        cluster_centers_: 聚类中心
        labels_: 聚类结果"""

    def __init__(self, n_cluster, dist_fun, init=None, max_iter=300, lr=0.08, stop_thresh=1e-4):
        self.n_cluster = n_cluster
        self.dist_fun = dist_fun
        self.max_iter = max_iter
        self.lr = lr
        self.stop_thresh = stop_thresh
        # 初始化参数
        self.cluster_centers_ = tensor(init) if init else None
        self.labels_ = None

    def fit(self, data):
        """ data: 形如 [n_sample, n_feature] 的 tensor
            return: loss浮动日志"""
        if self.cluster_centers_ is None:
            self._init_cluster(data, self.max_iter // 5)
        log = self._train(data, self.max_iter, self.lr)
        # 开始若干轮次的训练，得到loss浮动日志
        self.classify(data)
        # 对样本进行分类
        return log

    def classify(self, data):
        """ data: 形如 [n_sample, n_feature] 的 tensor
            return: 分类标签"""
        dist = self.dist_fun(data, self.cluster_centers_)
        self.labels_ = dist.argmin(axis=1)
        # 将标签加载到实例属性
        return self.labels_

    def _init_cluster(self, data, epochs):
        self.cluster_centers_ = data.mean(dim=0).reshape(1, -1)
        for _ in range(1, self.n_cluster):
            dist = np.array(self.dist_fun(data, self.cluster_centers_).min(dim=1)[0])
            new_cluster = data[np.random.choice(range(data.shape[0]), p=dist / dist.sum())].reshape(1, -1)
            # 取新的中心点
            self.cluster_centers_ = torch.cat([self.cluster_centers_, new_cluster], dim=0)
            self._train(data, epochs, self.lr * 2.5)
            # 初始化簇中心时使用较大的lr

    def _train(self, data, epochs, lr):
        center = self.cluster_centers_.cuda()
        center.requires_grad = True
        data = data.cuda()
        optimizer = Adam([center], lr=lr)
        # 将中心数据加载到 GPU 上
        update_log = []
        min_loss = np.inf
        for epoch in range(epochs):
            # 对样本分类并更新中心点
            dist = self.dist_fun(data, center)
            loss = dist.min(axis=1)[0].sum()
            # loss 函数: 所有样本到中心点的最小距离和
            loss.backward()
            optimizer.step()
            optimizer.zero_grad()
            # 反向传播梯度更新中心点
            loss = loss.item()
            progress = min_loss - loss
            update_log.append(progress)
            if progress > 0:
                self.cluster_centers_ = center.cpu().detach()
                min_loss = loss
                # 脱离计算图后记录中心点
                if progress < self.stop_thresh:
                    break
        return update_log

与KMeans++比较

KMeans++ 是以欧式距离为聚类准则的经典聚类算法。在 iris 数据集上，KMeans++ 远远快于我的聚类器。但在我反复对比测试的几轮里，我的聚类器精度也是不差的 —— 可以看到下图里的聚类结果完全一致

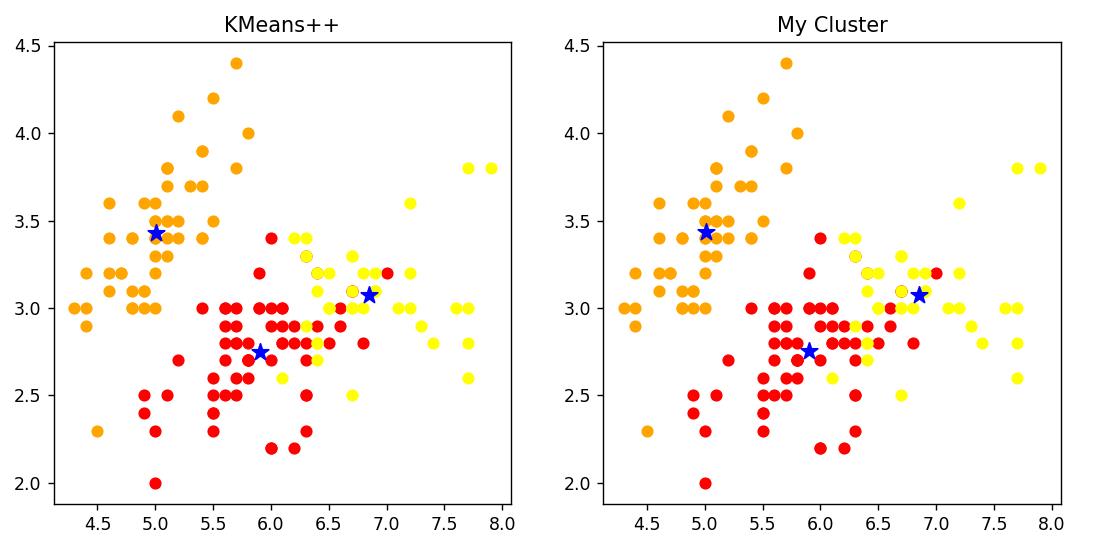
	KMeans++	My Cluster
Cost	145 ms	1597 ms
Center	[[5.9016, 2.7484, 4.3935, 1.4339], [5.0060, 3.4280, 1.4620, 0.2460], [6.8500, 3.0737, 5.7421, 2.0711]]	[[5.9016, 2.7485, 4.3934, 1.4338], [5.0063, 3.4284, 1.4617, 0.2463], [6.8500, 3.0741, 5.7420, 2.0714]]

虽然速度方面与老牌算法对比的确不行，但是我的这个聚类器最大的亮点还是自定义距离函数

Yolo 检测框聚类

在目标检测领域里，IOU 是指两个检测框的交并比 (交区域的面积 / 并区域的面积)。Yolov2 作者做检测框聚类的时候，以 1 - IOU 来计算两个检测框的距离。距离函数定义如下：

def neg_IOU_dist(data, center):
    """ 以 (1 - IOU) 为聚类准则的距离计算函数
        data: 形如 [n_sample, 2] 的 tensor
        center: 形如 [n_cluster, 2] 的 tensor"""
    n_sample = data.shape[0]
    n_cluster = center.shape[0]
    union_inter = (torch.prod(data, dim=1) + torch.prod(center, dim=1)).reshape(1, -1)
    data = data.unsqueeze(1).repeat(1, n_cluster, 1)
    center = center.unsqueeze(0).repeat(n_sample, 1, 1)
    inter = torch.prod(torch.stack([data, center], dim=2).min(dim=2)[0], dim=2)
    dist = 1 - inter / (union_inter - inter)
    return dist

Adam 优化器不像 SGD 一样容易陷入局部最优解，从我做神经网络的经验看，优化这种简单函数不成问题。但是验证就还没有时间做，可以的话后续会补上 COCO 数据集检测框的聚类结果