基于BP神经网络的分段函数连续优化问题
Posted hellobigorange
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了基于BP神经网络的分段函数连续优化问题相关的知识,希望对你有一定的参考价值。
·基于BP神经网络的分段函数连续优化问题
文章目录
摘要:
有些优化问题中的目标函数或者约束函数是分段函数,该类函数不具有连续性和可微性,也即不符合非线性规划问题求解的最优性条件,因而传统的梯度类算法难以求解此类优化问题。利用神经网络较强的非线性映射能力,结合最小二乘法可以进行曲线拟合的特点,提出一种将分段函数处理成具有连续而且可微性的函数的方法。最后进行实例验证,并进行误差分析,结果表明该方法处理得出的连续且可微的函数对分段函数的逼近精度较高,可以利用该函数进行优化求解。
一、问题描述
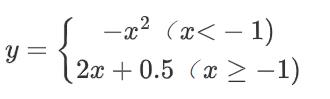
上式为一分段函数,其间断点为 x = - 1,纵轴分段距离为 0. 5,函数图像见图 5。要对其进行连续化处理,采用神经网络函数逼近方法得到一个精度比较高的连续函数去逼近。
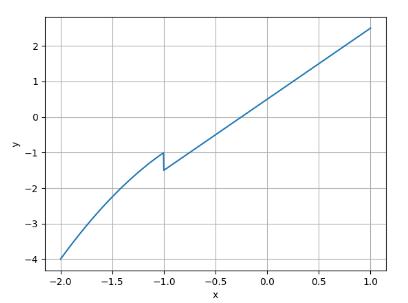
1、创建正态分布样本(断点处为 μ \\mu μ)
由于该分段函数分段点为 x = - 1,为了使得神经网络函数逼近得到的函数精度更高,逼近效果更好,所以取样本点要求在间断点 x = - 1 近的领域样本点密集,远的领域样本点稀疏,呈现正态分布。x为随机取出一组正态分布的数据,其中 μ 取-1,σ 取 0. 5,共取出 300 个数据。绘制样本点x的直方图和概率密度曲线。
经实验,若直接采用均匀分布采样,在分断点处的拟合效果不好。因此采用正态分布,让采样点在分断点处分布密集一些。
import numpy as np
import matplotlib.pyplot as plt
import random
import seaborn as sns
# 在断点处,产生一组满足正太分布的随机数
x = [random.normalvariate(-1, 0.5) for i in range(300)]
# x = np.linspace(-2.5,300)
x.sort()
# 绘制直方图和概率密度曲线
sns.distplot(x)
plt.show()
# 分段函数
y = list(map(lambda x: -x ** 2 if x < -1 else 2 * x + 0.5, x))
# 绘制正态分布后生成的样本点
plt.scatter(x, y, marker='x')
plt.grid(True)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
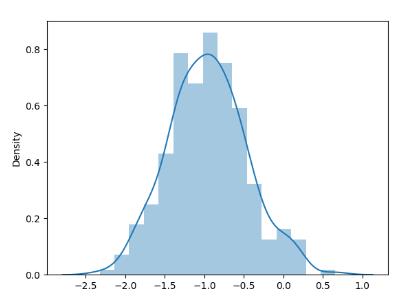
正态分布采样后的曲线
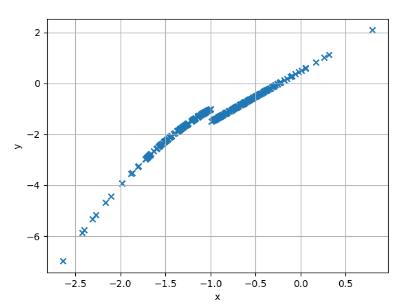
2、BP神经网络拟合分段函数并连续化
为了使建立的神经网络具有更好的性能,须对输入样本先进行归一化处理。采用MinMaxScaler()
网络结构如下:
激活函数:dense_1、dense_2都选择sigmoid,dense_3选择linear; batch_size = 100, epochs = 5000;optimizer = adam
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 20) 40
_________________________________________________________________
dense_2 (Dense) (None, 20) 420
_________________________________________________________________
dense_3 (Dense) (None, 1) 21
=================================================================
Total params: 481
Trainable params: 481
Non-trainable params: 0
_________________________________________________________________
# 归一化处理
from sklearn.preprocessing import MinMaxScaler
x=np.array(x).reshape(-1,1)
scaler = MinMaxScaler()
x=scaler.fit_transform(x)
#3 建立一个简单BP神经网络模型
from keras.optimizers import SGD,adam
from keras.optimizers import RMSprop
from keras.models import Sequential
from keras.layers.core import Dense, Activation
model = Sequential()
model.add(Dense(20, activation = 'sigmoid', input_shape = (1,)))
#model.add(Dropout(0.2))
model.add(Dense(20, activation = 'sigmoid'))
#model.add(Dropout(0.2))
model.add(Dense(1, activation = 'linear'))
model.summary()
model.compile(loss = 'mse', optimizer = adam(),)
model.fit(x, y, batch_size = 100, epochs = 5000, verbose =0 )
y_hap = model.predict(x)
error = np.mean((y-y_hap.reshape(1,300)[0])**2)
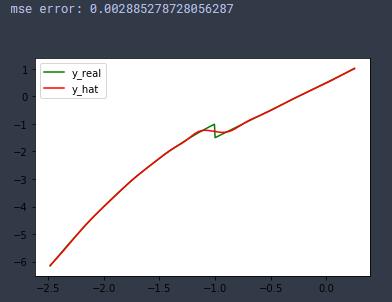
print('mse error:',error)
x1=scaler.inverse_transform(x)
plt.plot(x1,y,'g')
plt.plot(x1,y_hap,'r')
plt.legend(['y_real','y_hat'],loc = 'best')
plt.show()
# 神经网络前向传播得到连续函数方程
# print(model)
# layer1 = model.get_layer(index=1)
# weights = model.get_weights() #获取该层的参数W和b
# print(weights)
# w1,w2,w3=[-2.9336276, -9.499484 , 2.2418737]
# b1,b2,b3 = [ 2.1653745 , 0.55549806, -1.1913288 ]
# w4,w5,w6 = [-3.8131456,-4.3417945,2.4675584]
# b=0.21171658
# f = lambda x:1/(1+np.exp(-x))
# f_BP = lambda x:f(w1*x+b1)*w4+f(w2*x+b2)*w5+f(w3*x+b3)*w6+b
# x=x.reshape(1,300)[0]
# y_BP =[f_BP(x) for x in x]
# # print(y_BP)
# plt.plot(x1,y_BP,'g')
# plt.plot(x1,y_hap,'r')
# plt.legend(['y_REVERSE','y_original'],loc = 'best')
# plt.show()
3、最小二乘法拟合并得到方程
由于激活函数采用sigmoid和linear函数,经BP网络拟合后,若写出整个前向传播过程已经是一个连续函数了。但考虑神经网络有两层,总计481个参数,写出整个前向传播过程的函数不是一件容易的事情,因此考虑用最小二乘拟合BP网络拟合后的样本。得到一个多项式方程,方便后续优化处理。
使用最小二乘法进行拟合经过BP网络预测出的样本点,设置多项式次数为28次(实验获得)
x=x.reshape(1,300)[0]
x1=x1.reshape(1,300)[0]
y_hap=y_hap.reshape(1,300)[0]
# 最小二乘法拟合
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
# 多项式
def fit_func(p, x):
f = np.poly1d(p)
return f(x)
# 残差
def residuals_func(p, x, y):
ret = fit_func(p, x) - y
return ret
M=28 # 多项式的次数
p_init= p_init = np.random.rand(M + 1)
p_lsq = leastsq(residuals_func, p_init, args=(x1, y)) # 拟合得到最终的多项式参数
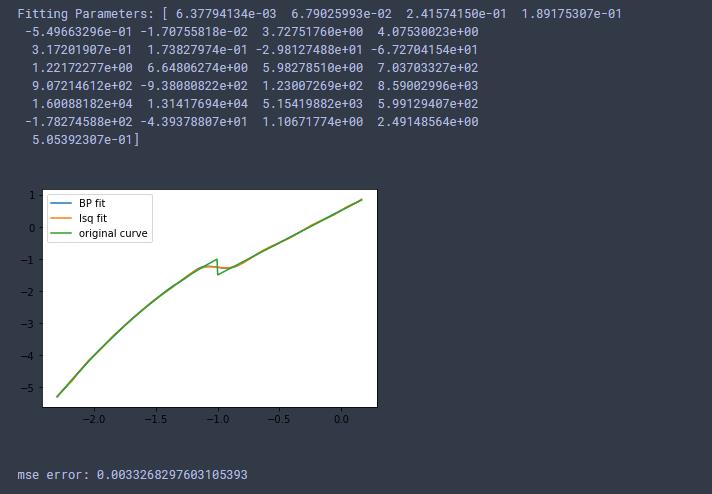
print('Fitting Parameters:', p_lsq[0])
y_lsq=fit_func(p_lsq[0], x1)
# 可视化
plt.plot(x1, y_hap, label='BP fit')
plt.plot(x1, y_lsq, label='lsq fit')
plt.plot(x1,y, label='original curve')
plt.legend()
plt.show()
error = np.mean((y-y_lsq.reshape(1,300)[0])**2)
print('mse error:',error)
4、结论:
本文使用了 BP 神经网络对分段函数进行连续化处理,样本输入点集为自变量区间的离散点组成的集合,并且考虑了分段函数间断点对函数值间距的影响,所取出的样本点集满足正态分布特性,从而对间断点附件的函数值预测效果更佳。最后结合最小二乘法曲线拟合的方法得出了具体的函数表达式,有助于该类优化问题的进一步优化求解。
5、思考
1、为什么不使用最小二乘拟合分段函数?
经试验,直接用最小二乘法拟合分段函数,结果如下:
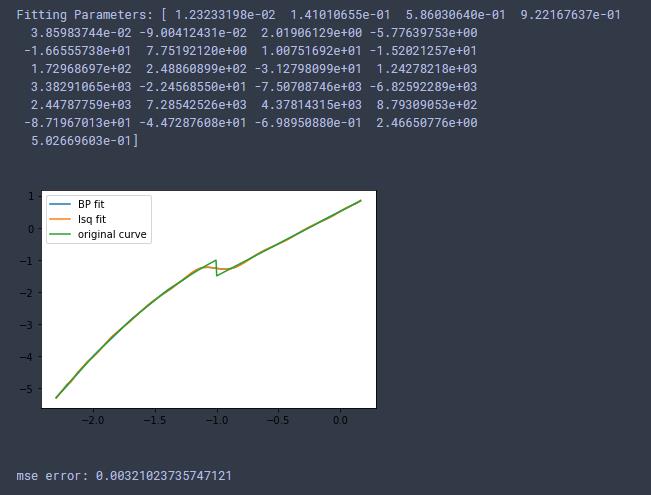
这表明直接用最小二乘拟合分段函数效果可能更好(但最小二乘拟合效果,确实没有直接用BP网络拟合的要好)。因此论文可取之处可能是分断点处正态分布采样。
2、为什么要将分段函数连续化
为什要经过将分段函数变为连续函数的过程,是为了避免梯度震荡吗?文章提出是为了使用梯度法 求解最优化问题,但现在次梯度法和Adam都可以直接求解分段函数的最优化问题。
(留到看完梯度法解决最优化问题后再思考)
注:本文参考自《基于 BP 神经网络的分段函数连续优化处理》冯长敏,张炳江
以上是关于基于BP神经网络的分段函数连续优化问题的主要内容,如果未能解决你的问题,请参考以下文章