leetcode之并查集刷题总结1
Posted nuist__NJUPT
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了leetcode之并查集刷题总结1相关的知识,希望对你有一定的参考价值。
leetcode之并查集刷题总结1
1-省份数量
题目链接:题目链接戳这里!!!
思路:每次判断当前边为1时,两个顶点是否式一个集合,也就是通过find函数判断是否是同一个爹,不是则不连通,则ans减少1,同时把将当前两个顶点合并为一个集合。
class Solution
public int findCircleNum(int[][] isConnected)
int n = isConnected.length ;
int [] parent = new int [n] ;
for(int i=0; i<n; i++)
parent[i] = i ;
int ans = n ;
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
if(i!=j && isConnected[i][j]==1)
int root1 = find(i, parent) ;
int root2 = find(j, parent) ;
if(root1 != root2)
parent[root1] = root2 ;
ans --;
return ans ;
public int find(int x, int [] parent) //找爹方法
if(x != parent[x])
parent[x] = find(parent[x], parent) ;
return parent[x] ;
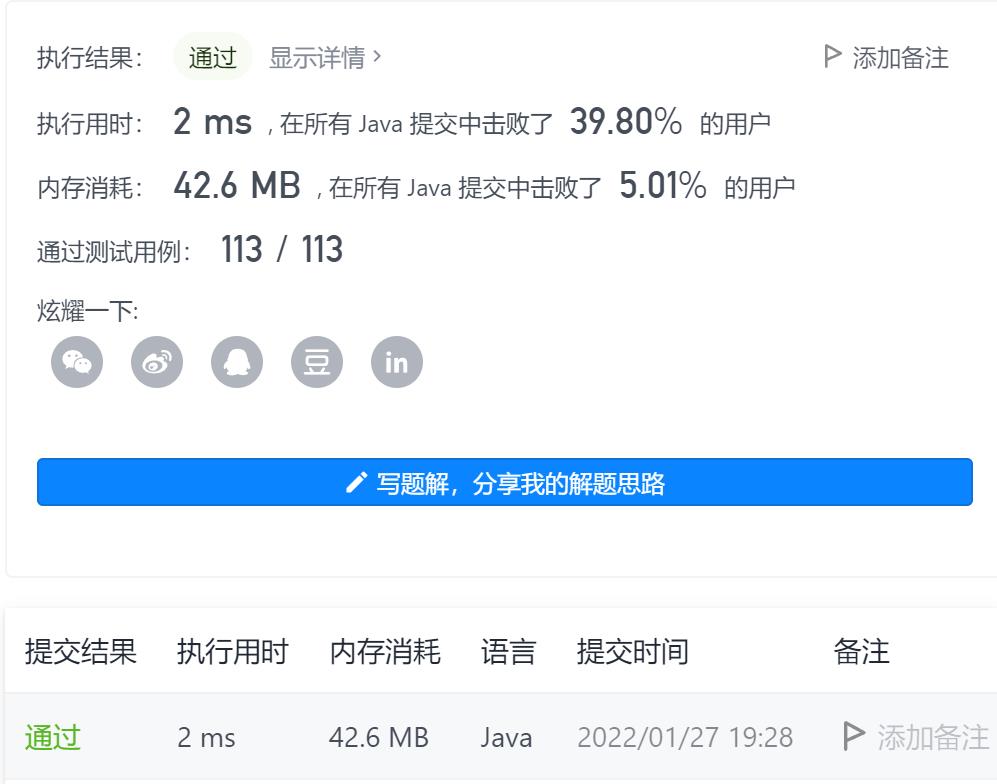
2-最长连续序列
题目链接:题目链接戳这里!!!
思路:这个是直接用的set集合排序去重,然后遍历比较最长连续。
class Solution
public int longestConsecutive(int[] nums)
Set<Integer> set = new TreeSet<>() ;
for(int i=0; i<nums.length; i++)
set.add(nums[i]) ; //排序去重
List<Integer> list = new ArrayList<>(set) ;
if(list.size()==1)
return 1 ;
int cnt = 1, max = 0 ;
for(int i=0; i<set.size()-1; i++)
if(list.get(i)+1==list.get(i+1)) //累加相邻的
cnt ++;
else
cnt = 1;
if(cnt > max)
max = cnt ; //找出最大相邻
return max ;

思路2:并查集,将所有连续的数放到一个集合,找到当前节点与集合根节点的之差的最大值,就是最长连续序列的长度。
不过说实话,还没有直接set去重排序,暴力对比的效率高。
class Solution
Map<Integer,Integer> parent = new HashMap<>() ;
public int longestConsecutive(int[] nums)
//并查集,将所有连续的放到一个集合,找出当前节点减根节点的最大值
int max = 0 ;
init(nums) ; //初始化。也相当于去重了
for(int val : nums) //将所有的连续的数字放到一个集合
union(val, val+1) ;
for(int val : nums) //当前节点减取根节点的最大值
max = Math.max(max, val-find(val)+1) ;
return max ;
public void init(int [] nums) //初始化方法
for(int i=0; i<nums.length; i++)
parent.put(nums[i],nums[i]) ;
public void union(int x, int y) //合并方法
Integer root1 = find(x) ;
Integer root2 = find(y) ;
if(root1==root2)
return ;
if(root1==null || root2==null)
return ;
parent.put(root2, root1);
private Integer find(int a) //找根方法
if (!parent.containsKey(a)) return null;
while (parent.get(a) != a)
parent.put(a, parent.get(parent.get(a)));
a = parent.get(a);
return a;
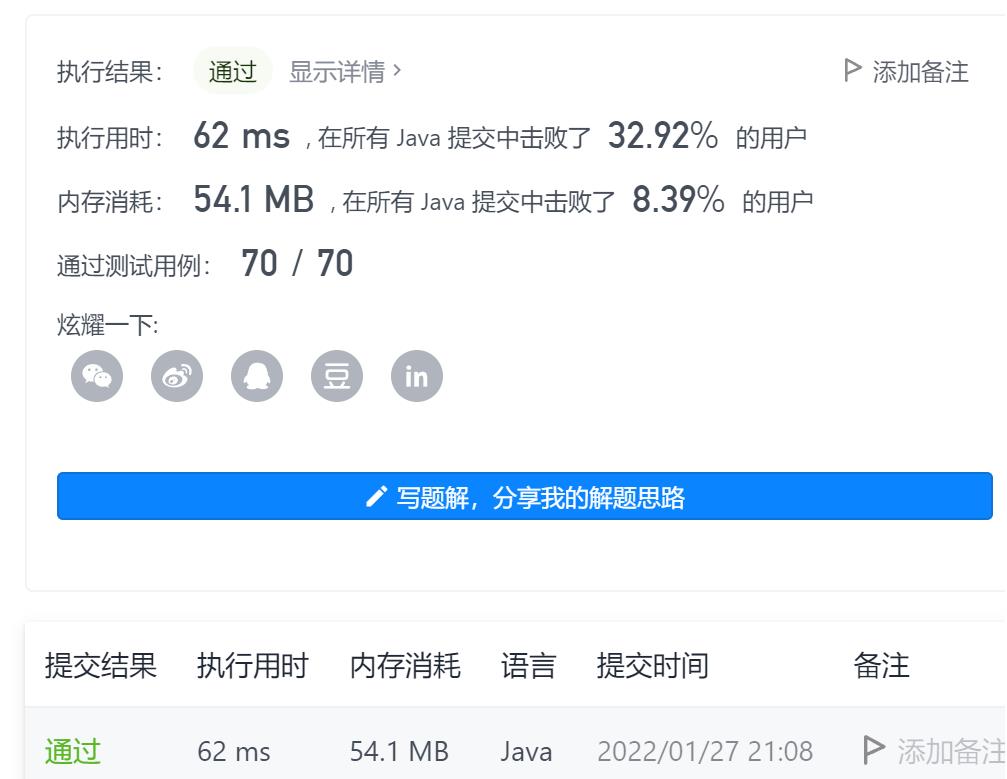
3-冗余连接
题目链接:题目链接戳这里!!!
思路:就是用并查集将所有不在一个集合的两个端点放到一个集合,最后形成环的那条边的两个端点就是我们要删除的边,留下来的就是树。
AC代码入下:
class Solution
int [] parent ;
int [] res ;
public int[] findRedundantConnection(int[][] edges)
//用并查集划分集合,已经在一个集合的就不需要放到一起
int n = edges.length ;
res = new int [2] ;
parent = new int [n+1] ;
init(n) ;
for(int i=0; i<edges.length; i++)
union(edges[i][0], edges[i][1], res) ;
return res ;
public void init(int n)
for(int i=1; i<=n; i++)
parent[i] = i ;
public int find(int x)
if(x != parent[x])
return parent[x] = find(parent[x]) ;
return parent[x] ;
public void union(int x, int y, int [] res)
int root1 = find(x) ;
int root2 = find(y) ;
if(root2==root1)
res[0] = x;
res[1] = y ;
return ;
parent[root2] = root1 ;
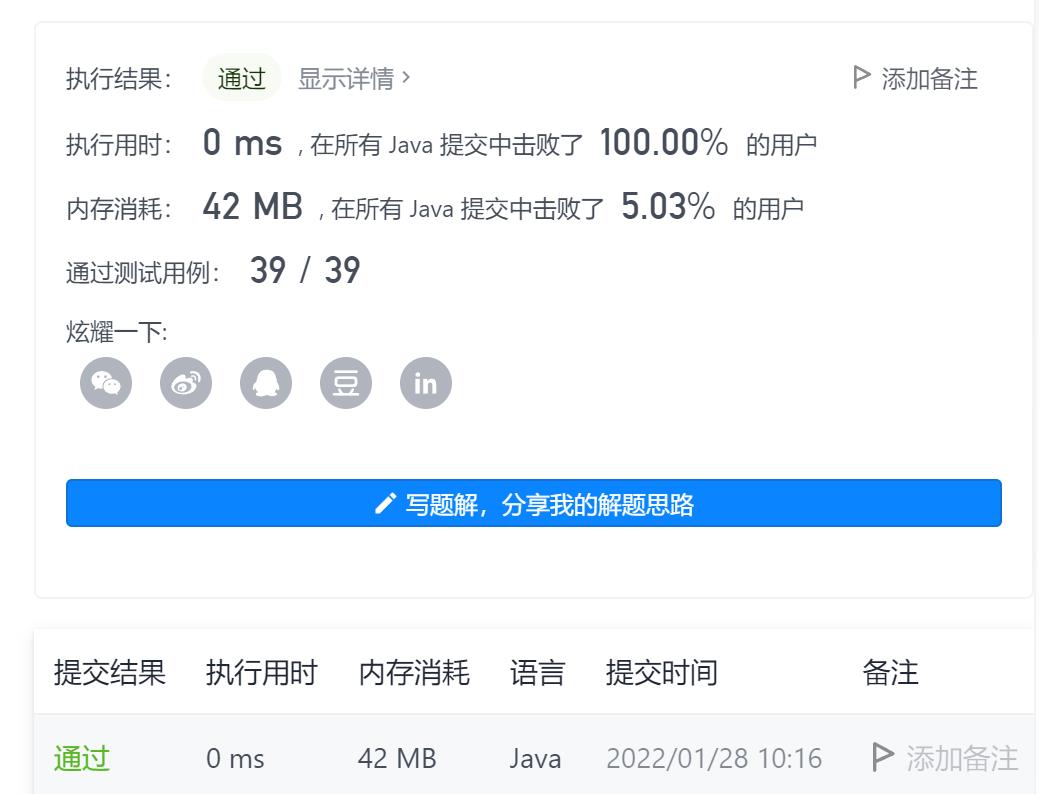
4-冗余连接II
题目链接:题目链接戳这里!!!
思路:这题相比上一题要难一些,这一题换成了有向图,直接考虑有没有环行不通的。
首先记录每个顶点的入度。
因为是删除最后一个,需要从后向前遍历。
对入度为2的边,删除该边后,若剩余边连在一起不形成环,则该边就是我们要删除的边。
对于入度为1的边,删除该边后,若剩余的边连在一起不形成环,则该边就是我们要删除的边。
AC代码入下:
class Solution
int [] parent ;
int [] res ;
int [] degrees ; //节点的入度
public int[] findRedundantDirectedConnection(int[][] edges)
int n = edges.length ;
parent = new int [n+1] ;
degrees = new int [n+1] ;
res = new int [2] ;
for(int i=0; i<n; i++) //初始化入度
degrees[edges[i][1]] ++ ;
init(n) ;
for(int i=n-1; i>=0; i--)
if(degrees[edges[i][1]] == 2)
if(judge(edges, n, i)) //删除入度为2的边不构成环
return edges[i] ;
for(int i=n-1; i>=0; i--)
if(degrees[edges[i][1]] == 1) //删除入度为1的边不构成环
if(judge(edges, n, i))
return edges[i] ;
return edges[1] ; //这个返回随意,因为不会走到这一步的
public boolean judge(int [][]edges, int len, int index)
for(int i=0; i<len; i++)
if(index==i)
continue ; //当前这条边不要
if(!union(edges[i][0], edges[i][1]))
init(len) ; //还原parent数组,特别重要,别忘了
return false ; //构成环
return true ;
public void init(int n)
for(int i=1; i<=n;i++)
parent[i] = i ;
public int find(int x)
if(x != parent[x])
return parent[x] = find(parent[x]) ;
return parent[x] ;
public boolean union(int x, int y)
int root1 = find(x) ;
int root2 = find(y) ;
if(root1 == root2) //有环,不能合并
return false;
parent[root1] = root2 ;
return true ; //没环,可以合并

5-岛屿的最大面积
题目链接:题目链接戳这里!!!
思路:这题用的深搜,每个点等于1,则沿着四个方向搜索并标记为0,同时记录修改的次数,比较所有连通块的修改次数,去最大值即可。
AC代码如下:
class Solution
int max = 0, res = 0 ;
int [] offsetX = -1,1,0,0 ;
int [] offsetY = 0,0,-1,1 ;
public int maxAreaOfIsland(int[][] grid)
int m = grid.length ;
int n = grid[0].length ;
for(int i=0; i<m; i++)
for(int j=0; j<n; j++)
if(grid[i][j]==1)
dfs(grid, i, j) ;
if(max > res)
res = max ;
max = 0 ;
return res ;
public void dfs(int [][]grid, int x, int y)
grid[x][y] = 0 ;
max ++ ;
for(int i=0; i<4; i++)
int nx = x + offsetX[i] ;
int ny = y + offsetY[i] ;
if(nx<0 || ny<0 || nx>grid.length-1 || ny>grid[0].length-1)
continue ;
if(grid[nx][ny] == 1)
dfs(grid, nx, ny) ;

6-飞地的数量
题目链接:题目链接戳这里!!!
思路:这题用的也是深搜,沿着四个方向搜索,能到边界就不累加,到不了边界的联通块的数量要累加起来。
class Solution
boolean flag = false ;
int cnt = 0, sum = 0 ;
int [] offsetX = -1,1,0,0 ;
int [] offsetY = 0,0,-1,1 ;
public int numEnclaves(int[][] grid)
int m = grid.length ;
int n = grid[0].length ;
for(int i=0; i<m; i++)
for(int j=0; j<n; j++)
if(grid[i][j] == 1)
dfs(grid, i, j) ;
if(flag)
cnt = 0 ;
flag = false ;
else
sum += cnt ;
cnt = 0 ;
return sum ;
public void dfs(int [][]grid, int x, int y)
if(x == 0 || y==0 以上是关于leetcode之并查集刷题总结1的主要内容,如果未能解决你的问题,请参考以下文章