向量的点乘与叉乘概念理解以及C++代码实现
Posted 非晚非晚
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了向量的点乘与叉乘概念理解以及C++代码实现相关的知识,希望对你有一定的参考价值。
文章目录
点乘与叉乘是线性代数的基本知识,在工作中也经常能够遇到,下面我们来温习一下它们的概念以及使用C++代码对它们进行实现。
1. 点乘
- 概念
向量的点乘,也叫点积、内积、数量积。是指在实数R上的两个向量的一种二元运算,这种运算返回一个实数值标量。点乘有两种定义方式:代数方式和几何方式。
- 代数方式
已知两个向量
a
→
=
[
a
1
,
a
2
,
.
.
.
,
a
n
]
\\overrightarrowa = [a_1, a_2,...,a_n]
a=[a1,a2,...,an]和
b
→
=
[
b
1
,
b
2
,
.
.
.
,
b
n
]
\\overrightarrowb = [b_1, b_2,...,b_n]
b=[b1,b2,...,bn],则向量
a
→
\\overrightarrowa
a与向量
b
→
\\overrightarrowb
b的内积代数定义为:
a
⋅
b
=
a
1
b
1
+
a
2
b
2
+
.
.
.
+
a
n
b
n
a\\cdot b=a_1b_1+a_2b_2+...+a_nb_n
a⋅b=a1b1+a2b2+...+anbn
代数表示:对应元素相乘相加。
- 几何定义(2维和3维)
已知两个向量
a
→
=
[
x
1
,
y
1
,
z
1
]
\\overrightarrowa = [x_1,y_1,z_1]
a=[x1,y1,z1]和
b
→
=
[
x
2
,
y
2
,
z
2
]
\\overrightarrowb=[x_2,y_2,z_2]
b=[x2,y2,z2],它们的模值分别为
∣
a
∣
|a|
∣a∣和
∣
b
∣
|b|
∣b∣,它们的夹角为
θ
∈
[
0
,
π
]
\\theta \\in \\ [0,\\pi]
θ∈ [0,π],那么向量
a
→
\\overrightarrowa
a与向量
b
→
\\overrightarrowb
b的几何定义为:
a
⋅
b
=
∣
a
∣
∣
b
∣
c
o
s
θ
a\\cdot b = |a||b|cos\\theta
a⋅b=∣a∣∣b∣cosθ
几何意义: 可以用来表示一个向量在另一个向量上的投影长度,为一个标量。
2. 叉乘
向量的叉乘,也叫叉积、外积、向量积,是一种在向量空间中(也就是说向量元素个数为3)向量的二元运算。与点积不同,叉乘的运算结果是一个向量而不是一个标量,并且两个向量的叉积与这两个向量所构成的平面垂直。
- 定义方式
已知两个向量 a → = [ x 1 , y 1 , z 1 ] \\overrightarrowa = [x_1,y_1,z_1] a=[x1,y1,z1]和 b → = [ x 2 , y 2 , z 2 ] \\overrightarrowb=[x_2,y_2,z_2] b=[x2,y2,z2],它们的模值分别为 ∣ a ∣ |a| ∣a∣和 ∣ b ∣ |b| ∣b∣,它们的夹角为 θ ∈ [ 0 , π ] \\theta \\in \\ [0,\\pi] θ∈ [0,π],那么向量 a → \\overrightarrowa a与向量 b → \\overrightarrowb b的叉乘表示为:
- 模值: ∣ a × b ∣ = ∣ a ∣ ∣ b ∣ s i n θ |a × b | = ∣ a ∣ ∣ b ∣ s i n θ ∣a×b∣=∣a∣∣b∣sinθ
- 方向:两个向量的叉积与这两个向量所构成的平面垂直,且遵循
右手准则(右手的四指从a以不超过180°的转角转向b时,竖起的大拇指指向是叉乘的方向。)
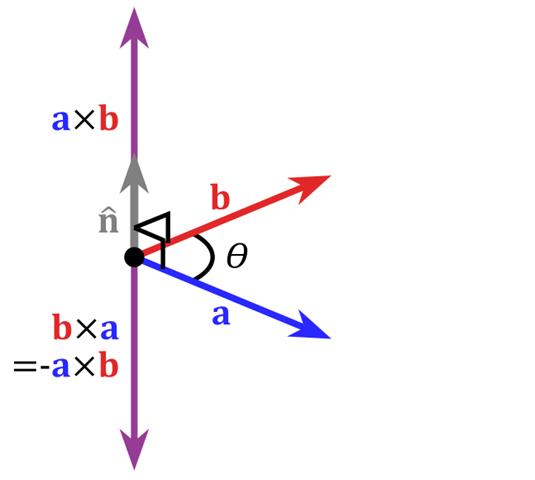
- 坐标运算
假设: i 、 j 、 k i、j、k i、j、k分别为XYZ三个轴的单位向量,则叉乘运算表示如下:
a → × b → = ∣ i j k x 1 y 1 z 1 x 2 y 2 z 2 ∣ = [ y 1 z 2 − y 2 z 1 , − ( x 1 z 2 − x 2 z 1 ) , x 1 y 2 − x 2 y 1 ] \\overrightarrowa×\\overrightarrowb = \\beginvmatrix i& j& k\\\\ x_1& y_1& z_1 \\\\ x_2& y_2& z_2 \\\\ \\endvmatrix=[y_1z_2-y_2z_1,-(x_1z_2-x_2z_1),x_1y_2-x_2y_1] a×b=∣∣∣∣∣∣ix1x2jy1y2kz1z2