AC算法在文本匹配中的应用

Posted 2022-02-03 行者AI

本文首发于：行者AI

在工作中需要对一些违禁词进行拦截，实际应用场景中，需保证匹配过程在数百毫秒内给出结果。因此，如何快速，准确的识别文本中是否包含了这些关键词就变得尤为重要。

对于上述问题我们描述为以下形式：

给定关键词集合P=p1,p2,……,pk，在目标串T[1…m]中找到出现了哪些关键词。

最容易想到的方法就是针对每个单词去匹配一遍，最后总结出都哪些单词匹配成功。

考虑KMP算法，单个关键词匹配的时间复杂度是O(|pk|+m)，所以，所有关键词都匹配一遍的时间复杂度为O(|p1|+m+|p2|+m+…+|pk|+m)。令n=|p1|+…+|pk|，上式化简为O(n+km)，因此，当关键词的数量变得非常多时，这种算法就变得无法忍受了。

Alfred V.Aho和Margaret J.Corasick在1974年提出了一个经典的多模式匹配算法-AC算法，这个算法可以保证对于给定的长度为n的文本，和模式集合Pp1,p2,…pm，在O(n)的时间复杂度内找到文本中的所有目标模式，而与模式集合的规模m无关。

1. AC算法详解

AC自动机的基础是Trie树, 和Trie树不同的是，树中的每个结点除了有指向孩子的指针，根据被查找的目标字段开始往叶子节点逐字符匹配。在这个过程中，如果发生失配，要根据失配跳转点进行跳转，如果找到匹配的模式串则进行打印输出。AC算法在扫描文本时完全不需要回溯，如果只考虑匹配的过程，该算法的时间复杂度为O(n)，也就是只跟待匹配文本的长度相关。

1.1 自动机

首先，我们解释下什么是AC自动机？ 什么是自动机？

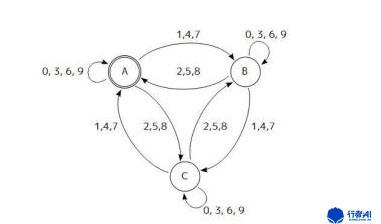
图1. 自动机状态转换图

自动机是有限状态机的数学模型，状态是什么？ 比如：开关有两种状态，筛子有6种状态，如图中所示有A、B、C三种状态。自动机就是在某些外界刺激下，能够改变状态的机器。图中A状态，通过0，3，6，9的刺激，能够回滚到本身状态，通过1，4，7刺激可以到达B状态。

AC将字符匹配转换为了状态转移。即AC通过构建自动机，将字串匹配的过程，转换为了在状态机之间状态的跳转来表示字符匹配过程。

1.2 具体实现

AC算法的实现可由以下三个部分构成：

• goto表：由模式集合中的所有模式构成的状态转移自动机
• failure表：在goto表中匹配失败后状态跳转的依据
• output表：表示输出，又称：emits，即代表到达某个状态后某个模式串匹配成功

（1）构造goto表

这里我们以集合P=“he”,”she”,”his”,”hers” 为例

首先是构建转向函数(goto)，指的是一种状态之间的转向关系，为了构建goto函数，我们需要建立一个状态转移图。开始，这个图只包含一个状态0，然后通过添加一条从起始状态出发的路径的方式，依次向图中输入每个关键字keyword，新的顶点和边被加入到图表中，这样就产生了一条能拼写出关键字keyword的路径。

添加第一个关键词“he”得到下图，其中从状态0到状态2的路径就拼写出了关键字“he”。

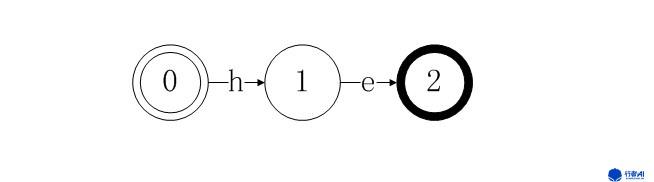
图2. he状态转移图

接着我们构建第二个关键词 “she”。

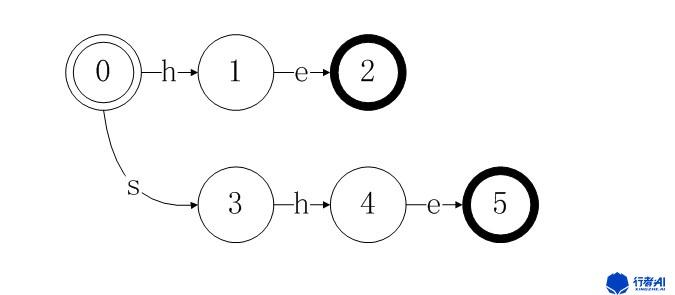
图3. she状态转移图

当我们增加“his”时，因为已经存在一条从状态0在输入h的条件下到达状态1的边，因此我们这里不需要另外添加一条同样的边。

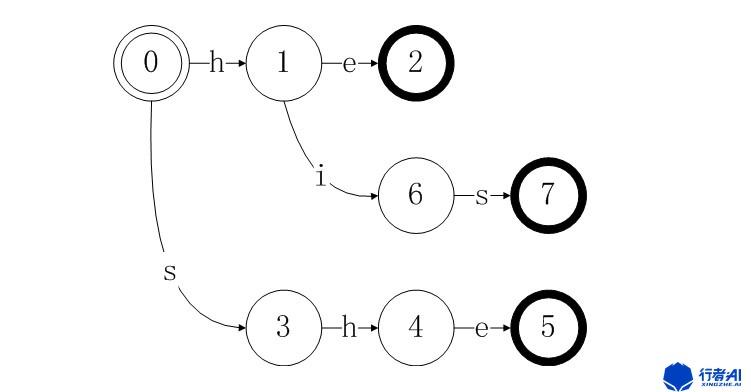
图4. his状态转移图

最后我们添加 “hers”，得到如下的链路，输出“hers”和状态9相关联，最后对除了h和s外的每个字符都增加一个从状态0到0的循环。

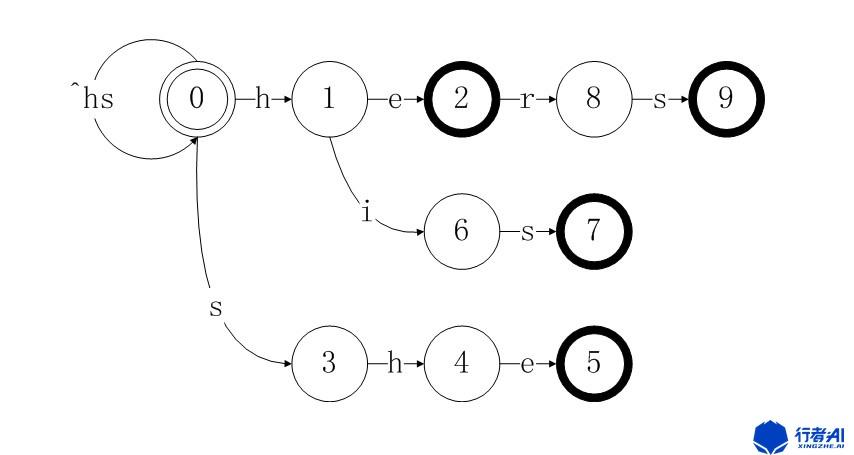
图5. hers状态转移图

至此，我们就构造了整个模式集合的状态转移图，也就是goto函数。

（2）构造failure表

失效函数failure决定了当goto函数得到的下一个状态无效时，应该回退到哪一个状态。

在构造fail函数时，我们首先要引入深度的概念，状态s的深度depth(s)定义为在goto表中从起始状态0到状态s的最短路径长度。如goto表中状态1和3的深度为1。

计算思路

先计算所有深度是1的状态的失效函数值，然后计算所有深度为2的状态，以此类推，直到所有状态（除了状态0，因为它的失效函数没有定义）的失效函数值都被计算出。

计算方法

用于计算某个状态失效函数值的算法在概念上是非常简单的。首先，令所有深度为1的状态s的函数值为f(s) = 0。假设所有深度小于d的状态的f值都已经被算出了，那么深度为d的状态的失效函数值将根据深度小于d的状态的失效函数值来计算。

计算过程

• 对于所有的字符a，如果goto(r,a) = fail，那么什么也不做（当r为我们上面构造的trie树的叶子节点时，就符合这种情况）
• 如果goto(r,a) == s，我们记state = fail®，执行state = f(state)零次或者若干次，直到使得goto(state,a) != fail，因为goto(0,a) != fail，所以这个状态是一定存在的
• 记fail(s) = goto(state,a)

以我们上面构造的状态图为例, 我们构造出的failure表如下：

状态	0	1	2	3	4	5	6	7	8	9
fail值	None	0	0	0	1	2	0	3	0	3

（3）构造output表

output表示输出，即代表到达某个状态后某个模式串匹配成功。该表的构造过程融合在goto表和failure表的构造过程中。

• 在构造goto表时，每个模式串结束的状态都加入到output表中，也就是goto表中的黑色加粗圆圈。得到：

  i	output(i)
  2	he
  5	she
  7	his
  9	hers

• 在构造failure表时，若f(s) = s’，则将s和s‘对应的output集合求并集。如f(5) = 2，则得到最终的output表为：

  i	output(i)
  2	he
  5	she, he
  7	his
  9	hers

2. AC算法具体实现

以python为例

class ac_automation(object):

    def __init__(self):
        self.root = node()

    def add(self, word):
        temp_root = self.root
        for char in word:
            if char not in temp_root.next:
                temp_root.next[char] = node()
            temp_root = temp_root.next[char]
        temp_root.isWord = True
        temp_root.word = word

    def make_fail(self):
        temp_que = []
        temp_que.append(self.root)
        while len(temp_que) != 0:
            temp = temp_que.pop(0)
            p = None
            for key,value in temp.next.item():
                if temp == self.root:
                    temp.next[key].fail = self.root
                else:
                    p = temp.fail
                    while p is not None:
                        if key in p.next:
                            temp.next[key].fail = p.fail
                            break
                        p = p.fail
                    if p is None:
                        temp.next[key].fail = self.root
                temp_que.append(temp.next[key])

    def search(self, content):
        p = self.root
        result = []
        currentposition = 0

        while currentposition < len(content):
            word = content[currentposition]
            while word in p.next == False and p != self.root:
                p = p.fail

            if word in p.next:
                p = p.next[word]
            else:
                p = self.root

            if p.isWord:
                result.append(p.word)

            currentposition += 1
        return result

---

PS：更多技术干货，快关注【公众号 | xingzhe_ai】，与行者一起讨论吧！