OpenGL教程 学习笔记
Posted 尚墨1111
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了OpenGL教程 学习笔记相关的知识,希望对你有一定的参考价值。
GLSL 语法https://blog.csdn.net/xhm01291212/article/details/79270836
python目录结构 https://www.cnblogs.com/xiao-apple36/p/8884398.html
OpenGL教程
1 概念
1.1 是什么?
一般它被认为是一个API,包含了一系列可以操作图形、图像的函数。然而,OpenGL本身并不是一个API,它仅仅是一个规范。OpenGL规范严格规定了每个函数该如何执行,以及它们的输出值。
1.2 核心模式与固定渲染管线模式
早期的OpenGL使用立即渲染模式(Immediate mode,也就是固定渲染管线),这个模式下绘制图形很方便。OpenGL的大多数功能都被库隐藏起来,开发者很少有控制OpenGL如何进行计算的自由。
而开发者迫切希望能有更多的灵活性,固定渲染管线效率太低。因此从OpenGL3.2开始,规范文档开始废弃立即渲染模式,并鼓励开发者在OpenGL的核心模式(Core-profile)下进行开发,这个分支的规范完全移除了旧的特性。
1.3 状态机
OpenGL自身是一个巨大的状态机(State Machine):一系列的变量描述OpenGL此刻应当如何运行。OpenGL的状态通常被称为OpenGL上下文(Context)。我们通常使用如下途径去更改OpenGL状态:设置选项,操作缓冲。最后,我们使用当前OpenGL上下文来渲染。
假设当我们想告诉OpenGL去画线段而不是三角形的时候,我们通过改变一些上下文变量来改变OpenGL状态,从而告诉OpenGL如何去绘图。一旦我们改变了OpenGL的状态为绘制线段,下一个绘制命令就会画出线段而不是三角形。
1.4 视口(Viewport)
OpenGL渲染窗口的尺寸大小,即视口(Viewport),通过调用glViewport函数来设置窗口的维度(Dimension):OpenGL幕后使用glViewport中定义的位置和宽高进行2D坐标的转换,将OpenGL中的位置坐标转换为你的屏幕坐标。
glViewport(0, 0, 800, 600); # 前两个参数控制窗口左下角的位置。第三个和第四个参数控制渲染窗口的宽度和高度(像素)
1.5 渲染(Render):从3D点云到屏幕图像的过程
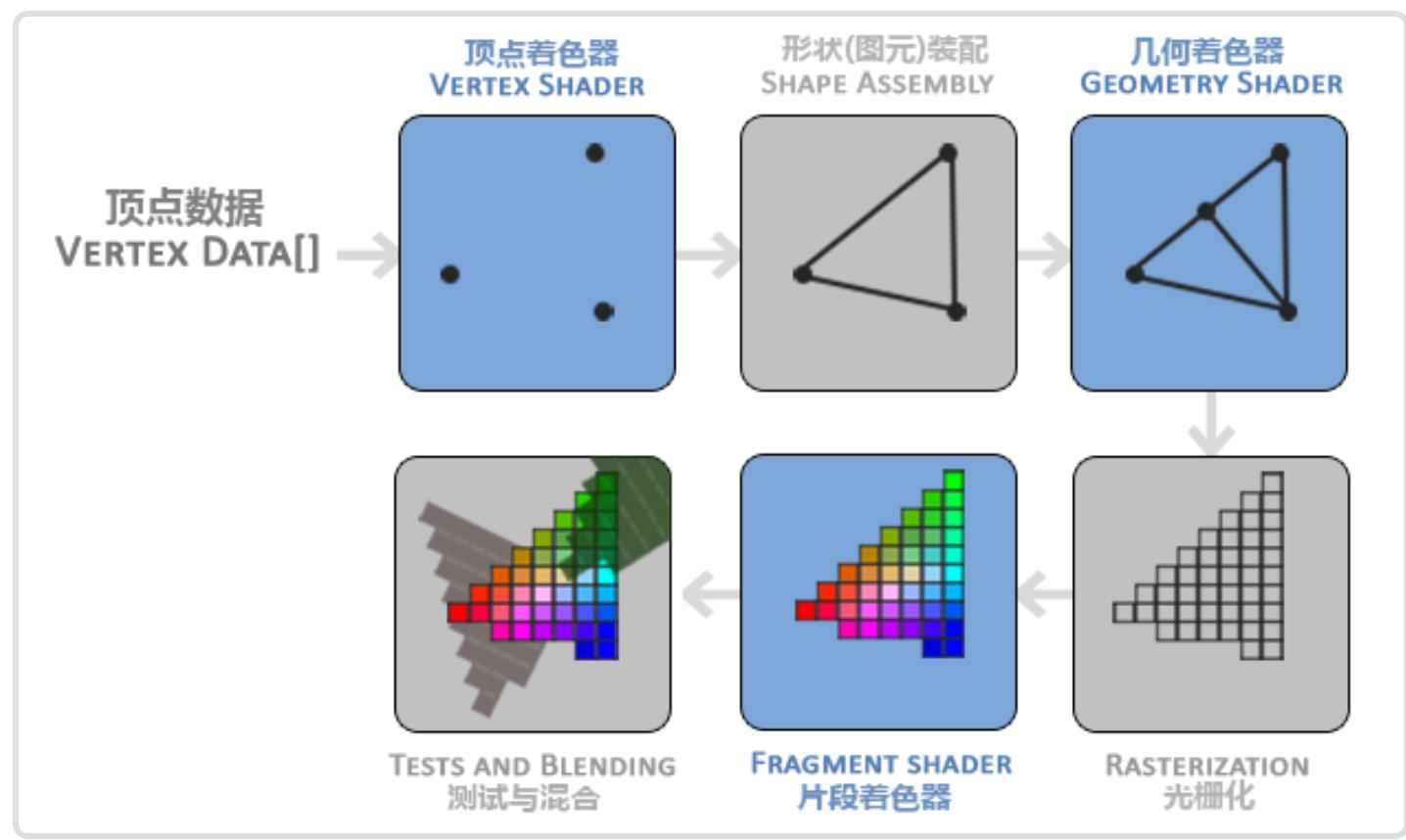
在OpenGL中,任何事物都在3D空间中,而屏幕和窗口却是2D像素数组,这导致OpenGL的大部分工作都是关于把3D坐标转变为适应你屏幕的2D像素。3D坐标转为2D坐标的处理过程是由OpenGL的图形渲染管线(Graphics Pipeline,大多译为管线,实际上指的是一堆原始图形数据途经一个输送管道,期间经过各种变化处理最终出现在屏幕的过程)管理的。
图形渲染管线可以被划分为两个主要部分:
-
第一部分把你的3D坐标转换为2D坐标,
-
第二部分是把2D坐标转变为实际的有颜色的像素。
1.6 着色器(Shader):处理数据的程序
图形渲染管线可以被划分为几个阶段,每个阶段将会把前一个阶段的输出作为输入。所有这些阶段都是高度专门化的(它们都有一个特定的函数),并且很容易并行执行。正是由于它们具有并行执行的特性,当今大多数显卡都有成千上万的小处理核心,它们在GPU上为每一个(渲染管线)阶段运行各自的小程序,从而在图形渲染管线中快速处理你的数据。这些小程序叫做着色器(Shader)。OpenGL着色器是用OpenGL着色器语言(OpenGL Shading Language, GLSL)写成的
- 顶点数据 Vertex Data
顶点数据(Vertex Data):以数组的形式传递3个3D坐标作为图形渲染管线的输入,用来表示一个三角形,这个数组叫做顶点数据(Vertex Data);顶点数据是一系列顶点的集合。一个顶点(Vertex)是一个3D坐标的数据的集合。
- 顶点属性(Vertex Attribute):
而顶点数据是用顶点属性(Vertex Attribute)表示的,它可以包含任何我们想用的数据,比如每个顶点由一个3D位置和一些颜色值组成
- 图元(Primitive)
为了让OpenGL知道我们的坐标和颜色值构成的到底是什么**,OpenGL需要你去指定这些数据所表示的渲染类型**。我们是希望把这些数据渲染成一系列的点?一系列的三角形?还是仅仅是一个长长的线?做出的这些提示叫做图元(Primitive),任何一个绘制指令的调用都将把图元传递给OpenGL。这是其中的几个:GL_POINTS、GL_TRIANGLES、GL_LINE_STRIP
2 基本内容

2.1 顶点输入
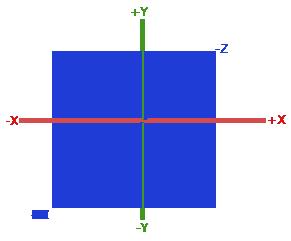
开始绘制图形之前,我们必须先给OpenGL输入一些顶点数据。OpenGL是一个3D图形库,所以我们在OpenGL中指定的所有坐标都是3D坐标(x、y 和 z)。OpenGL仅当3D坐标在3个轴(x、y和z)上都为[-1.0,1.0]的范围内时才处理它。所有在所谓的标准化设备坐标范围内的坐标才会最终呈现在屏幕上
屏幕坐标系,(0, 0)坐标是这个图像的中心,而不是左上角
X轴朝右
Y轴朝上
Z轴指向您后面,通常深度可以理解为z坐标,它代表一个像素在空间中和你的距离
由于我们希望渲染一个三角形,我们一共要指定三个顶点,每个顶点都有一个3D位置。定义为一个float数组。
float vertices[] =
-0.5f, -0.5f, 0.0f,
0.5f, -0.5f, 0.0f,
0.0f, 0.5f, 0.0f
;
1、标准化设备坐标——>屏幕空间坐标:glViewport视口变换(Viewport Transform)完成的。
2、屏幕空间坐标——>变换为片段——>片段着色器
2.2 顶点着色器(Vertex Shader)
作用是坐标变换,输出经过转化之后的位置坐标
我们需要做的第一件事是用着色器语言GLSL(OpenGL Shading Language)编写顶点着色器。
输入:顶点坐标
输出:坐标gl_Position和其它属性 vec4(),四维坐标
attribute vec3 position; // 点云空间坐标
void main()
gl_Position = vec4(scale * position,1.0);// 注意最后一个分量是用在透视除法(Perspective Division)上。
相关变量
uniform:一致变量,全局变量,对所有顶点或片断都一样
attribute:顶点属性,每顶点不同
varying:可变变量,用于顶点、片断着色器间传递自定义数据,在图元装配和光栅化过程,varying变量会被插值处理
uniform float scale; attribute vec2 position; attribute vec4 color; varying vec4 v_color; void main() gl_Position = vec4(position, 0.0, 1.0); v_color = color;
2.3 片段着色器(Fragment Shader)
片段着色器所做的是计算像素最后的颜色输出。在计算机图形中颜色被表示为有4个元素的数组:红色、绿色、蓝色和alpha(透明度)分量,通常缩写为RGBA。每个颜色分量的强度设置在[0.0,1.0]之间。
片段着色器需要一个
vec4颜色输出变量,因为片段着色器需要生成一个最终输出的颜色。如果你在片段着色器没有定义输出颜色,OpenGL会把你的物体渲染为黑色(或白色)。uniform是全局变量,我们可以在任何着色器中定义它们,而无需通过顶点着色器作为中介。
uniform vec4 color;
void main()
// 片段着色器只需要一个输出变量,这个变量是一个4分量向量,它表示的是最终的输出颜色
gl_FragColor = color;
2.4 着色器程序(Program)
着色器链接为一个着色器程序对象,然后在渲染对象的时候激活这个着色器程序。已激活着色器程序的着色器将在我们发送渲染调用的时候被使用。我们必须在渲染前指定OpenGL该如何解释顶点数据,对应最后一个参数。为了让OpenGL知道我们的坐标和颜色值构成的到底是什么**,OpenGL需要你去指定这些数据所表示的渲染类型**。做出的这些提示叫做图元(Primitive)
gloo.Program(vertex, fragment, count=len(self.xyz)).draw(gl.GL_QUADS)
2.5 纹理
纹理是一个2D图片,它可以用来添加物体的细节;你可以想象纹理是一张绘有砖块的纸,无缝折叠贴合到你的3D的房子上,这样你的房子看起来就像有砖墙外表了。因为我们可以在一张图片上插入非常多的细节,这样就可以让物体非常精细而不用指定额外的顶点。
为了能够把纹理映射到三角形上,我们需要指定三角形的每个顶点各自对应纹理的哪个部分。这样每个顶点就会关联着一个纹理坐标,用来标明该从纹理图像的哪个部分采样。之后在图形的其它片段上进行片段插值(Fragment Interpolation)
加载纹理
使用纹理之前要做的第一件事是把它们加载到我们的应用中。正确地加载图像并生成一个纹理对象,在渲染之前先把它绑定到合适的纹理单元上:
earthTexture_01 = np.array(Image.open(".//resources//image//世界地图4.jpg"))
GPU上传上传点云纹理坐标、纹理图像
program = gloo.Program(vertex, fragment, count=len(xyz))
program['texture'] = texture
代码中实现,在球类里面已经计算了纹理坐标
def sphere(r=1.0, m=100, n=100):
"""
计算球面点云坐标和纹理坐标
:param r: 半径
:param m: 经线数
:param n: 纬线数
:return: 坐标和纹理坐标
"""
t = np.linspace(0, np.pi, m)
p = np.linspace(0, 2 * np.pi, n)
positions = []
tex_positions = []
normal = []
for i in range(m - 1):
for j in range(n - 1):
x = r * np.sin(t[i]) * np.cos(p[j])
y = r * np.sin(t[i]) * np.sin(p[j])
z = r * np.cos(t[i])
positions.append([x, y, z])
tex_positions.append([p[j] / np.pi / 2, t[i] / np.pi]) # 就相当于把整个图片按长分成2pi份,按高分成pi份
x = r * np.sin(t[i + 1]) * np.cos(p[j])
y = r * np.sin(t[i + 1]) * np.sin(p[j])
z = r * np.cos(t[i + 1])
positions.append([x, y, z])
tex_positions.append([p[j] / np.pi / 2, t[i + 1] / np.pi])
x = r * np.sin(t[i + 1]) * np.cos(p[j + 1])
y = r * np.sin(t[i + 1]) * np.sin(p[j + 1])
z = r * np.cos(t[i + 1])
positions.append([x, y, z])
tex_positions.append([p[j + 1] / np.pi / 2, t[i + 1] / np.pi])
x = r * np.sin(t[i]) * np.cos(p[j + 1])
y = r * np.sin(t[i]) * np.sin(p[j + 1])
z = r * np.cos(t[i])
positions.append([x, y, z])
tex_positions.append([p[j + 1] / np.pi / 2, t[i] / np.pi])
positions = np.array(positions)
tex_positions = np.array(tex_positions)
normal = np.array(positions)
return positions, tex_positions, normal
3 坐标变换
3.1 矩阵运算
3.1.1 向量相乘
两个向量相乘是一种很奇怪的情况。普通的乘法在向量上是没有定义的,因为它在视觉上是没有意义的。但是在相乘的时候我们有两种特定情况可以选择:一个是点乘(Dot Product),记作v¯⋅k¯v¯⋅k¯,另一个是叉乘(Cross Product),记作v¯×k¯v¯×k¯。
点乘
两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。可能听起来有点费解,我们来看一下公式:
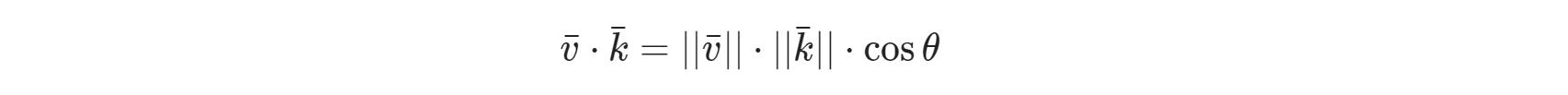
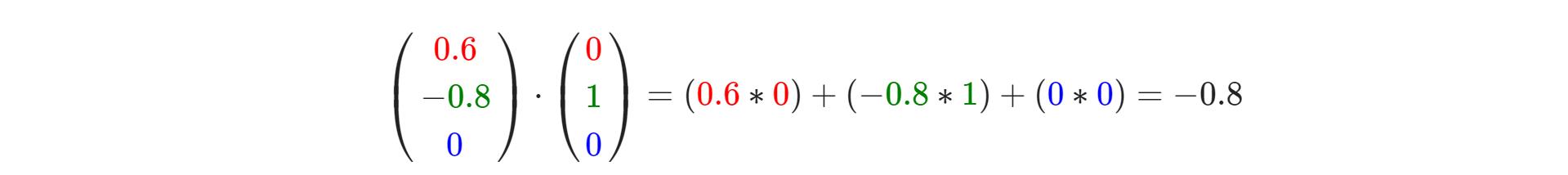
那么要计算两个单位向量间的夹角,我们可以使用反余弦函数cos−1 ,可得结果是143.1度。现在我们很快就计算出了这两个向量的夹角。点乘会在计算光照的时候非常有用。
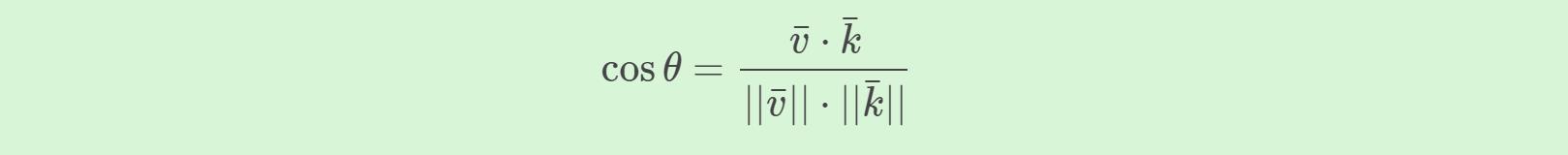
叉乘
叉乘只在3D空间中有定义,它需要两个不平行向量作为输入,**生成一个正交于两个输入向量的第三个向量。**如果输入的两个向量也是正交的,那么叉乘之后将会产生3个互相正交的向量。接下来的教程中这会非常有用。下面的图片展示了3D空间中叉乘的样子:
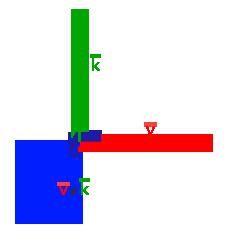
两个正交向量A和B叉积,输出得到一个正交于两个输入向量的第三个向量

3.1.2 矩阵
数乘

现在我们也就能明白为什么这些单独的数字要叫做**标量(Scalar)了。简单来说,标量就是用它的值缩放(Scale)**矩阵的所有元素,上面中所有的元素都被放大了2倍。
单位矩阵
这种变换矩阵使一个向量完全不变:

缩放矩阵
如果我们把缩放变量表示为(S1,S2,S3)我们可以为任意向量(x,y,z)定义一个缩放矩阵:

位移矩阵
对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为(Tx,Ty,Tz),我们就能把位移矩阵定义为:这才是把3维坐标变成四维坐标的原因:方便对左边通过矩阵进行平移操作,有了位移矩阵我们就可以在3个方向(x、y、z)上移动物体,它是我们的变换工具箱中非常有用的一个变换矩阵。

旋转矩阵
在3D空间中旋转需要定义一个角和一个旋转轴(Rotation Axis)。物体会沿着给定的旋转轴旋转特定角度。使用三角学,给定一个角度,可以把一个向量变换为一个经过旋转的新向量。这通常是使用一系列正弦和余弦函数(一般简称sin和cos)各种巧妙的组合得到的。.转半圈会旋转360/2 = 180度,向右旋转1/5圈表示向右旋转360/5 = 72度。


矩阵的转置

矩阵的逆
3.2 坐标运算
为了将坐标从一个坐标系变换到另一个坐标系,我们需要用到几个变换矩阵,最重要的几个分别是模型(Model)、观察(View)、投影(Projection)三个矩阵。

-
局部坐标:以对象自己为中心,是对象相对于局部原点的坐标。
-
世界空间坐标:物体在一个更大的空间所处的坐标,可以确定与其他物体的相对位置,和其它物体一起相对于世界的原点进行摆放。
-
**观察空间坐标:以观察者为坐标,使得每个坐标都是从摄像机或者说观察者的角度进行观察的。**确定对于观察者来讲的相对位置关系
-
**投影坐标:**投影到裁剪坐标。裁剪坐标会被处理至-1.0到1.0的范围内,并判断哪些顶点将会出现在屏幕上。
-
**视口变换:**将裁剪坐标变换为屏幕坐标,视口变换将位于-1.0到1.0范围的坐标变换到由glViewport函数所定义的坐标范围内。最后变换出来的坐标将会送到光栅器,将其转化为片段。
例如,当需要对物体进行修改的时候,在局部空间中来操作会更说得通;
如果要对一个物体做出一个相对于其它物体位置的操作时,在世界坐标系中来做这个才更说得通。
3.2.1 局部空间
局部空间是指物体所在的坐标空间,即对象最开始所在的地方。想象你在一个建模软件(比如说Blender)中创建了一个立方体。你创建的立方体的原点有可能位于(0, 0, 0),你的模型的所有顶点都是在局部空间中:它们相对于你的物体来说都是局部的。
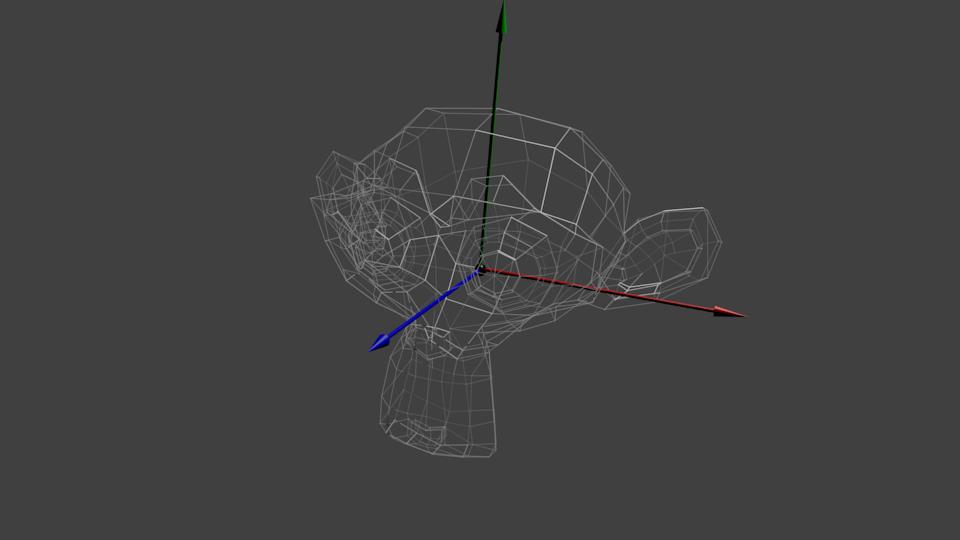
3.2.2 模型矩阵:局部——世界坐标
如果我们将我们所有的物体导入到程序当中,它们有可能会全挤在世界的原点(0, 0, 0)上,我们想为每一个物体定义一个位置,从而能在更大的世界当中放置它们。这就是你希望物体变换到的空间。物体的坐标将会从局部变换到世界空间;该变换是由模型矩阵(Model Matrix)实现的。
模型矩阵是一种变换矩阵,它能通过对物体进行位移、缩放、旋转来将它置于它本应该在的位置或朝向。
你可以将它想像为变换一个房子,你需要先将它缩小(它在局部空间中太大了),并将其位移至郊区的一个小镇,然后在y轴上往左旋转一点以搭配附近的房子。你也可以把上一节将箱子到处摆放在场景中用的那个矩阵大致看作一个模型矩阵;我们将箱子的局部坐标变换到场景/世界中的不同位置。

glm.translate(m, self.orbit[0], self.orbit[1], self.orbit[2]) # 公转,
# translate表示瞬时坐标的位移变换经过怎样的变换能得到单位矩阵,而这个返回的变换矩阵就是就得到模型矩阵
# 所以求model矩阵的思路是,算出局部坐标的瞬时位置,反推局部——世界的位移矩阵
# glm::translate() 创建一个位移矩阵,第一个参数是目标矩阵,第二个参数是位移的方向向量
# 返回的矩阵是能实现位移的矩阵,
3.2.3 视图矩阵:世界——观察坐标
观察空间就是从摄像机的视角所观察到的空间。而这通常是由一系列的位移和旋转的组合来完成,平移/旋转场景从而使得特定的对象被变换到摄像机的前方。这些组合在一起的变换通常存储在一个观察矩阵(View Matrix)里,它被用来将世界坐标变换到观察空间。

3.2.4 投影矩阵:观察——裁剪空间坐标
为了将顶点坐标从观察变换到裁剪空间,我们需要定义一个投影矩阵(Projection Matrix),它指定了一个范围的坐标,比如在每个维度上的-1000到1000。投影矩阵接着会将在这个指定的范围内的坐标变换为标准化设备坐标的范围(-1.0, 1.0)。所有在范围外的坐标不会被映射到在-1.0到1.0的范围之间,所以会被裁剪掉
3.2.5 正射投影
效果不真实
定义了可见的坐标,它由由宽、高、近(Near)平面和远(Far)平面所指定。任何出现在近平面之前或远平面之后的坐标都会被裁剪掉。正射平截头体直接将平截头体内部的所有坐标映射为标准化设备坐标,因为每个向量的w分量都没有进行改变;如果w分量等于1.0,透视除法则不会改变这个坐标

3.2.6 透视投影
透视(Perspective):离你越远的东西看起来更小。

OpenGL要求所有可见的坐标都落在-1.0到1.0范围内,作为顶点着色器最后的输出,顶点坐标的每个分量都会除以它的w分量,距离观察者越远顶点坐标就会越小。这是也是w分量非常重要的另一个原因,它能够帮助我们进行透视投影。最后的结果坐标就是处于标准化设备空间中的。

创建了一个定义了可视空间的大平截头体,它的第一个参数定义了fov的值,它表示的是视野(Field of View),并且设置了观察空间的大小。如果想要一个真实的观察效果,它的值通常设置为45.0f。第二个参数设置了宽高比,由视口的宽除以高所得。第三和第四个参数设置了平截头体的近和远平面。我们通常设置近距离为0.1f,而远距离设为100.0f。所有在近平面和远平面内且处于平截头体内的顶点都会被渲染。

perspective 函数使用
glm::perspective(float fovy, float aspect, float zNear, float zFar);
-
第一个参数为视锥上下面之间的夹角
-
第二个参数为宽高比,即视窗的宽/高
-
第三第四个参数分别为近截面和远界面的深度
glm.perspective(P_cam.alpha, 0.5 * W / float(H), 1, 300000.0)
def perspective(fovy, aspect, znear, zfar):
"""Create perspective projection matrix
Parameters
----------
fovy : float
The field of view along the y axis.
aspect : float
Aspect ratio of the view.
znear : float
Near coordinate of the field of view.
zfar : float
Far coordinate of the field of view.
所以整体的坐标变换就是这样

uniform float scale; // 模型缩放因子
uniform mat4 model; // 模型矩阵
uniform mat4 view; // 视图矩阵
uniform mat4 projection; // 投影矩阵
uniform mat4 viewport; // 视口矩阵
attribute vec3 position; // 点云空间坐标
void main()
gl_Position = viewport * projection * view * model * vec4(scale * position,1.0);
3.3 摄像机
当我们讨论摄像机/观察空间(Camera/View Space)的时候,是在讨论以摄像机的视角作为场景原点时场景中所有的顶点坐标:观察矩阵把所有的世界坐标变换为相对于摄像机位置与方向的观察坐标。要定义一个摄像机,我们需要创建一个三个单位轴相互垂直的、以摄像机的位置为原点的坐标系。

摄像机位置
摄像机位置简单来说就是世界空间中一个指向摄像机位置的向量。不要忘记正z轴是从屏幕指向你的,如果我们希望摄像机向后移动,我们就沿着z轴的正方向移动。
Z0 = 200
eyeAt = np.array([0, 0, Z0])
摄像机方向
指的是摄像机指向哪个方向。让摄像机指向场景原点:(0, 0, 0)。
用场景原点向量减去摄像机位置向量的结果就是摄像机的指向向量。由于我们知道摄像机指向z轴负方向,但我们希望方向向量(Direction Vector)指向摄像机的z轴正方向。如果我们交换相减的顺序,我们就会获得一个指向摄像机正z轴方向的向量:
lookAt = np.array([0, 0, 0])
# cam - target 就是获得的摄像机方向
方向向量(Direction Vector)并不是最好的名字,因为它实际上指向从它到目标向量的相反方向(译注:注意看前面的那个图,蓝色的方向向量大概指向z轴的正方向,与摄像机实际指向的方向是正好相反的)。
右轴
它代表摄像机空间的x轴的正方向。把上向量和第二步得到的方向向量进行叉乘。两个向量叉乘的结果会同时垂直于两向量,因此我们会得到指向x轴正方向的那个向量
glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f);
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));
上轴
一个指向摄像机的正y轴向量,现在我们已经有了x轴向量和z轴向量,获取一个指向摄像机的正y轴向量就相对简单了:我们把右向量和方向向量进行叉乘:
eyeUp = np.array([0, 1, 0])
3.3.1 Look At
将所有坐标变换到摄像机的视图矩阵
现在我们有了3个相互垂直的轴和一个定义摄像机空间的位置坐标,用矩阵来表示这个坐标轴,用这个矩阵乘以任何向量来将其变换到那个坐标空间。这正是LookAt矩阵所做的

其中R是右向量,U是上向量,D是方向向量,P是摄像机位置向量。注意,位置向量是相反的,因为我们最终希望把世界平移到与我们自身移动的相反方向。**把这个LookAt矩阵作为观察矩阵可以很高效地把所有世界坐标变换到刚刚定义的观察空间。**LookAt矩阵就像它的名字表达的那样:它会创建一个看着(Look at)给定目标的观察矩阵。
def view(cam, tar, u): #u是上
"""
计算视图矩阵:将世界坐标系的坐标变换到观察坐标系,也就是相机的视图当中
"""
cam = np.array(cam, np.float32)
tar = np.array(tar, np.float32)
u = np.array(u, np.float32)
f = tar - cam # 摄像机方向,从原点指向摄像机的坐标
f = f/np.linalg.norm(f) # 求求二范数,也就是模长
u = u/np.linalg.norm(u)
s = np.cross(f, u) # 返回两个向量的叉积。 得到摄像机坐标的右轴
u = np.cross(s, f) # 得到摄像机坐标的上轴
R = np.array([[ s[0], s[1], s[2], 0], # R代表三维坐标轴
[ u[0], u[1], u[2], 0],
[-f[0],-f[1],-f[2], 0],
[ 0, 0, 0, 1]
])
T = np.array([[ 1, 0, 0, -cam[0]], # T代表相机的坐标
[ 0, 1, 0, -cam[1]],
[ 0, -0, 1, -cam[2]],
[ 0, 0, 0, 1]
])
v2 = np.matmul(R, T) # 矩阵相乘既得到了lookAt矩阵也就是我们的观察矩阵
v2 = np.transpose(v2) # 转置,行变列
return v2
在代码中,我们是将LookAt矩阵直接赋值给view矩阵的,然后把view传递到vertex shader中。那么view矩阵是干嘛的呢?view是负责把世界坐标系转换成用摄像机的视角所观察到的坐标系当中。
LookAt
快速构建摄像机坐标系的方法(构建结果就是这个LookAt矩阵)
坐标系空间变换方法(世界空间->观察空间)。用LookAt矩阵左乘某向量X,就可以将X从世界空间变换到观察空间。
3.3.2 欧拉角
欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值,俯仰角是描述我们如何往上或往下看的角,可以在第一张图中看到。第二张图展示了偏航角,偏航角表示我们往左和往右看的程度。滚转角代表我们如何翻滚摄像机,通常在太空飞船的摄像机中使用。每个欧拉角都有一个值来表示,把三个角结合起来我们就能够计算3D空间中任何的旋转向量了。
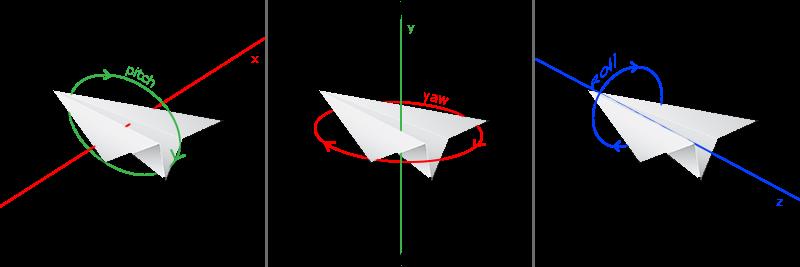
对于我们的摄像机系统来说,我们只关心俯仰角和偏航角,所以我们不会讨论滚转角。给定一个俯仰角和偏航角,我们可以把它们转换为一个代表新的方向向量的3D向量。我们可以看到x分量取决于cos(yaw)的值,z值同样取决于偏航角的正弦值。这样我们就有了一个可以把俯仰角和偏航角转化为用来自由旋转视角的摄像机的3维方向向量了。
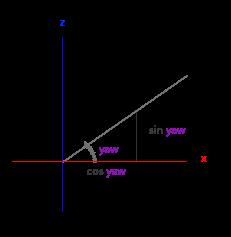
# 设置视点位置和方向
Z0 = 200
eyeAt = np.array([0, 0, Z0]) # cam
lookAt = np.array([0, 0, 0]) # 目标卫星
eyeUp = np.array([0, 1, 0]