背包问题

Posted 2022-02-02 萌萌滴太阳

文章目录

• 0-1背包问题
• 完全背包问题
• 多重背包问题
• • 多重背包问题1
  • 多重背包问题2
• 组合背包问题
• • 组合
  • 排列
• dp数组初始化问题
• 背包问题 代码模板和leetcode相关例题

参考

0-1背包问题

一件物品，只有选和不选两种情况，也就是每件物体，最多选一次；

优化空间。

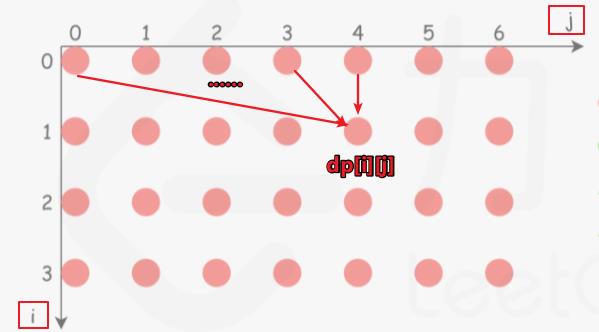
if(v[i] <= j)
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j - v[i]])

由上图的和动态方程得：第i行的dp[j]由上一行（第i-1行）的dp[j]和上一行（第i-1行）的dp[j]之前的dp[0，...，j-1]之间的一个共同确定；

即第i行由第i-1行唯一确定【因为第i个物品，要么不选，要么就选一个，不管什么情况，都从前i-1个物体的状态转移过来】，所以可以用滚动数组优化空间；dp[j] = Math.max(dp[j] , dp[j - v[i]])；

但第i行的dp[j]需要用到上一行（第i-1行）的dp[j]之前的dp[0，...，j-1]之间的一个来帮助确定，若从左向右计算；会把第i-1行的dp[j]转换成第i行的dp[j]，但后面的dp[j]计算需要用到前面第i-1行的dp[j]，可是此时前面第i-1行的dp[j]已变成前面第i行的dp[j]，所以出错；解决办法，从右向前计算即可；

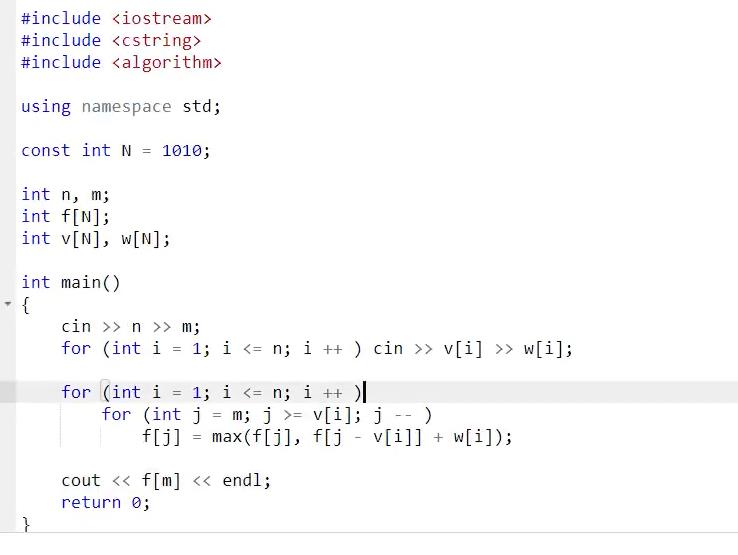
完全背包问题

每件物体被选的次数不受限制；
0-1背包的扩展，所以从右向左计算

• 优化空间

动态方程
if(k*v[i] <= j)
dp[i][j] = Math.max(dp[i-1][j] , dp[i][j - k*v[i]] + k*w[i])

如果不选第i个物品，dp[i][j] = dp[i-1][j]；
如果  选第i个物品，dp[i][j] = dp[i][j - k*v[i]] + k*w[i]；之所以还是dp[i]，即从前i个物品里选，是因为每个物品可以选无限次，选了第i个，第i个还可以再选；

优化后的动态方程：dp[j] = Math.max(dp[j] , dp[j - v[i]] + w[i])

• 证明一：为什么从左向右计算，会把第i-1行的dp[j]转换成第i行的dp[j]

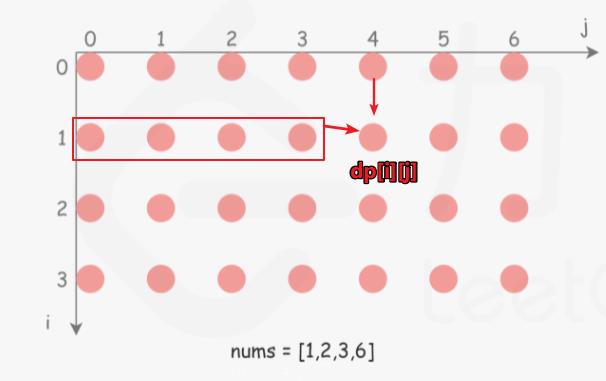
由下图的和动态方程得：第i行的dp[j]由上一行（第i-1行）的dp[j]和本行（第i行）的dp[j]之前的dp[0，...，j-1]之间的一个共同确定；

即第i行由第i-1和第i行确定【因为每个物品可以选无限次，选了第i个，第i个还可以再选；所以在选了第i个物体的前提下，dp[i][j]还是由前i个物体决定；另外不选第i个物体的情况不变，dp[i][j]还是由前i-1个物体决定】，

即，完全背包中，第i行的dp[j]需要用到本行（第i行）的dp[j]之前的dp[0，...，j-1]之间的一个来帮助确定，由0-1背包问题得，若从左向右计算；会把第i-1行的dp[j]转换成第i行的dp[j]（即，dp[j - v[i]]包含第i物体的结果），正好是我们需要的，所以完全背包的空间优化是从左向右计算；

• 证明二：为什么从左向右计算，dp[j] = Math.max(dp[j] , dp[j - v[i]] + w[i])可表示dp[i][j] = Math.max(dp[i-1][j] , dp[i][j - k*v[i]])中k的枚举

这部分参考

假设遍历到第i个物体，那我们求解的就是dp[i][0],dp[i][1],…,dp[i][V]
假设现在要求的j可以分解为x + kvi, 那dp[i][j] = dp[i][x + kvi];
正常来说

1. k是能选vi的最大个数，即满足k*vi<=j的K的最大值
2. dp[i-1][x+kvi]表示不选第i的物体
3. dp[i-1][x+(k-1)vi]表示选1个第i的物体
...
4. dp[i-1][x] = dp[i-1][x +（k-k）vi]表示选k个第i的物体

dp[i][j] = dp[i][x + kvi] = max(dp[i-1][x+kvi],dp[i-1][x+(k-1)vi] + wi,.., dp[i-1][x] + kwi)

那么同理

dp[i][x + (k-1)vi] = max(dp[i-1][x+(k-1)vi],.., dp[i-1][x] + （k-1）wi)

又

dp[i][x + kvi] = max(dp[i-1][x+kvi],max(dp[i-1][x+(k-1)vi] + wi,.., dp[i-1][x] + k*wi))

max(dp[i-1][x+(k-1)vi] + wi,.., dp[i-1][x] + kwi) = dp[i][x + (k-1)*vi] + wi

所以 推出

dp[i][x + k * vi] = max(dp[i-1][x + kvi],wi + dp[i][x + (k-1)vi])

所以

dp[i][j] = max(dp[i-1][j], wi + dp[i][j-vi])

把i去掉

dp[j] = max(dp[j],dp[j-vi] + wi)

所以必须从左往又遍历，因为 要求数组index >= 0, j - vi >= 0 -> j >= vi, j从vi开始遍历

多重背包问题

每件物体被选的次数有限制，且不同；

多重背包问题1

• 解析
  

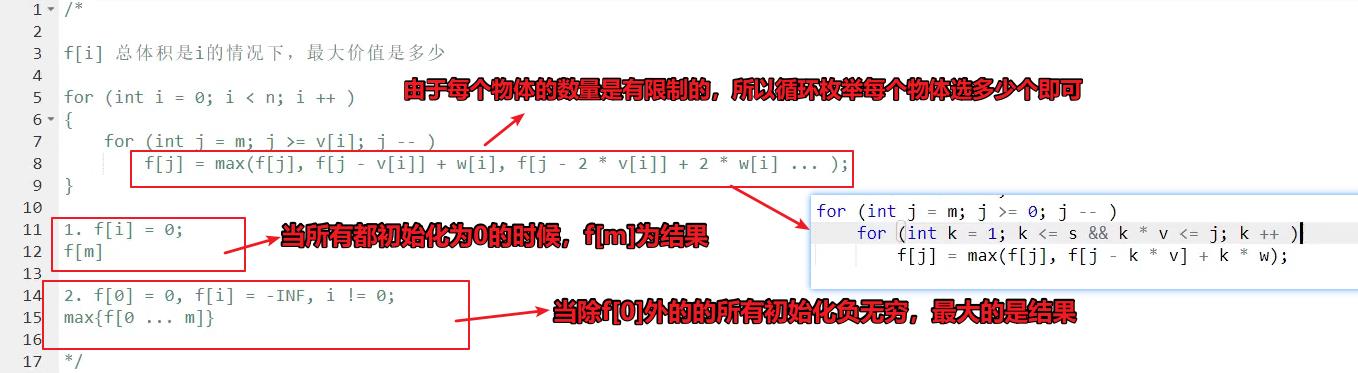
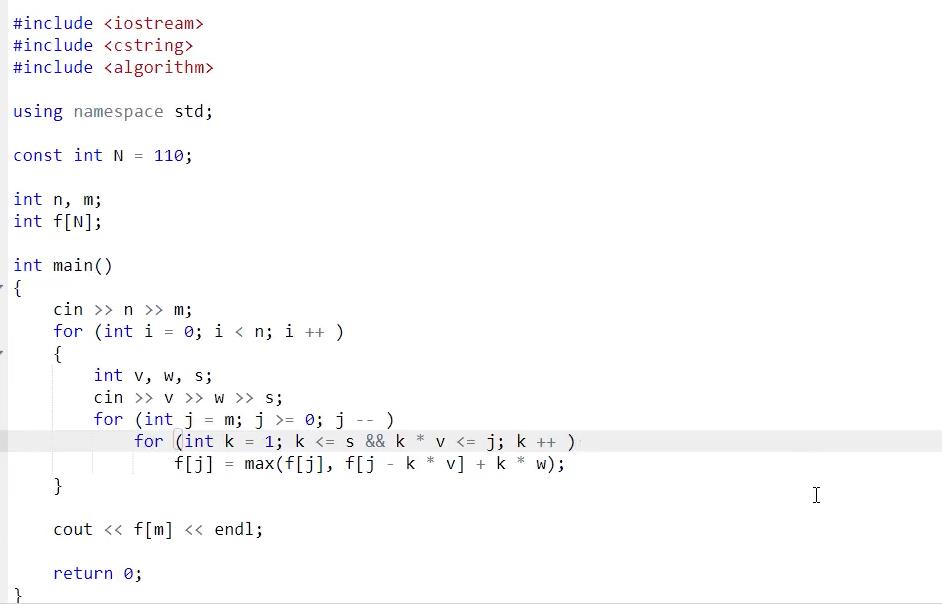
问题：3个循环，时间复杂度O(n^3)，复杂度太高；
多重背包问题2-----优化时间复杂度；

多重背包问题2

题目和多重背包问题1一样，只不过数据范围更大了，需要优化时间复杂度；

• 优化时间复杂度基本思想：转换为0-1背包问题；因为每个物品是有限个的，所以可以把每个物体拆开(比如物体k，体积vk，价值wk，有s个，则在原数组中将vk，wk重复s次)，放进原数组里，这样每个物体就只能选一次，变成0-1背包问题；

• 但这样拆太低级，时间复杂度还是较高；我们可以用二进制的方法拆分，拆成log2(s)份；把循环S的时间复杂度从O(S)降到O(og2(s))，比如S=1024，log2(s)=10，则时间复杂度从1024降到10；

• 二进制的方法拆分：
  比如7：log2(7)向上取整为3， 幂增长列举3个，1 2 4，它们组合可以得到1~7之间的所有数；
  但比如10，log2(10)向上取整为4，幂增长列举4个，1 2 4,8 ，它们组合可以得到1~15之间的所有数；
  但10~15中间的数我们不需要；所以我们一个一个的 幂增长， 幂增长一个就用S减去一个，直到S变为负的，将剩下的留下，比如S=10，S-1-2-4=3，再间8= -5，所以剩下的的是3，所以可以用1,2,4,3组合得到1~10中的任意数；

组合背包问题

参考

组合背包问题是0-1背包、完全背包的扩展，它涉及求组合数或排列数，涉及内外循环的顺序

• 纯完全背包求得是能否凑成总和，和凑成总和的元素有没有顺序没关系，即：有顺序也行，没有顺序也行！
• 若要求凑成总和的组合数，即，元素之间要求没有顺序。外层for循环遍历物品，内层for遍历背包容量。

for (int i = 0; i < coins.size(); i++)  // 遍历物品
    for (int j = coins[i]; j <= amount; j++)  // 遍历背包容量
        dp[j] += dp[j - coins[i]];
    

假设：coins[0] = 1，coins[1] = 5。
那么就是先把1加入计算，然后再把5加入计算，得到的方法数量只有1, 5这种情况。而不会出现5, 1的情况。

所以这种遍历顺序中dp[j]里计算的是组合数！

• 若要求凑成总和的排列数，即，元素之间要求有顺序。外层for遍历背包容量，内层for循环遍历物品；

for (int j = 0; j <= amount; j++)  // 遍历背包容量
    for (int i = 0; i < coins.size(); i++)  // 遍历物品
        if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
    

背包容量的每一个值，都是经过 1 和 5 的计算，包含了1, 5 和 5, 1两种情况。

此时dp[j]里算出来的就是排列数！

组合

排列

dp数组初始化问题

一般情况下：

• 求数量dp[j] += dp[j - coins[i]];
  dp[0]一定要为1，dp[0] = 1是 递归公式的基础。【至于dp[0] = 1 有没有意义呢？也不去强行解释它的意义，仅仅是为了推导递推公式。若要解释：dp[0]：凑成总金额0的货币组合数为1。】
  下标非0的dp[j]默认初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]

• 求最值dp[i] = max/min(dp[i], dp[i-nums]+1)或dp[i] = max/min(dp[i], dp[i-num]+nums);

• 求真假dp[j] = dp[j] || dp[j - coins[i]];

背包问题 代码模板和leetcode相关例题

参考1
参考2

参考3

参考4，含组合背包问题解析总结