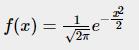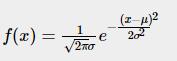视觉SLAM十四讲笔记 -- 第一讲

Posted 2022-02-01 炼丹狮

​

第一讲：课后习题

1. 有线性方程 Ax = b，若已知 A,b，需要求解x，该如何求解？ 这对 A 和 b 有哪些要求? 【提示:从A的维度和秩角度来分析】

答：可以利用大学时候学的非齐次方程组的方法求解，利用 A 的增广矩阵 ，对增广矩阵进行标准化和归一化。
A的增广矩阵是：
​​
rank(A)<rank(A~) ， 方程组 (2) 无解
rank(A)=rank(A~)=n ， 方程组 (2) 有唯一解
rank(A)=rank(A~)<n ， 方程组 (2) 有无穷解
rank(A)>rank(A~) 不可能出现， 因为增广矩阵的秩大于等于系数矩阵的秩（矩阵加入一列，其秩只能增大，不可能变小）

2. 高斯分布是什么? 它的一维形式是什么样子? 它的高维形式是什么样子?

答：高斯分布（Gaussian distribution），也称正态分布（Normal distribution），最早由棣莫弗（Abraham de Moivre）在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。
正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

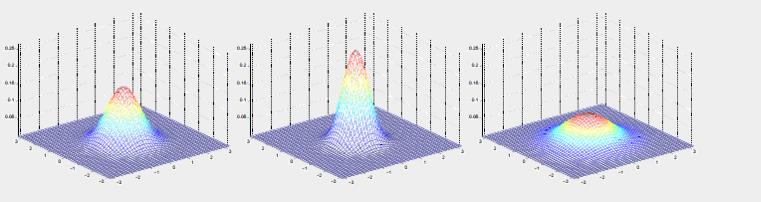
在数据建模时，经常会用到多元高斯分布模型，下面就这个模型的公式并结合它的几何意义，来做一个直观上的讲解。

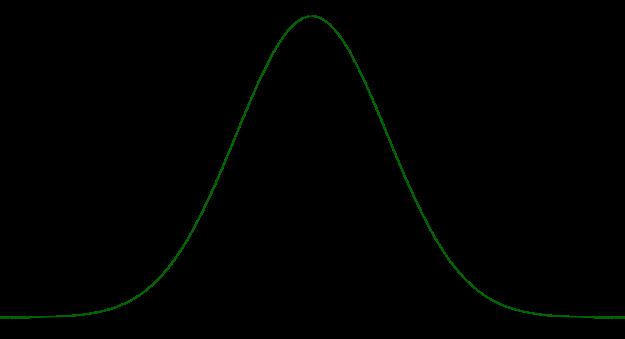
（1）标准高斯函数

高斯函数标准型：

这个函数描述了变量 x 的一种分布特性，变量x的分布有如下特点：
Ⅰ， 均值 = 0
Ⅱ， 方差为1
Ⅲ， 概率密度和为1

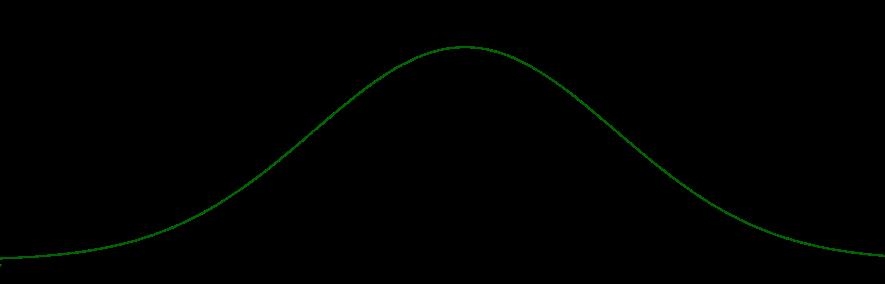
（2）一元高斯函数一般形式

一元高斯函数一般形式：

高维形式如下：

3. 你知道C++中的类吗? 你知道STL吗? 你使用过它们吗?

答：总共三个问题：
（1）你知道C++中的类吗?
C++ 是面向对象的语言，其中的类就是一种用户自己定义的数据类型、处理某个问题的单元。在一个类中，用户可以自己定义数据结构，可以自定义处理这些数据的业务逻辑。在面向对象的设计中，一般都是对外隐藏变量，通过接口来对外暴露处理逻辑或者变量的值，这样方便控制数据的权限。更多解释请参见：C++类的介绍
（2）你知道STL吗?
C++标准库由三组库构成：C库，C++库和标准模板库(STL)，STL包含了诸多在计算机科学领域里常用的基本数据结构和基本算法。详解请参见：STL学习小结
（3）你使用过它们吗?
使用过

4. 你以前怎样书写C++程序?（你完全可以说只在Visual C++6.0下写过CH+工程只要你有写C++和C语言的经验就行。)

答：写过，使用的开发工具是VS2019。写过一些封装硬件的c++接口，使用python调用这些接口。

5. 你知道C++11标准吗? 你听说过或用过其中哪些新特性? 有没有其他的标准

答：C++11 标准由国际标准化组织（ISO）和国际电工委员会（IEC）旗下的C++标准委员会（ISO/IEC JTC1/SC22/WG21）于2011年8月12日公布[2] ，并于2011年9月出版。2012年2月28日的国际标准草案(N3376)是最接近于C++11标准的草案（仅编辑上的修正）。此次标准为C++98发布后13年来第一次重大修正。
　　1.对C++核心语言的扩充
　　2.核心语言运行期的强化(右值引用和 move 语义;泛化的常数表达式;对POD定义的修正)
　　3.核心语言建构期表现的加强(外部模板)
　　4.核心语言使用性的加强(初始化列表;统一的初始化;类型推导[auto关键字];以范围为基础的 for 循环;Lambda函数与表示法;另一种的函数语法;对象构建的改良;显式虚函数重载;空指针;强类型枚举;角括号;显式类型转换;模板的别名;无限制的unions)
　　5.核心语言能力的提升(变长参数模板;新的字符串字面值;用户自定义的字面值;多任务存储器模型;thread-local的存储期限;使用或禁用对象的默认函数;long long int 类型;静态assertion;允许sizeof运算符作用在类型的数据成员上，无需明确的对象;)
　　6.C++标准程序库的变更(标准库组件的升级;线程支持;多元组类型;散列表;正则表达式;通用智能指针;可扩展的随机数功能;包装引用;多态函数对象包装器;用于元编程的类型属性;用于计算函数对象返回类型的统一方法)
详细可参见：C++11新标准

6. 你知道Linux吗?你有没有至少使用过一种（不算安卓）操作系统，比如 Ubuntu?

答：使用过RedHat，Ubuntu，CentOS这三种操作系统，用于程序服务器的部署，相关命令都相差不大

7. Linux的目录结构是什么样的? 你知道哪些基本命令，比如 Is,cat等?

答：Linux 是树形的目录结构，基本命令太多了，例如ls，ll，cd，mkdir，mv，du，df，ps等等

8. 如何在 Ubuntu系统中安装软件（不打开软件中心的情况下)? 这些软件被安装在什么地方? 如果只知道模糊的软件名称（比如想要装一个名称中含有Eigen 的库)，应该如何安装它?

答：（1）应该有三种方法来安装软件
第一种：使用apt-get install来安装应用程序
比如我要安装 nginx 这个软件，使用以下，他会帮我把所有的依赖包都一起安装了。例如： >sudo apt-get install nginx
常用命令：

• apt-get install xxx 安装xxx 。如果带有参数，那么-d 表示仅下载 ，-f 表示强制安装
• apt-get remove xxx 卸载xxx
• apt-get update 更新软件信息数据库
• apt-get upgrade 进行系统升级
• apt-cache search 搜索软件包

第二种：dpkg安装deb包
安装方法如下：
sudo dpkg -i package.deb
常用命令如下：

• dpkg -i package.deb 安装包
• dpkg -r package 删除包
• dpkg -P package 删除包（包括配置文件）
• dpkg -L package 列出与该包关联的文件
• dpkg -l package 显示该包的版本
• dpkg –unpack package.deb 解开 deb 包的内容
• dpkg -S keyword 搜索所属的包内容
• dpkg -l 列出当前已安装的包
• dpkg -c package.deb 列出 deb 包的内容
• dpkg –configure package 配置包

第三种：make install源代码安装
如果要使用make安装的话，那么必须得安装build-essential这个依赖包，安装方法已经在前面说过了。在安装完毕以后，我们就可以进行源码安装。源码安装大致可以分为三步骤：（./configure）–＞ 编译（sudo make） –＞ 安装（sudo make install）。
配置：这是编译源代码的第一步，通过 ./configure 命令完成。执行此步以便为编译源代码作准备。常用的选项有 --prefix=PREFIX，用以指定程序的安装位置。更多的选项可通过 --help 查询。也有某些程序无需执行此步。
编译：一旦配置通过，可即刻使用 make 指令来执行源代码的编译过程。视软件的具体情况而定，编译所需的时间也各有差异，我们所要做的就是耐心等候和静观其变。此步虽然仅下简单的指令，但有时候所遇到的问题却十分复杂。较常碰到的情形是程序编译到中途却无法圆满结束。此时，需要根据出错提示分析以便找到应对之策。
安装：如果编译没有问题，那么执行 sudo make install 就可以将程序安装到系统中了。


（2）模糊安装软件
如果只知道软件的模糊名称，可以
yum list | grep eigen
进行安装。

9. 花一个小时学习Vim，因为你迟早会用它。你可以在终端中输入vimtutor阅读一遍所有内容。我们不需要你非常熟练地操作它，只要能够在学习本书的过程中使用它输入代码即可。不要在它的插件上浪费时间，不要想着把Vim用成 IDE，我们只用它做文本编辑的工作。

答：比较熟悉Vim，平时对服务器端的运维操作都是通过这个来做的，基本命令比较熟悉。

参考文献：
[1].线性方程组的解
[2].多元高斯分布（The Multivariate normal distribution） - bingjianing - 博客园
[3].STL学习小结
[4].C++类的介绍

码字不易，欢迎点赞，评论，收藏 ，o(￣︶￣)o

​