基础知识彻底搞懂float16与float32的计算方式

Posted 2022-02-01 超级无敌陈大佬的跟班

参考链接：https://blog.csdn.net/leo0308/article/details/117398166

简单介绍：

深度学习中int8、float16、float32的主要却别在于能表示的数值范围、数值精度。

半精度是英伟达在2002年搞出来的，双精度和单精度是为了计算，而半精度更多是为了降低数据传输和存储成本。

很多场景对于精度要求也没那么高，例如分布式深度学习里面，如果用半精度的话，比起单精度来可以节省一半传输成本。考虑到深度学习的模型可能会有几亿个参数，使用半精度传输还是非常有价值的。

int8取值范围是：-128 - 127        精度：整数位

float16取值范围：-65504 ~ 65504        精度：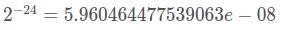

float32取值范围：-3.4*e38 ~ 3.4*e38        精度：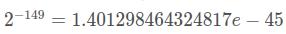

详细分析

1.1 float16

1.1.1 计算方式

float 16又称半精度， 用16个比特(2个字节)表示一个数。
如下图所示， 其中1位符号位， 5位指数位， 10位小数位。

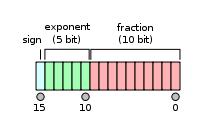
那么， 这16个比特位是怎么表示1个数的呢 ？ 分3部分：符号位 ， 指数部分， 小数部分。

• a 符号位： 1代表负数， 0代表正数。
• b 指数部分:5个比特位， 全0和全1有特殊用途，所以是00001~11110， 也就是1到30， 减去偏置15，指数部分最终范围为-14 ~15.
• c 小数部分：10个比特位， 范围为（0~1023）/1024.

所以最终一个数据的计算方式为：

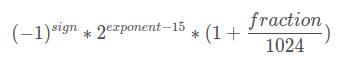
但是需要注意， 有2个特殊情况， 也就是上面说的指数位全0和全1的特殊用途。
1）exponent全0
计算公式为：

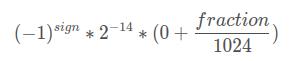
2）exponent全1
如果fraction全0 ， 则表示+inf或者−inf（范围的上界和下界）。
如果fraction不全为0 ， 则表示NaN。

1.1.2 表示范围与精度

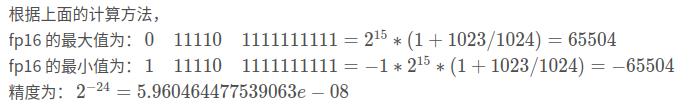
有效动态范围： 5.960464477539063e-08 ~ 65504 注意这里不是从最小值到最大值， 而是说的正数的部分， 因为正负是对称的。

另外， 需要注意的一点是， fp16表示的数的范围是非均匀的， 什么意思呢？ fp16表示的数的范围是-65536 - 65536， 但这些数并不是等间隔分布的。 在不同的区间， 间隔是不一样的， 最小的间隔为 2^-24 , 最大的间隔 2^5。

1.2 float32

1.2.1 计算方式

float32 又称单精度， 用32个比特数（4个字节）表示一个数。
如下图所示， 其中1位符号位， 8位指数位， 23位小数位。

那么， 这32个比特位是怎么表示1个数的呢 ？ 分3部分：符号位 ， 指数部分， 小数部分。

• a 符号位： 1代表负数， 0代表正数。
• b 指数部分：8个比特位， 全0和全1有特殊用途，所以是00000001~11111110， 也就是1到254， 减去偏置127，指数部分最终范围为-126 ~127.
• c 小数部分： 23个比特位， 范围为[(0 ~ 2^23) - 1] / 2^23

所以最终一个数据的计算方式为：

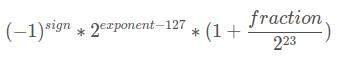
但是需要注意， 有2个特殊情况， 也就是上面说的指数位全0和全1的特殊用途。
1）exponent全0
计算公式为

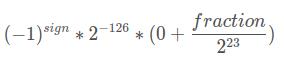
2）exponent全1
如果fraction全0 ， 则表示 +inf 或者 −inf。
如果fraction不全为0 ， 则表示 NaN。

1.2.2 表示范围与精度

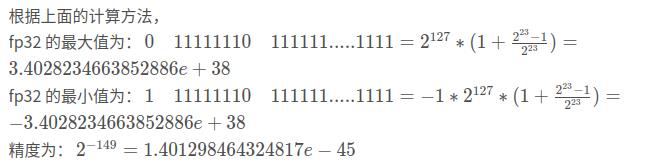
有效动态范围：1.401298464324817e-45 ~ 3.4028234663852886e+38 注意这里不是从最小值到最大值， 而是说的正数的部分， 因为正负是对称的。
同样地， fp32表示的数的范围是非均匀的. fp32表示的数的范围是-3.4028234663852886e+38 – 3.4028234663852886e+38， 但这些数并不是等间隔分布的。 在不同的区间， 间隔是不一样的， 最小的间隔为 2^-149 , 最大的间隔为 2^104。