挑战程序设计竞赛（算法和数据结构）——15.5最小生成树（Kruskal算法）的JAVA实现

Posted 2022-01-31 小乖乖的臭坏坏

题目和思路：

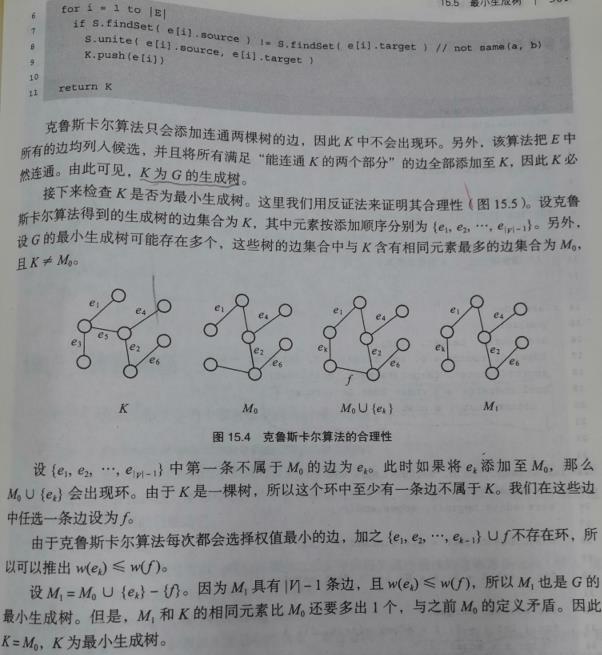
代码：

import java.util.Collections;
import java.util.Comparator;
import java.util.Scanner;
import java.util.Vector;

public class MinimumSpanningTree 
    public static void main(String[] args) 
        Scanner cin = new Scanner(System.in);
        int N = cin.nextInt();
        int M = cin.nextInt();
        Vector<Edge> edges = new Vector<>();
        for (int i=0;i<M;i++)
            int s = cin.nextInt();
            int t = cin.nextInt();
            int w = cin.nextInt();
            Edge e = new Edge(s, t, w);
            edges.add(e);
        
        System.out.println(kruskal(N, edges));
    

    static class UnionFindTree
        Vector<Integer> rank= new Vector<>();
        Vector<Integer> p= new Vector<>();

        //构造函数有无参构造和带参构造
        UnionFindTree()
        //带参构造 输入为容器尺寸
        UnionFindTree(int size)
            rank.setSize(size);//rank用于存放排名
            p.setSize(size);//p用于存放属于哪一个类
            //初始化
            for(int i=0;i<size;i++)makeSet(i);
        

        public void makeSet(int x)
            //将所有的rank初始化为0，将所有的p初始化为本身
            p.set(x, x);
            rank.set(x, 0);
        

        public boolean same(int x, int y)
            return findSet(x) == findSet(y);
        

        public int findSet(int x)
            if(x!=p.elementAt(x))//如果x的集合被合并了，那么p[x]的值就代表x当前属于第p[x]类，而p[x]值本身又代表属于一个类的头节点
                p.set(x,findSet(p.elementAt(x)));//那么就将头节点的值赋给p[x]（也许没用？？）
            
            return p.elementAt(x);//返回p[x]
        

        public void unite(int x, int y)
            //合并两个集合
            //将两个数所属的类别的头节点拿出来比较
            link(findSet(x), findSet(y));
        

        public void link(int x, int y)
            if(rank.elementAt(x)>rank.elementAt(y))//如果x的rank更大一些，那就把x的头节点的值赋给y（rank大，说明类大一些）
                p.set(y, x);
            
            else 
                p.set(x, y);//否则就会把y的头节点赋给x
                if(rank.elementAt(x)==rank.elementAt(y))//如果xy本身同属一类
                    rank.set(y,rank.elementAt(y)+1);//那么就让y的rank+1
                
            
        
    

    //定义一个边类型的类（数据结构）
    static class Edge
        public int source, target, cost;
        Edge(int source, int target, int cost)
            this.source = source;
            this.target = target;
            this.cost = cost;
        
    

    //直接走一遍kruskal算法，结果就出来了
    public static int kruskal(int N, Vector<Edge> edges)
        int totalCost = 0;//先定义总花销并初始化为0
        //排序
        Collections.sort(edges, new Comparator<Edge>() 
            @Override
            public int compare(Edge o1, Edge o2) 
                if(o1.cost<o2.cost)return -1;
                else if(o1.cost<o2.cost)return 1;
                else return 0;
            
        );

        //定义一个尺寸为N+1的并查集
        UnionFindTree dset = new UnionFindTree(N+1);

        for (int i=0;i<N;i++)
            dset.makeSet(i);//对每一个元素初始化并查集
        

        //由于每一条边已经根据从小到大的顺序进行排列
        for (int i=0;i<edges.size();i++)//对于每一条边来说
            Edge e = edges.elementAt(i);//将e标记为第i条边
            if(!dset.same(e.source, e.target))//如果一条边的两个端点不在同一个集合中，那就将这条边添加至同一个集合，cost增加
                //MST.push_back(e);
                totalCost += e.cost;
                dset.unite(e.source, e.target);
            
        
        return totalCost;
    

输入：

6 9
0 1 1
0 2 3
1 2 1
1 3 7
2 4 1
1 4 3
3 4 1
3 5 1
4 5 6

输出：

5