用高中的知识点徒手推导逻辑回归中的反向梯队

Posted 2022-01-31 MichaelIp

关于逻辑回归的梯队推导，我看到很多文章，题目写到这里时会说，根据到时微积分，我们可以得到

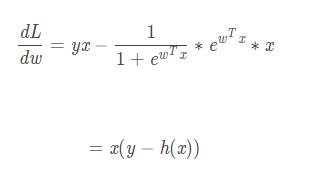
我认为不全面甚至有点跳跃，下面是我一步一步， 用高中的知识点推导出完整的梯度

知识点回顾：

导数公式（高中知识点）：

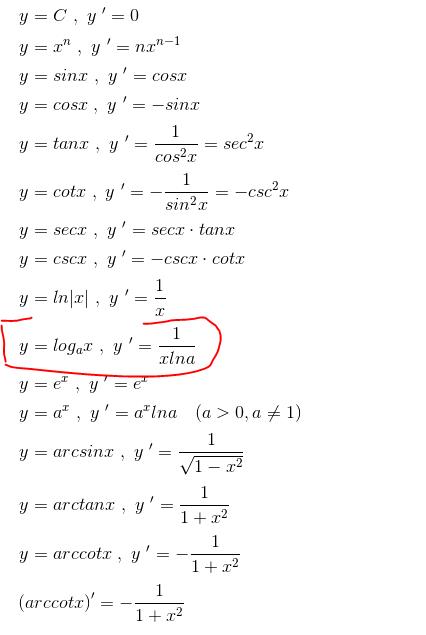
运算法则（高中知识点）：

减法法则：(f(x)-g(x))’=f’(x)-g’(x)

加法法则：(f(x)+g(x))’=f’(x)+g’(x)

乘法法则：(f(x)g(x))’=f’(x)g(x)+f(x)g’(x)

除法法则：(g(x)/f(x))’=(g’(x)f(x)-f’(x)g(x))/(f(x))^2

链式求导（大学知识点）：

我印象中链式求导高中就有学， 但查了下链式求导属于微积分， 高中不学，稍微超纲了一点，但这个知识点很好理解。
假设多个向量存在依赖关系，比如三个向量x→y→zx→y→z存在依赖关系，则我们有下面的链式求导法则：

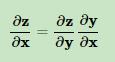
接下来温故下正向推导（以下所讲是未正则化的神经网络）

逻辑回归算法：

正向传递过程：

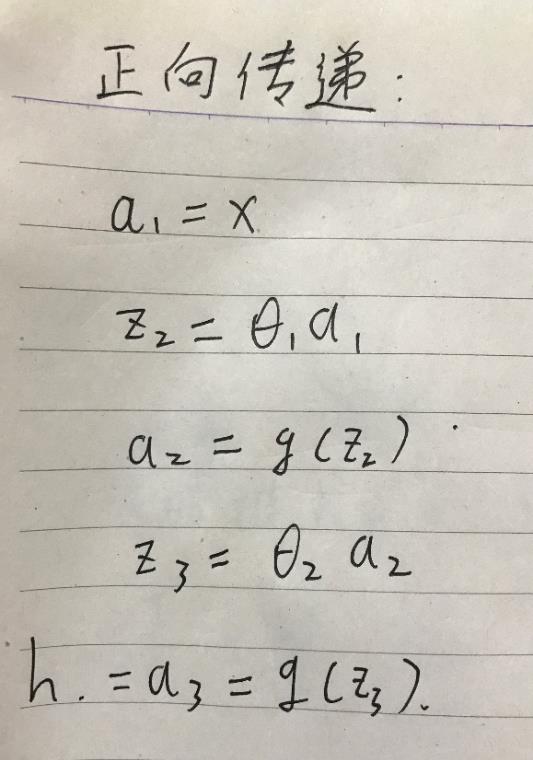
代价函数：

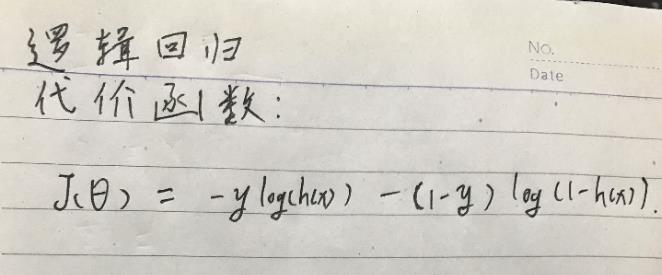
现在，我们需要根据上面的损失函数计算出第二梯度和第一梯度，根据Andrew Ng的推导：

Andrew Ng 这一推导我是有点难理解的，有点跳跃，下面根据我的理解，对损失函数进行第一梯度和第二梯度进行推导：

第二梯度：

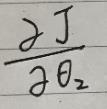
第一梯度：

根据链式求导法则，我们可以做出以下推导

这里我们开始求第二梯度， 下面是我一步一步推导：

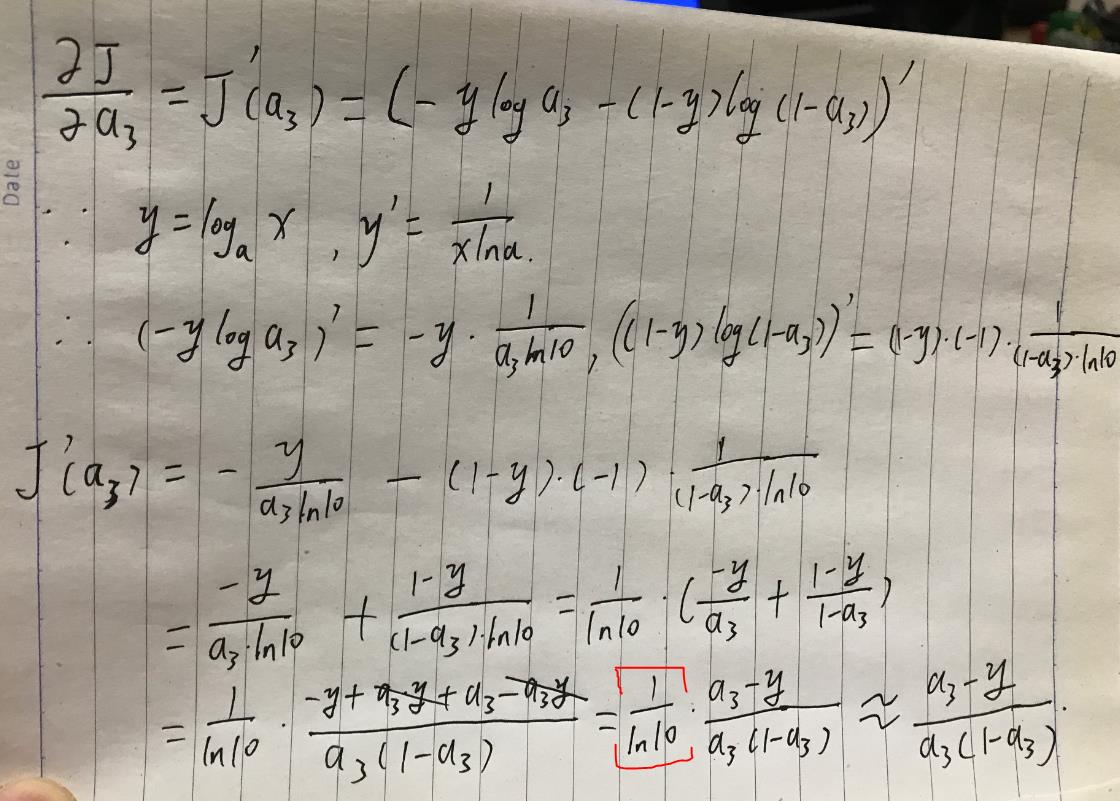
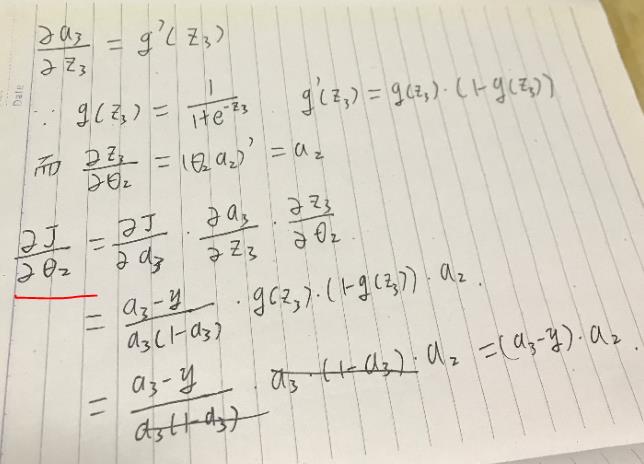
上面我把1/ln10 约等于1，这是关键，最后结果，第二梯度等于（a3-y）*a2，与Andrew Ng推导结果一致。说明1/ln10 等于1才能使（a3-y）*a2成立。

我觉得之所以把1/ln10 约等于1，只是方便计算，梯度只控制变化大小， 最后大小由学习率，而1/ln10只是一个参数，约掉只是方便理解和计算。

下面我们来求第一梯度

有了第二梯度的铺垫 ， 第一梯度显得相对简单。

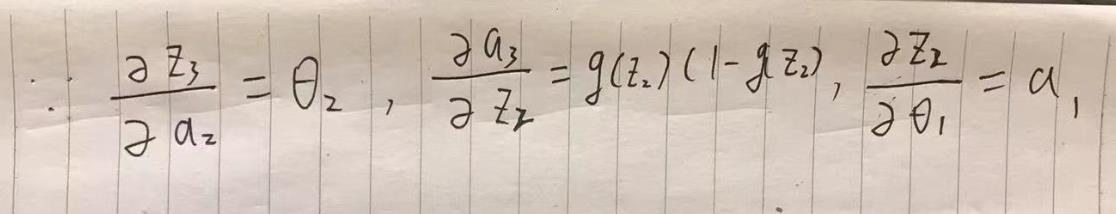
最后结果也和Andrew Ng推导的一致。
知其然更要知其然，谢谢观看， 欢迎指正。

Referrence:
https://www.cnblogs.com/pinard/p/10825264.html