内部排序常用算法(含动图及算法性能测试程序,了解不同情况下的排序算法的选择)
Posted 卖寂寞的小男孩
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了内部排序常用算法(含动图及算法性能测试程序,了解不同情况下的排序算法的选择)相关的知识,希望对你有一定的参考价值。
前言
本篇主要讲解内部排序的八种算法,及其中的递归实现以及非递归实现方法,并对各种算法进行性能测试,分析出对于不同数据性质最优的排序算法选择方式。并详细阐述每一种算法的代码设计思路。
算法的测试程序
使用TestOP函数对排序算法进行测试。
其基本原理为:1.向排序算法中输入相同的多的数据。
2.利用clock()函数标记排序算法的始末时间,然后作差。
void TestOP()
srand(time(0));
const int N = 100000;//输入十万个数据进行排序
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();//记录每一个算法的始末时间
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
SelectSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
QuickSort(a5, 0, N - 1);
int end5 = clock();
int begin6 = clock();
MergeSort(a6, N);
int end6 = clock();
int begin7 = clock();
BubbleSort(a7, N);
int end7 = clock();
printf("InsertSort:%d\\n", end1-begin1);//对始末时间作差得到算法执行时间
printf("ShellSort:%d\\n", end2 - begin2);
printf("SelectSort:%d\\n", end3 - begin3);
printf("HeapSort:%d\\n", end4 - begin4);
printf("QuickSort:%d\\n", end5 - begin5);
printf("MergeSort:%d\\n", end6 - begin6);
printf("BubbleSort:%d\\n", end7 - begin7);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
free(a7);
我们可以先看一看效果:
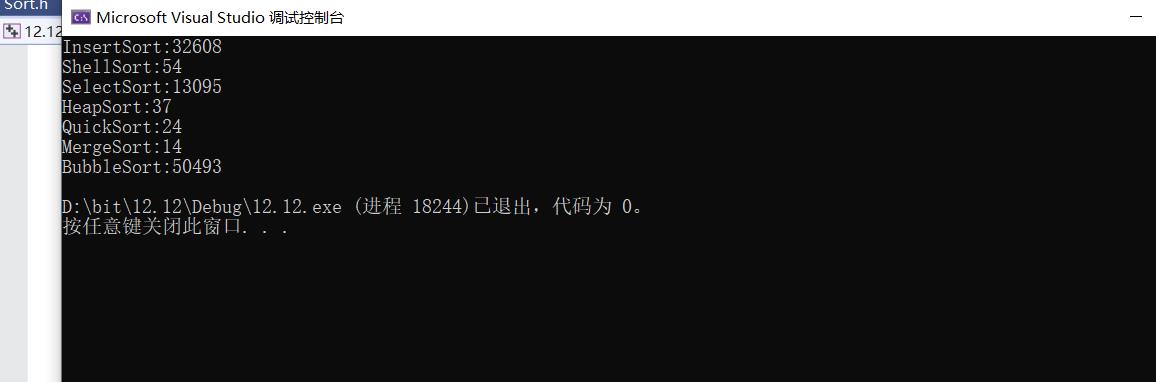
我输入的十万个数字进行排序,得到的结果是最优的是归并排序,最差的是冒泡排序。
注意这里的排序算法比较的均为比较排序算法,在算法设计与分析专栏中分治法那一篇文章已经证明了:在比较排序算法中时间复杂度最低为O(nlgn)。
而计数排序的复杂度可以达到O(n),但也有它的缺点和使用条件。
下面来详细分析这几个算法。
以从小到大排序为例
直接插入排序
排序方式
将每次待排序的数据插入之前已经排序好的数据中。
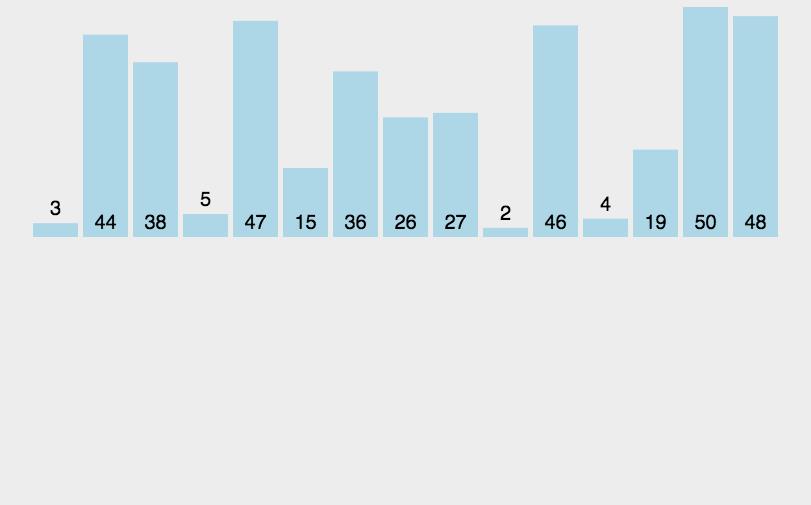
设计思路
1.首先使用for循环语句,得到待排序的数据。
2.将待排序数据与前面已经排序好的数据依次向前比较,若待排序的数据较小,则两者交换位置,否则退出循环。
代码实现
void InsertSort(int* a, int n)
assert(a);
int i;
for (i = 0; i < n - 1; i++)//外层循环次数
int end = i;
while (end >= 0)
int x = a[end + 1];//end+1记录要进行插入的元素
if (x < a[end])
Swap(&a[end+1], &a[end]);//将end与end+1进行比较
end--;
else
break;//否则退出循环
//内层循环的两个截止条件
希尔排序
排序方式
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序。
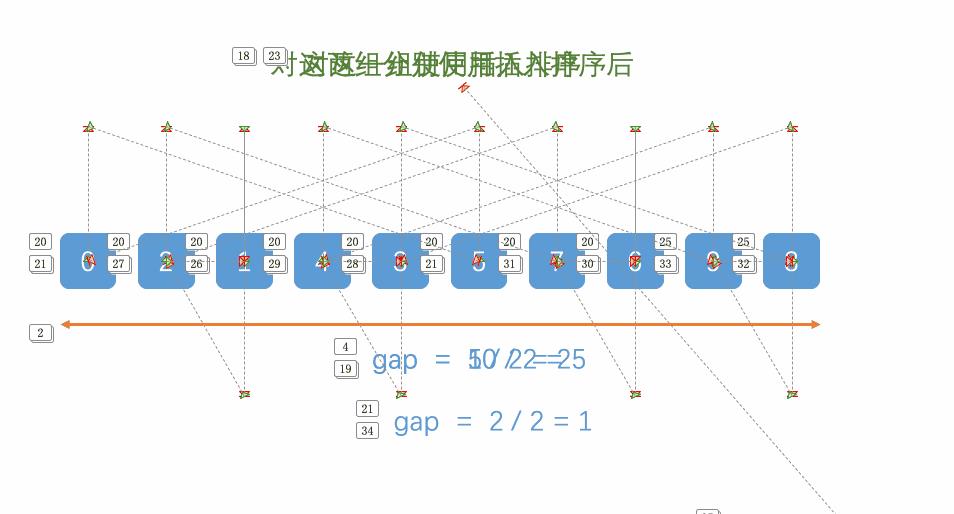
设计思路
1.一层循环控制gap的值从n开始到1为止的变化。每次n/2。
2.一层循环控制对于每一个gap的值,需要插入数据的个数。
3.一层循环找到待排序的数据。(每个待排序的数据之间相差gap)
4.将待排序的数据插入到已经排好序的序列中。
代码实现
void ShellSort(int* a, int n)
int gap = n;
while (gap >= 1)//gap的循环次数
gap = gap / 2;
int i,j;
for (i = 0; i < gap; i++)//外层循环次数
for (j = i; j < n - gap; j = j + gap)//内层循环次数
int end = j;
while (end >= 0)
if (a[end] > a[end + gap])
Swap(&a[end], &a[end + gap]);
end = end - gap;//与之相差gap距离的数字进行比较
else
break;
选择排序
排序方式
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
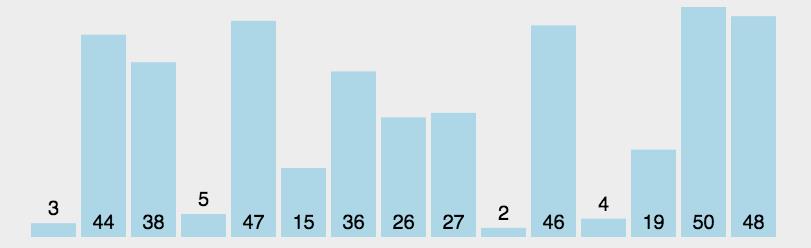
设计思路
1.定义首尾两个指针分别为begin,end
2.遍历从begin到end的数据,从中选择最小值与begin处的数据交换,最大值与end处的数据交换。
3.begin++,end–重复上述过程,直到begin>=end。
void SelectSort(int* a, int n)
int begin = 0;
int end = n - 1;
while (end >= begin)//定义循环次数
int maxi=a[end];
int mini= a[begin];
int i;
for (i = begin; i <= end; i++)//每次选择最大最小值
if (a[i] < mini)
mini = a[i];
Swap(&a[begin], &a[i]);//最小值放在数组首
if (a[i] > maxi)
maxi = a[i];
Swap(&a[end], &a[i]);//最大值放在数组尾
begin++;
end--;
堆排序
排序方式
利用堆这种数据结构所设计的一种排序算法。
设计思路
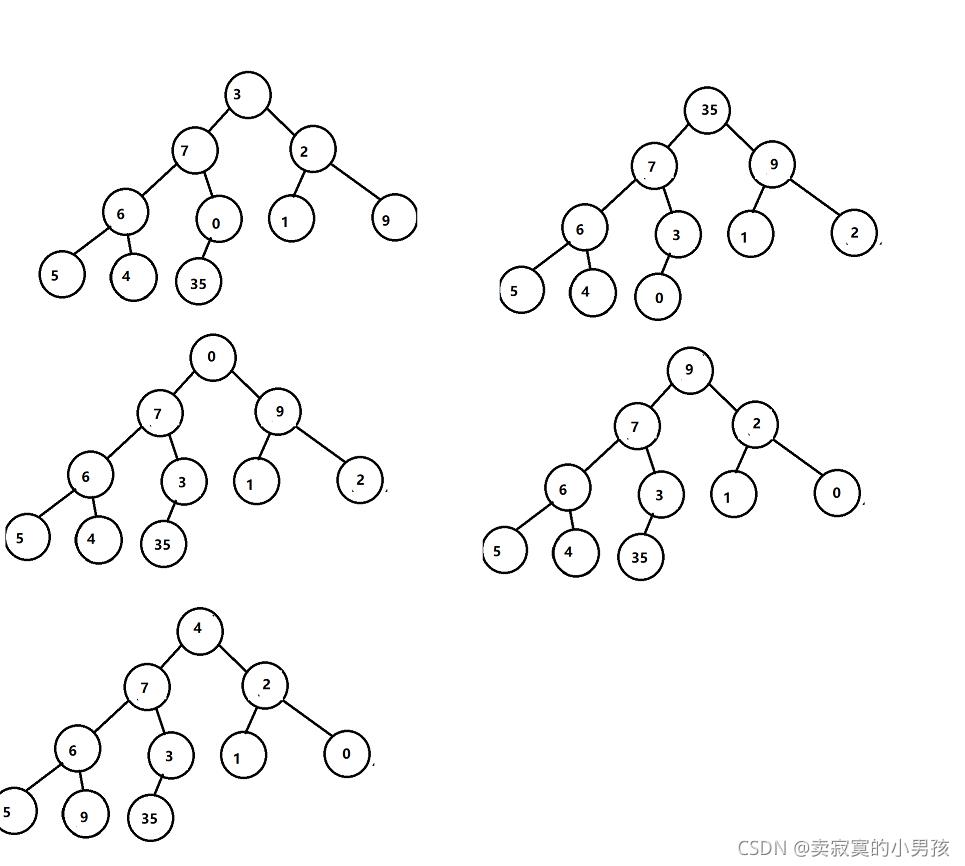
堆排序一共分为两步:
1.对所有有子节点或者子树的节点进行从左向右,从上向下进行向下调整。**向下调整的本质是找出一棵最小二叉树中节点的最大值。**所以最后调整之后建立了一个堆,堆顶点是这组数的最大值。
2.交换堆顶点与最后一个元素,在堆中对最后一个元素进行向下调整(不包含最后一个元素)。【这里和删除时一样的】,从而找出次大的数。
代码实现
void Adjustdown(int * a, int n, int parent) //向下调整算法
assert(a);
int child = 2 * parent + 1;
while (child < n)
if (child + 1 < n && a[child + 1] > a[child])
child++;
if (a[child] > a[parent])
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
else
break;
void HeapSort(int* a, int n)
int i;
for (i = (n - 2) / 2; i >= 0; i--)
Adjustdown(a, n, i);
for (int end = n - 1; end > 0; --end)
Swap(&a[end], &a[0]);
Adjustdown(a, end, 0);
冒泡排序
排序方法
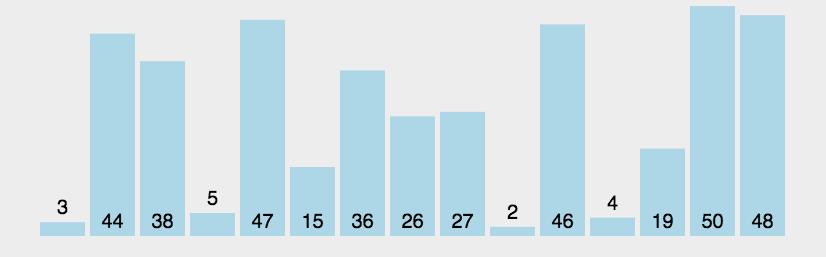
它重复地走访过要排序的元素列,依次比较两个相邻的元素,如果顺序(如从大到小、首字母从Z到A)错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换,也就是说该元素列已经排序完成。 这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端(升序或降序排列),就如同碳酸饮料中二氧化碳的气泡最终会上浮到顶端一样,故名“冒泡排序”。
设计思路
1.一层循环判断要执行几次操作(为n-1次)。
2.一层循环进行两两比较并交换。
当数组已经有序时,不需要再遍历许多次,可以定义flag变量来记录数组是否已经有序,有序则退出循环。
代码实现
void BubbleSort(int* a, int n)
int i, j;
for (i = 0; i < n - 1; i++)//循环n-1次,即找到n-1个最大的数
int flag = 1;
for (j = 0; j < n - i - 1; j++)//对相邻的两个数进行比较
if (a[j + 1] < a[j])
Swap(&a[j + 1], &a[j]);
flag = 0;
if (flag)
break;
快速排序
快速排序是最重要的排序算法,实现它有好多种方式。我们通常使用递归来实现它。
设计方法
1.选出一个大小适中的元素,放在数组首元素位置。
2.选择一种快速排序算法。并返回一个可递归数据。
3.进行递归。
选择大小适中的元素
为了保证时间复杂度,我们不能遍历所有的数据,然后找出中间值,所以我们取首,中,尾三个元素的中间值作为该大小适中的元素。
int GetMid(int* a, int left,int right)
int mid = (left+right) / 2;
if (a[left] > a[right])
if (a[left] < a[mid])
return left;
else if (a[right] > a[mid])
return right;
else
return mid;
else//left<right
if (a[right] < a[mid])
return right;
else if (a[mid] < a[left])
return left;
else
return mid;
选择快速排序算法
三种算法各有优劣,推荐选择第三种。
Partition1(Hoare版:初代)
设计方法
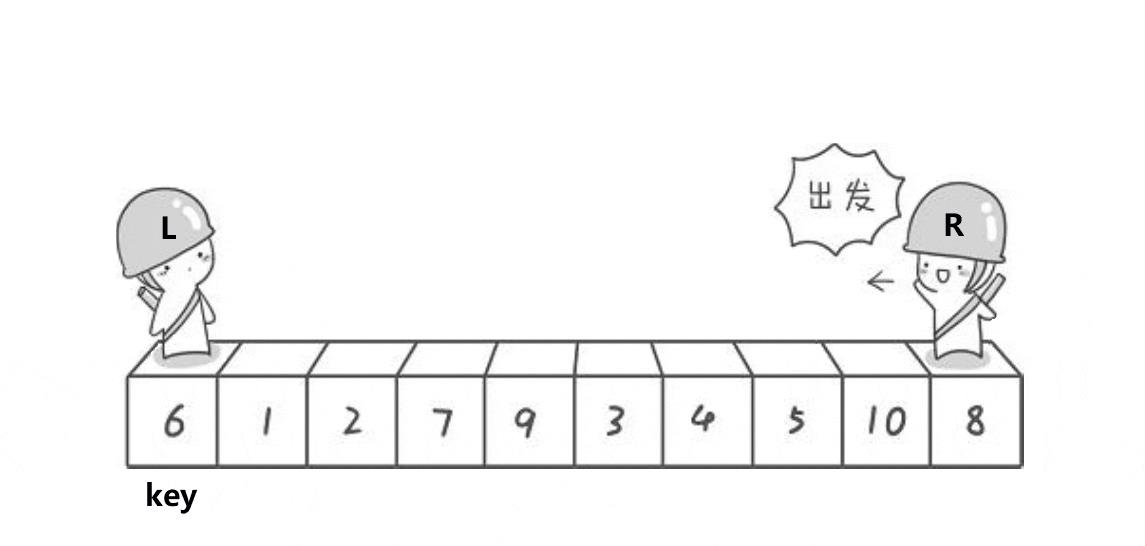
1.首先将选择的中间值放在数组首元素的位置。
2.定义两个指针left和right,分别从左向右,从右向左走。
3.当left遇到比中间值大的元素的时候停下来,当right遇到比中间值小的元素停下来。
4.交换left与right的元素。
5.当left>=right的时候停下来,将中间值(第一个元素)与left互换位置。
6.返回新的right和right。
本质上每一次递归都将中间值大的元素放在中间值的后面,比中间值小的元素放在中间值左边,即找到中间值在排好序的数组中的位置。
代码实现
int PartSort1(int* a, int left,int right)
int mini = GetMid(a,left,right);
Swap(&a[mini], &a[left]);//找到中间值并放在数组首元素的位置。
int keyi = left;
while (right > left)
while (left < right && a[right] >= a[keyi])
right--;
while (left < right && a[left] <= a[keyi])
left++;
Swap(&a[left], &a[right]);//交换两者的元素
Swap(&a[keyi], &a[left]);//交换中间值与左指针指向的元素
return left;
Partition2(挖坑法)
设计方法
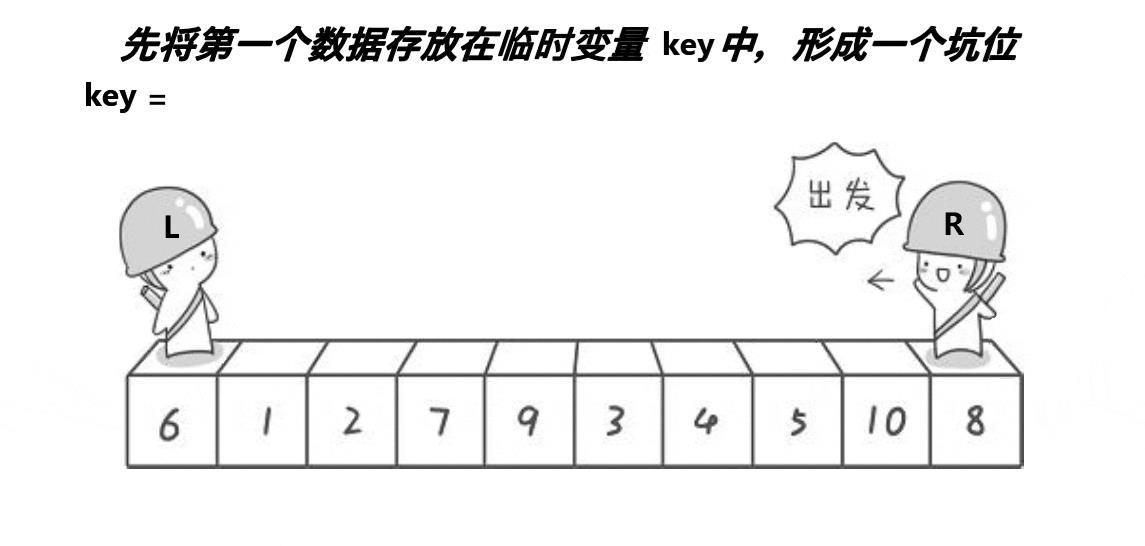
与初代版本相似,也是定义两个相向移动的指针。
1.将中间值与数组中第一个元素交换位置。此时认为第一个元素空缺即形成一个坑。
2.right指针向前移动,找到比中间值小的元素填入坑内,此时right所指向的位置形成了一个坑。
3.left指针向后移动,找到比中间值大的元素填入坑内,此时left所指向的位置形成了坑。
4.重复上述过程直到left>=right,此时讲中间值填入坑内。
5.返回新的right与left进行递归。
代码实现
int PartSort2(int* a, int left, int right)
int mini = GetMid(a, left, right);
Swap(&a[mini], &a[left]);
int key = a[left];
int pivot = left;//定义起始坑的位置
while (left < right)
while (left < right && a[right] >= key)
--right;
a[pivot] = a[right];
pivot = right;//将右指针的元素填入坑内,同时改变坑的位置
while (left < right && a[left] <= key)
++left;
a[pivot] = a[left];
pivot = left;
a[pivot] = key;
return pivot;//通过坑的位置寻找新的right和left
Partition3(前后指针法)

设计方法
与前两种方法的区别是,定义的两个指针是同向的。
1.将中间值放在数组首元素的位置。
2.定义指针prev和cur,prev为数组首元素的位置,cur为prev下一个元素的位置。
3.当cur位置的元素小于中间值,且prev+1!=cur时,prev++,然后交换prev与cur处的值。直到cur越界
4.交换中间值与prev处的值。
代码实现
int PartSort3(int* a, int left, int right)
int mini = GetMid(a, left, right);
Swap(&a[left], &a[mini]);
int prev = left;
int cur = prev + 1;//定义cur与prev的起始位置
while (cur <= right)
if (a[cur] < a[left] && ++prev != cur)//当cur处的值小于中间值时,prev++,注意&&的性质
Swap(&a[cur], &a[prev]);//交换cur与prev处的值
cur++;
Swap(&a[prev], &a[left]);
return prev;
进行递归
递归程序的设计模式是:首先写出递归终止条件,然后利用递归函数写最后一次递归,使用宏观思维。
void QuickSort(int* a, int left, int right)
if (left >= right)
return;//递归终止条件
int keyi = PartSort2(a, left, right);
//int keyi = PartSort3(a, left, right);