TensorFlow 线性支持向量机的使用

Posted 2020-11-18 x0216u

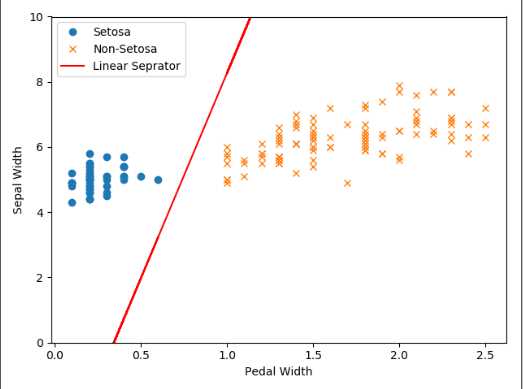
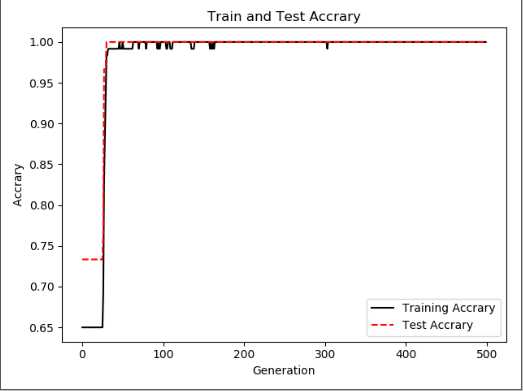
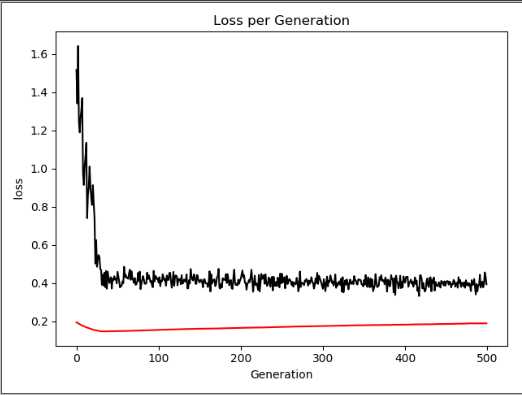
#在TensorFlow实现一个soft margin 支持向量机
#损失函数 惩罚项 使用L2范数
# 1/n*Σmax(0, y(Ax-b)) +Σ||A||^2
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from sklearn import  datasets

sess=tf.Session()
#加载鸢尾花集合
iris=datasets.load_iris()
#提取特征
x_vals=np.array([ [x[0],x[3] ]for x in iris.data])
#山鸢尾花为1 否则为-1
y_vals=np.array([  1 if y==0 else -1  for y in iris.target])

#分割训练集 测试集
train_indices=np.random.choice(len(x_vals),round(len(x_vals)*0.8),replace=False)
test_indices=list(set(range(len(x_vals)))-set(train_indices))
#数组分片操作 使得 x_vals必须要array类型
x_vals_train=x_vals[train_indices]
y_vals_trian=y_vals[train_indices]

x_vals_test=x_vals[test_indices]
y_vals_test=y_vals[test_indices]

#设置批量大小 希望用非常大的批量 因为小的批量会使 最大间隔线缓慢移动
batch_size=80

#设置变量 占位符
x_data=tf.placeholder(shape=[None,2],dtype=tf.float32)
y_target=tf.placeholder(shape=[None,1],dtype=tf.float32)

A=tf.Variable(tf.random_normal(shape=[2,1]))
b=tf.Variable(tf.random_normal(shape=[1,1]))

#输出 y=Ax-b
model_out=tf.subtract(tf.matmul(x_data,A),b)

#声明最大间隔损失函数。首先声明一个函数计算L2范数，接着增加间隔参数alpha
l2_norm=tf.reduce_sum(tf.square(A))
alpha=tf.constant([0.1])
l2=tf.multiply(alpha,l2_norm)
#分类器 该处y为真实值  1/n*Σmax(0, y(Ax-b)) +Σ||A||^2
classification_term=tf.reduce_mean(tf.maximum(0.,tf.subtract(1.,tf.multiply(y_target,model_out))))
loss=tf.add(classification_term,l2)

#增加预测函数 和 准确度函数
prediction=tf.sign(model_out)  #tf.sign ==-1,0,1
accuracy=tf.reduce_mean(tf.cast(tf.equal(prediction,y_target) ,tf.float32))
#梯度下降
my_opt=tf.train.GradientDescentOptimizer(0.01)
train_step=my_opt.minimize(loss)

#初始化上述变量
init=tf.global_variables_initializer()
sess.run(init)

#开始遍历迭代
loss_rec=[]
train_acc_rec=[]
test_acc_rec=[]
l2_rec=[]
for i in range(500):
    rand_index=np.random.choice(len(x_vals_train),size=batch_size)
    #shape(None,2)
    rand_x= x_vals_train[rand_index]
    rand_y= np.transpose([y_vals_trian[rand_index]])
    #运行
    sess.run(train_step,feed_dict={x_data:rand_x,y_target:rand_y})
    temp_loss =sess.run(loss,feed_dict={x_data:rand_x,y_target:rand_y})
    #添加记录
    loss_rec.append(temp_loss)
    #带入所有训练集 查看精确度
    train_acc_temp=sess.run(accuracy,feed_dict={x_data:x_vals_train,y_target:np.transpose([y_vals_trian])})
    train_acc_rec.append(train_acc_temp)
    # 带入所有测试集 查看精确度
    test_acc_temp=sess.run(accuracy,feed_dict={x_data:x_vals_test,y_target:np.transpose([y_vals_test])})
    test_acc_rec.append(test_acc_temp)
    l2_rec.append(sess.run(l2))
    #打印
    if (i+1)%100==0:
        print(‘Step:%d  A=%s ‘%(i,str(sess.run(A))))
        print(‘b=%s‘%str(sess.run(b)))
        print(‘Loss:%s‘% str(temp_loss))

#抽取系数 画图
[[a1],[a2]]=sess.run(A)
[[b]]=sess.run(b)
#a1x1+a2*x2-b=0 ==> x1=-a2*x2/a1 +  b/a1
slope=-a2/a1
y_intercept=b/a1
x1_vals=[ x[1] for x in x_vals]
#最优分割线 对应所有数据
best_fit=[]
for i in x1_vals:
    best_fit.append(slope*i+y_intercept)
#展示全部数据
setosa_x=[ s[1] for i,s in enumerate(x_vals) if y_vals[i] == 1]
setosa_y=[ s[0] for i,s in enumerate(x_vals) if y_vals[i] == 1]

not_setpsa_x=[ s[1] for i,s in enumerate(x_vals) if y_vals[i] == -1]
not_setpsa_y=[ s[0] for i,s in enumerate(x_vals) if y_vals[i] == -1]
plt.plot(setosa_x,setosa_y,‘o‘,label=‘Setosa‘)
plt.plot(not_setpsa_x,not_setpsa_y,‘x‘,label=‘Non-Setosa‘)
plt.plot(x1_vals,best_fit,‘r-‘,label=‘Linear Seprator‘)
plt.xlabel(‘Pedal Width‘)
plt.ylabel(‘Sepal Width‘)
plt.ylim([0,10])
plt.legend(loc=‘upper left‘)
plt.show()

plt.plot(train_acc_rec,‘k-‘,label=‘Training Accrary‘)
plt.plot(test_acc_rec,‘r--‘,label=‘Test Accrary‘)
plt.title(‘Train and Test Accrary‘)
plt.xlabel(‘Generation‘)
plt.ylabel(‘ Accrary ‘)
plt.legend(loc=‘lower right‘)
plt.show()


plt.plot(loss_rec,‘k-‘,label=‘Loss‘)
plt.title(‘Loss per Generation‘)
plt.xlabel(‘Generation‘)
plt.ylabel(‘ loss ‘)
plt.plot(l2_rec,‘r-‘,label=‘L2‘)
plt.show()