luogu_P2154 [SDOI2009]虔诚的墓主人

Posted 2021-05-07 coclhy

传送门：https://www.luogu.org/problem/P2154

先说说我犯的错误：

1. 眼瞎没看到100%的数据范围
2. 没有判断合法状态
3. 树状数组写挂了（对单点修，区间查理解脑残了）

看下面这个图

 

 

 

 

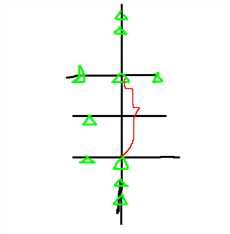
在红色区域内的墓地，它的上下的c(down,k)*c(up,k)是不变的，所以我们可以利用这个性质。

那我们怎么得到它的左右两边的组合数积呢?

我们发现左右的组合数对答案的贡献满足加法原理的。所以我们可以维护一个单点修改区间查询的树状数组来处理这个问题。

在每次扫到一颗树的时候就对树状数组进行维护更新的值为 当前的贡献-上一状态的贡献。

#include<bits/stdc++.h>
#define R register
typedef long long ll;
using namespace std;
const ll mod=2147483648LL;
int n,m,tot,cnt,X[110000],Y[110000],x_,y_,nx[110000],ny[110000],le[110000],down[110000],mx;
struct ddd{
    int x,y;
}p[110000];
inline bool com(ddd a,ddd b){
    if(a.x==b.x) return a.y<b.y;
    return a.x<b.x;
}
ll c[110000][13],szsz[110000],ans;
void add(int x,ll v){
    for(;x<=mx;x+=x&-x) szsz[x]=(szsz[x]+v+mod)%mod;
}
ll ask(int x){
    ll to=0;
    for(;x;x-=x&-x) to=(to+szsz[x]+mod)%mod;
    return to;
}
int main (){
    scanf("%d%d%d",&n,&m,&tot);
    for(R int i=1;i<=tot;i++){
        scanf("%d%d",&p[i].x,&p[i].y);
        X[++x_]=p[i].x;Y[++y_]=p[i].y;
    }
    scanf("%d",&cnt);
    sort(X+1,X+1+x_);
    sort(Y+1,Y+1+y_);
    x_=unique(X+1,X+1+x_)-X-1;
    y_=unique(Y+1,Y+1+y_)-Y-1;
    for(R int i=1;i<=tot;i++){
        p[i].x=lower_bound(X+1,X+1+x_,p[i].x)-X;
        p[i].y=lower_bound(Y+1,Y+1+y_,p[i].y)-Y;
        nx[p[i].x]++;
        ny[p[i].y]++;
        mx=max(mx,p[i].y);
    }
    sort(p+1,p+1+tot,com);
    for(R int i=0;i<=tot;i++) c[i][0]=1;
    for(R int i=1;i<=tot;i++){
        for(R int j=1;j<=cnt;j++){
            c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
        }
    }
    for(R int i=1;i<=tot;i++){
        le[p[i].y]++;
        down[p[i].x]++;
        add(p[i].y,(c[le[p[i].y]][cnt]*c[ny[p[i].y]-le[p[i].y]][cnt]-c[le[p[i].y]-1][cnt]*c[ny[p[i].y]-le[p[i].y]+1][cnt]+mod)%mod);
        if(p[i].x!=p[i+1].x) continue;
        if(c[down[p[i].x]][cnt]*c[nx[p[i].x]-down[p[i].x]][cnt]) ans=(ans+(c[down[p[i].x]][cnt]*c[nx[p[i].x]-down[p[i].x]][cnt]%mod)*((ask(p[i+1].y-1)-ask(p[i].y)+mod)%mod))%mod;
    }
    printf("%lld",(ans+mod)%mod);
    return 0;
}

View Code