可持久化数据结构

Posted 2021-05-07 equinox-flower

可持久化数据结构

可持久化线段树

据说这个东西是(hjt)发明的(不是国家领导人

由于上句所述原因,又称主席树.
这个东西有啥用呢?
支持历史版本的查询.
这有啥用?出题考你
实现历史版本查询的一个朴素想法是:
对于每一个版本都建一棵线段树,开桶记录根节点,每次对应查询即可.
这样的正确性是显然的,时间复杂度也是对的.
那为什么还要可持久化线段树呢?
因为朴素的做法的空间复杂度(Theta(4n imes m))或者(Theta(2n imes m)).
其中(n)是数据规模,(m)是版本个数,(2n)和(4n)取决于线段树写法.
那么,可持久化线段树的时空复杂度如何呢?时间复杂度当然不会更劣.
空间复杂度大概在(Theta(2n+m imes log_2{n}))或(Theta(4n+m imes log_2{n})).各字母含义与上述相同.
和上面相比相当的优秀.为什么呢?
因为我们对于每一个版本都只需要新建至多(log_2{n})个节点.
上图:

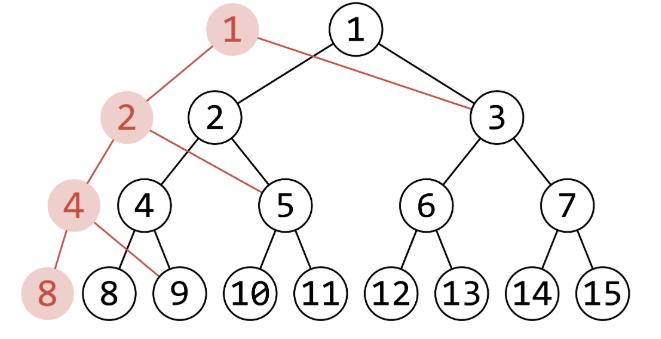
一棵构建好的主席树也就差不多这样.
它避免了重建整棵树,而是选择把原树中相对于新版本没有改变的节点加以利用,从而达到了节省空间的目的.
然后你可能会说这不是一棵树,因为它每个节点不只有一个父亲(看起来
但其实不是,因为主席树其实是由若干棵部分空间共享的线段树组成的,图上多出来的父亲关系其实是另一棵线段树的结构,而不属于本棵线段树,因此你在访问的时候实际访问到的是一棵正常的线段树.
那么它这样的结构如何访问呢?
根节点还是开桶记录,(如果桶开不下说明这题显然不可用主席树做
这个时候,其实我们会发现,这一组线段树其实是一个前缀和的形式.
所以它遵循前缀和的规则.
其他的地方其实和普通线段树一般无二.
经典例题:静态区间第k大
首先肯定要离散化+权值线段树的.
这里我们的主席树是可持久化权值线段树.
每一棵树表示一个前缀的权值信息.
查询的时候把对应区间的两棵线段树相减再去二分地找即可.

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <string>
#include <vector>
#include <queue>
#include <cmath>
#include <ctime>
#include <map>
#include <set>
#define MEM(x,y) memset ( x , y , sizeof ( x ) )
#define rep(i,a,b) for (int i = (a) ; i <= (b) ; ++ i)
#define per(i,a,b) for (int i = (a) ; i >= (b) ; -- i)
#define pii pair < int , int >
#define one first
#define two second
#define rint read<int>
#define int long long
#define pb push_back
#define db double

using std::queue ;
using std::set ;
using std::pair ;
using std::max ;
using std::min ;
using std::priority_queue ;
using std::vector ;
using std::swap ;
using std::sort ;
using std::unique ;
using std::greater ;

template < class T >
    inline T read () {
        T x = 0 , f = 1 ; char ch = getchar () ;
        while ( ch < '0' || ch > '9' ) {
            if ( ch == '-' ) f = - 1 ;
            ch = getchar () ;
        }
       while ( ch >= '0' && ch <= '9' ) {
            x = ( x << 3 ) + ( x << 1 ) + ( ch - 48 ) ;
            ch = getchar () ;
       }
       return f * x ;
}

const int N = 2e5 + 100 ;

int n , m , v[N] , w[N] ;

class Chairman {
    #define mid ( ( l + r ) >> 1 )
    private :
        struct seg { int lson , rson , data ; } t[N*20] ;
    private : int cnt ;
    public : int rt[N] ;
    public :
        inline void initial () { cnt = 0 ; return ; }
    private :
        inline void pushup (int rt) { t[rt].data = t[t[rt].lson].data + t[t[rt].rson].data ; }
    public :
        inline void insert (int & rt , int l , int r , int key) {
            t[++cnt] = t[rt] ; rt = cnt ;
            if ( l == r ) { ++ t[rt].data ; return ; }
            if ( key <= mid ) insert ( t[rt].lson , l , mid , key ) ;
            else insert ( t[rt].rson , mid + 1 , r , key ) ;
            pushup ( rt ) ; return ;
        }
    public :
        inline int query (int u , int v , int l , int r , int key) {
            if ( l == r ) return l ;
            int T = t[t[v].lson].data - t[t[u].lson].data ;
            if ( key <= T ) return query ( t[u].lson , t[v].lson , l , mid , key ) ;
            else return query ( t[u].rson , t[v].rson , mid + 1 , r , key - T ) ;
        }
    #undef mid
} T ;

signed main (int argc , char * argv[]) {
    n = rint () ; m = rint () ; T.initial () ;
    rep ( i , 1 , n ) w[i] = v[i] = rint () ;
    sort ( w + 1 , w + n + 1 ) ; w[0] = unique ( w + 1 , w + n + 1 ) - w - 1 ;
    rep ( i , 1 , n ) v[i] = std::lower_bound ( w + 1 , w + w[0] + 1 , v[i] ) - w ;
    T.rt[0] = 0 ; rep ( i , 1 , n ) T.rt[i] = T.rt[i-1] , T.insert ( T.rt[i] , 1 , w[0] , v[i] ) ;
    rep ( i , 1 , m ) {
        int l = rint () , r = rint () , k = rint () ;
        printf ("%lld
" , w[T.query ( T.rt[l-1] , T.rt[r] , 1 , w[0] , k )] ) ;
    }
    system ("pause") ; return 0 ;
}

可持久化数组

可持久化数组是可持久化并查集的基础,如果要学习可持久化并查集,该数据结构是绕不过去的门槛.
可持久化数组的经典操作在下面的模板题中已经给出:
模板:可持久化数组
这里的版本就比较明显了.
而且这显然可以使用主席树去维护.
直接按照题意用主席树模拟即可.
只需要单点修改,单点查询.
(注:可持久化数组并非只能用可持久化线段树实现,其他数据结构例如可持久化(Treap)也是可以是实现的,据说还有一个不依赖于其他数据结构的真·可持久化数组写法,但笔者并不会.)

#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <string>
#include <vector>
#include <queue>
#include <cmath>
#include <ctime>
#include <map>
#include <set>
#define MEM(x,y) memset ( x , y , sizeof ( x ) )
#define rep(i,a,b) for (int i = (a) ; i <= (b) ; ++ i)
#define per(i,a,b) for (int i = (a) ; i >= (b) ; -- i)
#define pii pair < int , int >
#define one first
#define two second
#define rint read<int>
#define int long long
#define pb push_back
#define db double

using std::queue ;
using std::set ;
using std::pair ;
using std::max ;
using std::min ;
using std::priority_queue ;
using std::vector ;
using std::swap ;
using std::sort ;
using std::unique ;
using std::greater ;

template < class T >
    inline T read () {
        T x = 0 , f = 1 ; char ch = getchar () ;
        while ( ch < '0' || ch > '9' ) {
            if ( ch == '-' ) f = - 1 ;
            ch = getchar () ;
        }
       while ( ch >= '0' && ch <= '9' ) {
            x = ( x << 3 ) + ( x << 1 ) + ( ch - 48 ) ;
            ch = getchar () ;
       }
       return f * x ;
}

const int N = 1e6 + 100 ;

int n , m , v[N] , now ;

class Chairman {
    #define mid ( ( l + r ) >> 1 )
    public : int rt[N] ;
    private : int cnt ;
    private : struct seg { int lson , rson , data ; } t[N*20] ;
    public : inline void initial () { cnt = 1 ; return ; }
    public :
        inline void build (int rt , int l , int r) {
            if ( l == r ) { t[rt].data = v[l] ; return ; }
            t[rt].lson = ++ cnt ; build ( t[rt].lson , l , mid ) ;
            t[rt].rson = ++ cnt ; build ( t[rt].rson , mid + 1 , r ) ;
            return ;
        }
    public :
        inline void update (int & rt , int l , int r , int pos , int key) {
            t[++cnt] = t[rt] ; rt = cnt ;
            if ( l == r ) { t[rt].data = key ; return ; }
            if ( pos <= mid ) update ( t[rt].lson , l , mid , pos , key ) ;
            else update ( t[rt].rson , mid + 1 , r , pos , key ) ;
            return ;
        }
    public :
        inline int query (int rt , int l , int r , int pos) {
            if ( l == r ) return t[rt].data ;
            if ( pos <= mid ) return query ( t[rt].lson , l , mid , pos ) ;
            else return query ( t[rt].rson , mid + 1 , r , pos ) ;
        }
    #undef mid
} T ;

signed main (int argc , char * argv[]) {
    n = rint () ; m = rint () ; T.initial () ;
    rep ( i , 1 , n ) v[i] = rint () ;
    T.build ( 1 , 1 , n ) ; T.rt[0] = 1 ;
    while ( m -- ) {
        int k = rint () , opt = rint () , x = rint () ;
        if ( opt == 1 ) {
            int y = rint () ; int tmp = T.rt[k] ;
            T.update ( tmp , 1 , n , x , y ) ;
            T.rt[++now] = tmp ;
        }
        if ( opt == 2 ) {
            T.rt[++now] = T.rt[k] ;
            printf ("%lld
" , T.query ( T.rt[k] , 1 , n , x ) ) ;
        }
    }
    system ("pause") ; return 0 ;
}