数据分析-评估指标(F1score和ROC曲线)

Posted

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据分析-评估指标(F1score和ROC曲线)相关的知识，希望对你有一定的参考价值。

参考技术A

这里我介绍数据分析的两个评估指标， F1 score 跟 ROC曲线 ，在介绍F1 score跟ROC曲线之前，我们要先了解以下概念：

什么是混淆矩阵，我们来看下图：

注意，在上图中，蓝点是阳性，红点是阴性。
一般从医学角度说，阳性（positive），代表有病或者有病毒，阴性（negative），代表正常。

我们来上述模型有多少真阳性、真阴性、假阳性、假阴性？

上图，这就是混淆矩阵。

下面我们来学习衡量模型性能的一种方式，准确率。
准确率是什么？我们继续引用上面的图片

准确率就是在图表所有数据里，正确分类的点有多少，就是正确分类的点和总点数的比例；数学公式就是准确率=正确分类的点/总点数。
上图中，正确分类=真阳性（6）+ 真阴性（5）= 11；总点数为14

上图的准确率=11/14=0.7857

在了解精准率之前，我们来看看下面的医学预测图：

精准率的定义就是在所有预测阳性的点里有多少是真阳性？换种说法就是在所有诊断为病人中，有多少是真正的病人？

在图中可以看出，精准率都在Diagnosed sick 这一列

这一列都是诊断为阳性的数据。真阳性的数量是1000，所有阳性的数量是1000+800=1800；

所以精准率(precision) = 1000/1800=55.6%

那下图的精准率呢？

精准率是在所有预测所有诊断为病人中，有多少是真正的病人，召回率是在所有真正病人中，有多少是成功诊断为病人。召回率这里所有真正的病人是真阳性（true positive）跟 假阴性（false negative）的和，因为假阴性（false negative）是是将有病的检查为没病也是病人。

所以召回率是统计sick 这一行

这一列都是诊断为阳性的数据。真阳性的数量是1000，所有病人的数量是是真阳性（true positive）跟 假阴性（false negative）的和，1000+200=1200；

所以召回率(recall) = 1000/1200=83.3%

那下图的召回率呢？

在上面我们已经学习了精准率(precision) 跟召回率(recall) 了，从上面我们知道医疗模型的精准率(precision) 55.6%，召回率(recall) 是 83.3%，这是个高召回率模型（如果精准率(precision) 高，召回率(recall) 低那就是高精准率模型）。

现在问题是，这里有两个指标，我们每次判断模型是高精准率模型还是高召回率模型都要使用这个两个指标来判断么，这样很不方便，有没有一个指标就可以直接判断出来，这个指标就是F1 score。

问题是我们怎么把这个两个分数合并在一起呢？你能想出方法来么，有个简单的方式就是取精准率(precision) 跟召回率(recall) 这个两个数的平均值，我们可以得到平均值(55.6%+83.3%)/2=69.45%，这是一个可以接受的指标，但是取平均值没有给我们提供更多的信息，我们来在一个极端的例子来检验平均值；

比如以信用卡欺诈检测为例，图中我们有很多正常和欺诈的交易

从图中可以算出，欺诈交易比例=472/(472+284335)=0.16%。

我们使用混淆矩阵来分析它，上面《全部交易都是欺诈交易》极端模型有真阳性（472）、真阴性（0）、假阳性（284335）、假阴性（0）
该模型的精准率(precision)是就是所有我们判断为欺诈行为里面有多少真正的欺诈交易，因为我们定义所有交易都是欺诈交易，所以精准率(precision)=472/(472+284335)=0.16%，召回率(recall) 就是真正的欺诈交易里，有多少我们成功判断为欺诈行为，所以召回率(recall)=472/472=100%。

如果是取平均值作为指标来判断的话，这里平均值就是50.08%；
在这个极端模型里面使用50.08%来判断欺诈交易分数还是太高了，我们应该给一个更低的分数，甚至是零分，所以取平均值作为指标不是最好的方法。

原则上如果精准率(precision)和召回率(recall)有一个值非常低，即使另一个指标非常高，我们也想给它一个低分，这里有一个解决方案，就是 调和平均值 。
它的工作原理如下：
假设我们有两个值：x，y，x比y小，中间的值就是平均值，比平均值小的就是调和平均值，调和平均值总是小于平均值，如果两个x和y值相等，调和平均值就是平均值。调和平均值比较接近较小的数值，而不是较大的数值。所以调和平均值总是接近精准率(precision)和召回率(recall)之中的最小值。

F1 得分练习
接下来，请记住 F1 得分的公式为：

注意，在 F-β 得分公式中，如果设β=0, 则

因此， β 的最低值为 0，这时候就得出高精准率。

注意，如果 N 非常大，则

随着 Nˉ2 变成无穷大，可以看出，1/1+Nˉ2 变成 0，并且Nˉ2/1+Nˉ2会变成 1，
因此，如果取极限值，则

因此，得出结论：β 的界限在 0 和 无穷大∞ 之间。

练习：
在下面的三个模型中，哪个的 F-β 得分应该是 2、1 和 0.5？每个模型的相应的得分应该是多少？

答案是宇宙飞船的β 值是2，手机通知是1，免费样品是0.5

解答： 对于宇宙飞船，我们不允许出现任何故障零件，可以检查本身能正常运转的零件。因此，这是一个高召回率模型，因此 β = 2。
对于通知模型，因为是免费发送给客户，如果向更多的用户发送邮件也无害。但是也不能太过了，因为可能会惹怒用户。我们还希望找到尽可能多感兴趣的用户。因此，这个模型应该具有合适的精度和合适的召回率。β = 1 应该可行。
对于免费样品模型，因为寄送样品需要成本，我们不希望向不感兴趣的用户寄送样品。因此是个高精度模型。β = 0.5 应该可行。

在了解ROC曲线是怎么形成的，ROC将伪阳性率（FPR）定义为 X 轴，真阳性率（TPR）定义为 Y 轴，根据多种划分方式，得到一组（x，y）轴数据来组成的曲线， 我们来看下图，假设红蓝点都在一条线上，我们怎么划分它们呢，可以有很多中划分，比如图中红色划线的5种划分方式；

现在我们来说一下它们的伪阳性率（FPR）跟真阳性率（TPR）是多少？
首先我们来看最左边的划线，算一下（x，y）的值是多少
伪阳性率（flase positive rate）= false positives/ all negatives = 7/7=1；
真阳性率（true positive rate）= true positives/ all positives = 7/7=1；

然后我们来看最右边的划线，算一下（x，y）的值是多少
伪阳性率（flase positive rate）= false positives/ all negatives = 0/7=0；
真阳性率（true positive rate）= true positives/ all positives = 0/7=0；

从中可以看出，不管数据极端怎么变好，计算的坐标值都是在(0, 0) 到 (1,1) 的之间；

我们来看一下中间那条线的划分的（x，y）的值是多少
伪阳性率（flase positive rate）= false positives/ all negatives = 2/7=0。286；
真阳性率（true positive rate）= true positives/ all positives = 6/7=0.857；

你们可以移动该线条，计算不同的（x，y）的值，这里我就不一一计算了，计算出来的（x，y）数组，就可以画出ROC曲线。

从图中数据，我们可以计算ROC曲线的面积大概是area = 0.8；
不用的模型画出的ROC曲线不同，大概有下图的三种不同模型的ROC曲线；

第一种是随机划分的模型，第二种是比较好的划分模型，第三种是完美划分模型，随机划分的模型ROC曲线面积大概接近0.5，比较好的划分模型ROC曲线面积大概接近0.8，完美划分模型ROC曲线面积大概接近1，总的来说，ROC曲线面积越来越接近1，模型就越好。

机器学习中的性能指标：精度召回率，PR曲线，ROC曲线和AUC，及示例代码

机器学习中的性能指标：精度、召回率、PR曲线，ROC曲线和AUC

精度、召回率

基本概念

可以通过下图来帮助理解

预测为正/阳性预测为负/阴性指标
真值为正/阳性True Positive(TP)False Negative(FN) R e c a l l = T P T P + F N Recall = \\fracTPTP+FN Recall=TP+FNTP​
真值为负/阴性False Positive(FP)True Negative(TN) S p e c i f i c i t y = T N T N + F P Specificity=\\fracTNTN+FP Specificity=TN+FPTN​
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy= \\frac TP +TNTP+TN+FP+FN Accuracy=TP+TN+FP+FNTP+TN​ P r e c i s i o n = T P ( T P + F P ) Precision=\\fracTP(TP+FP) Precision=(TP+FP)TP​ F 1 S c o r e = 2 ∗ R e c a l l ∗ P r e c i s i o n R e c a l l + P r e c i s i o n F1 Score=\\frac2*Recall *PrecisionRecall+Precision F1Score=Recall+Precision2∗Recall∗Precision​

  • 精度 （ P r e c i s i o n ） （Precision） （Precision）:预测为阳性样本的准确程度。在信息检索领域也叫查准率。换句话理解：判定为阳性的正确个数除以所有判定为阳性的总素。

  • 召回率 ( R e c a l l ) (Recall) (Recall):也称作敏感度（sensitivity），全部阳性样本中被预测为阳性的比例。在信息检索领域也称作查全率。

    其中精度和召回率同时越高，说明模型性能越好。但精度和召回率在某些情况下是相互矛盾。例如：
    阳性/阴性=50/50，模型只识别出一个为阳性，其余被识别为阴性。此时precision=1/(1+0)=100%, recall=1/(1+49)=2%.

F-Score

通过加权平均综合precision和recall，可以得到F-Score：
F S c o r e = ( 1 + a 2 ) ∗ R e c a l l ∗ P r e c i s i o n a 2 ∗ P r e c i s i o n + R e c a l l F Score=\\frac(1+a^2)*Recall *Precisiona^2*Precision+Recall FScore=a2∗Precision+Recall(1+a2)∗Recall∗Precision​
设置 a = 1 a=1 a=1，可以得到F1-Score:
F 1 − s c o r e = 2 ∗ R e c a l l ∗ P r e c i s i o n R e c a l l + P r e c i s i o n F1-score=\\frac2*Recall *PrecisionRecall+Precision F1−score=Recall+Precision2∗Recall∗Precision​

度量曲线

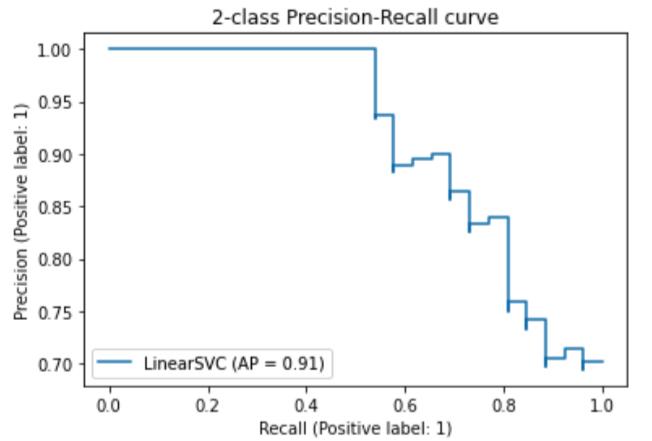
PR曲线

PR曲线(Precision-Recall Curve):

  • 横轴：召回率；
  • 纵轴：精度。

理想性能是右上角（1，1）处。PR曲线越往右上凸，说明模型性能越好。

PR曲线绘制方法：

  • 根据模型的预测数值，对样本进行从高到低排序，排在前面的样本是正例的可能性更高。
  • 按此顺序逐个样本作为正例进行预测（或设置阈值截断正例和负例），则每次可以计算一个召回率和精度。
  • 将这些值连成（拟合）一条曲线。

使用scikit-learn官方代码示例：
使用鸢尾花数据集来绘制PR曲线。

from sklearn.metrics import PrecisionRecallDisplay
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

X, y = load_iris(return_X_y=True)

# Add noisy features
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.concatenate([X, random_state.randn(n_samples, 200 * n_features)], axis=1)

# Limit to the two first classes, and split into training and test
X_train, X_test, y_train, y_test = train_test_split(
    X[y < 2], y[y < 2], test_size=0.5, random_state=random_state
)
classifier = make_pipeline(StandardScaler(), LinearSVC(random_state=random_state))
classifier.fit(X_train, y_train)
display = PrecisionRecallDisplay.from_estimator(
    classifier, X_test, y_test, name="LinearSVC"
)
_ = display.ax_.set_title("2-class Precision-Recall curve")

ROC曲线

ROC曲线(Receiver-operating-characteristic curve):

  • 横轴：False Positive rate(FPR)，度量所有阴性样本中被错误识别为阳性的比率。 F P R = 1 − S p e c i f i c i t y FPR=1-Specificity FPR=1−Specificity。
    F P R = F P F P + T N FPR =\\fracFPFP+TN FPR=FP+TNFP​
  • 纵轴：True positive rate(TPR),即recall。度量所有阳性样本被识别为阳性的比例。

理想性能在左上角(0,1)处。ROC曲线越往左上凸，说明模型性能越好。对角线为随机识别的ROC曲线。绘制方法与PR曲线相似。

PR曲线和ROC曲线的比较

  • ROC曲线：对于各类别之间样本分布比例不敏感，因为FPR和TPR各自只跟真值为负或真值为正的样本相关。
  • PR曲线：对于各类别样本分布比例敏感，因为precision同时和真值正负的样本都相关。

AUC

曲线下方面积（Area under the Curve, AUC）：将曲线度量所表达的信息浓缩到一个标量表达。

  • A U C = 1 AUC=1 AUC=1，是完美分类起
  • 0.5 < A U C < 1 0.5<AUC<1 0.5<AUC<1:优于随机猜测。模型妥善设定阈值，能有预测价值
  • A U C = 0.5 AUC=0.5 AUC=0.5:跟随机猜测一样，模型没有预测价值
  • A U C < 0.5 AUC<0.5 AUC<0.5：比随机猜想还差。

使用scikit-learn官方示例代码

import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle

from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from sklearn.metrics import roc_auc_score

# Import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target

# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]

# Add noisy features to make the problem harder
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]

# shuffle and split training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)

# Learn to predict each class against the other
classifier = OneVsRestClassifier(
    svm.SVC(kernel="linear", probability=True, random_state=random_state)
)
y_score = classifier.fit(X_train, y_train).decision_function(X_test)

# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

plt.figure(dpi=100)
lw = 2
plt.plot(
    fpr[2],
    tpr[2],
    color="darkorange",
    lw=lw,
    label="ROC curve (area = %0.2f)" % roc_auc[2],
)
plt.plot([0, 1], [0, 1], color="navy", lw=lw, linestyle="--")
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("Receiv
以上是关于数据分析-评估指标(F1score和ROC曲线)的主要内容，如果未能解决你的问题，请参考以下文章
 

 机器学习模型评估选择与验证


 ROC vs. PRC


 一文详解人工智能分类方面的KPI评价标准：混淆矩阵TPFPFNTNP-R曲线图ROC曲线图


 一文详解人工智能分类方面的KPI评价标准：混淆矩阵TPFPFNTNP-R曲线图ROC曲线图


 一文详解人工智能分类方面的KPI评价标准：混淆矩阵TPFPFNTNP-R曲线图ROC曲线图


 精确率与召回率，RoC曲线与PR曲线