集成学习lgb库调参的粒子群方法
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了集成学习lgb库调参的粒子群方法相关的知识,希望对你有一定的参考价值。
粒子群算法是模拟鸟群蜂群的觅食行为的一种算法。基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。试着想一下一群鸟在寻找食物,在这个区域中只有一只虫子,所有的鸟都不知道食物在哪。但是它们知道自己的当前位置距离食物有多远,同时它们知道离食物最近的鸟的位置。想一下这时候会发生什么?
鸟A:哈哈哈原来虫子离我最近!
鸟B,C,D:我得赶紧往 A 那里过去看看!
同时各只鸟在位置不停变化时候离食物的距离也不断变化,所以一定有过离食物最近的位置,这也是它们的一个参考。鸟某某:我刚刚的位置好像靠近了食物,我得往那里靠近!
公式请自行百度 知乎
具体代码流程如下: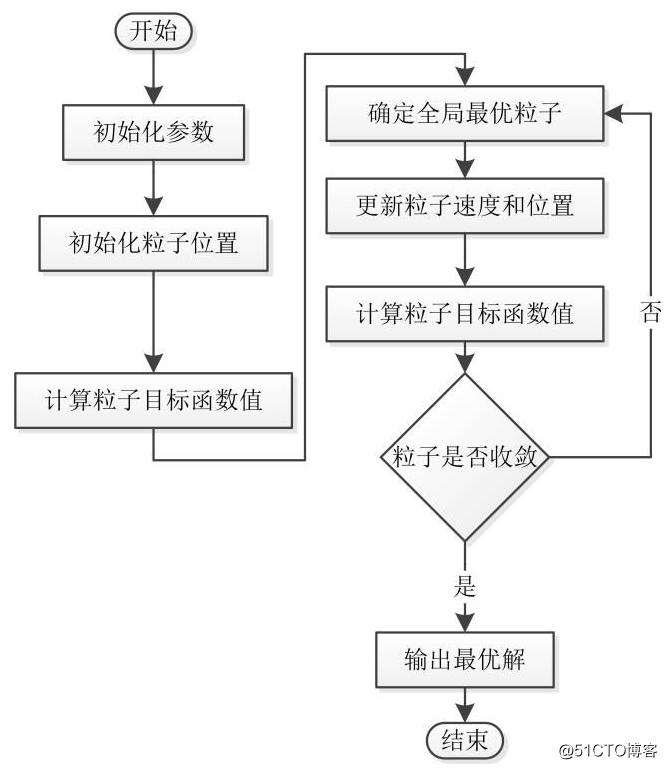
本文主要描述如何用粒子群方法搜索到一个适合lgb的参数
先要定一个损失函数:
def gini_coef(wealths):
cum_wealths = np.cumsum(sorted(np.append(wealths, 0)))
sum_wealths = cum_wealths[-1]
xarray = np.array(range(0, len(cum_wealths))) / np.float(len(cum_wealths)-1)
yarray = cum_wealths / sum_wealths
B = np.trapz(yarray, x=xarray)
A = 0.5 - B
return A / (A+B)当然也可以传入训练数据的标签值 和预测值做协方差 这里采用基尼系数作为损失函数
定义一个评估函数:用于评估该参数版本的效果如何:
def evaluate(train1 , feature_use,parent):
np.set_printoptions(suppress=True)
print("*************************************")
print(parent)
model_lgb = lgb.LGBMRegressor(objective=‘regression‘,
min_sum_hessian_in_leaf=parent[0],
learning_rate=parent[1],
bagging_fraction=parent[2],
feature_fraction=parent[3],
num_leaves=int(parent[4]),
n_estimators=int(parent[5]),
max_bin=int(parent[6]),
bagging_freq=int(parent[7]),
feature_fraction_seed=int(parent[8]),
min_data_in_leaf=int(parent[9]),
is_unbalance = True
)
targetme = train1[‘target‘]
X_train, X_test, y_train, y_test = train_test_split(train1[feature_use] , targetme, test_size=0.5)
model_lgb.fit(X_train.fillna(-1), y_train)
y_pred = model_lgb.predict(X_test.fillna(-1))
return gini_coef(y_pred)参数初始化代码:
## 参数初始化
# 粒子群算法中的两个参数
c1 = 1.49445
c2 = 1.49445
maxgen= 50 # 进化次数
sizepop= 100 # 种群规模
Vmax1=0.1
Vmin1=-0.1
## 产生初始粒子和速度
pop=[]
V = []
fitness =[]
for i in range(sizepop):
# 随机产生一个种群
temp_pop =[]
temp_v = []
min_sum_hessian_in_leaf = random.random()
temp_pop.append(min_sum_hessian_in_leaf)
temp_v.append(random.random())
learning_rate = random.uniform(0.001,0.2)
temp_pop.append(learning_rate)
temp_v.append(random.random())
bagging_fraction = random.uniform(0.5,1)
temp_pop.append(bagging_fraction)
temp_v.append(random.random())
feature_fraction = random.uniform(0.3,1)
temp_pop.append(feature_fraction)
temp_v.append(random.random())
num_leaves = random.randint(3,100)
temp_pop.append(num_leaves)
temp_v.append(random.randint(-3,3))
n_estimators = random.randint(800,1200)
temp_pop.append(n_estimators)
temp_v.append(random.randint(-3,3))
max_bin = random.randint(100,500)
temp_pop.append(max_bin)
temp_v.append(random.randint(-3,3))
bagging_freq = random.randint(1,10)
temp_pop.append(bagging_freq)
temp_v.append(random.randint(-3,3))
feature_fraction_seed = random.randint(1,10)
temp_pop.append(feature_fraction_seed)
temp_v.append(random.randint(-3,3))
min_data_in_leaf = random.randint(1,20)
temp_pop.append(min_data_in_leaf)
temp_v.append(random.randint(-3,3))
pop.append(temp_pop) # 初始种群
V.append(temp_v) # 初始化速度
# 计算适应度
fitness.append(evaluate(train1,feature_use ,temp_pop)) # 染色体的适应度 end
pop = np.array(pop)
V = np.array(V)
# 个体极值和群体极值
bestfitness =min(fitness)
bestIndex = fitness.index(bestfitness)
zbest=pop[bestIndex,:] #全局最佳
gbest=pop #个体最佳
fitnessgbest=fitness #个体最佳适应度值
fitnesszbest=bestfitness #全局最佳适应度值开始迭代寻优:
count = 0
## 迭代寻优
for i in range(maxgen):
for j in range(sizepop):
count = count + 1
print(count)
# 速度更新
V[j,:] = V[j,:] + c1 * random.random() * (gbest[j,:] - pop[j,:]) + c2 * random.random() * (zbest - pop[j,:])
if(V[j,0]<-0.1):
V[j,0]=-0.1
if(V[j,0]>0.1):
V[j,0]=0.1
if(V[j,1]<-0.02):
V[j,1]=-0.02
if(V[j,1]>0.02):
V[j,1]=0.02
if(V[j,2]<-0.1):
V[j,2]=-0.1
if(V[j,2]>0.1):
V[j,2]=0.1
if(V[j,3]<-0.1):
V[j,3]=-0.1
if(V[j,3]>0.1):
V[j,3]=0.1
if(V[j,4]<-2):
V[j,4]=-2
if(V[j,4]>2):
V[j,4]=2
if(V[j,5]<-10):
V[j,5]=-10
if(V[j,5]>10):
V[j,5]=10
if(V[j,6]<-5):
V[j,6]=-5
if(V[j,6]>5):
V[j,6]=5
if(V[j,7]<-1):
V[j,7]=-1
if(V[j,7]>1):
V[j,7]=1
if(V[j,8]<-1):
V[j,8]=-1
if(V[j,8]>1):
V[j,8]=1
if(V[j,9]<-1):
V[j,9]=-1
if(V[j,9]>1):
V[j,9]=1
pop[j,:]=pop[j,:]+0.5*V[j,:]
if(pop[j,0]<0):
pop[j,0]=0.001
if (pop[j, 0] > 1):
pop[j, 0] = 0.9
if (pop[j, 1] < 0):
pop[j, 1] = 0.001
if (pop[j, 1] > 0.2):
pop[j, 1] = 0.2
if (pop[j, 2] < 0.5):
pop[j, 2] = 0.5
if (pop[j, 2] > 1):
pop[j, 2] = 1
if (pop[j, 3] < 0.3):
pop[j, 3] = 0.3
if (pop[j, 3] > 1):
pop[j, 3] = 1
if (pop[j, 4] < 3):
pop[j, 4] =3
if (pop[j, 4] > 100):
pop[j, 4] = 100
if (pop[j, 5] < 800):
pop[j, 5] = 800
if (pop[j, 5] > 1200):
pop[j, 5] = 1200
if (pop[j, 6] < 100):
pop[j, 6] = 100
if (pop[j, 6] > 500):
pop[j, 6] = 500
if (pop[j, 7] < 1):
pop[j, 7] = 1
if (pop[j, 7] > 10):
pop[j, 7] = 10
if (pop[j, 8] < 1):
pop[j, 8] = 1
if (pop[j, 8] > 10):
pop[j, 8] = 10
if (pop[j, 9] < 1):
pop[j, 9] = 1
if (pop[j, 9] > 20):
pop[j, 9] = 20
fitness[j] = evaluate(train1,feature_use,pop[j,:])
for k in range(1,sizepop):
if(fitness[k] > fitnessgbest[k]):
gbest[k,:] = pop[k,:]
fitnessgbest[k] = fitness[k]
#群体最优更新
if fitness[k] > fitnesszbest:
zbest = pop[k,:]
fitnesszbest = fitness[k]载入参数进行预测:
# 采用lgb回归预测模型,具体参数设置如下
model_lgb = lgb.LGBMRegressor(objective=‘regression‘,
min_sum_hessian_in_leaf=zbest[0],
learning_rate=zbest[1],
bagging_fraction=zbest[2],
feature_fraction=zbest[3],
num_leaves=int(zbest[4]),
n_estimators=int(zbest[5]),
max_bin=int(zbest[6]),
bagging_freq=int(zbest[7]),
feature_fraction_seed=int(zbest[8]),
min_data_in_leaf=int(zbest[9]),
is_unbalance=True)
targetme=train1[‘target‘]
model_lgb.fit(train1[feature_use].fillna(-1), train1[‘target‘])
y_pred = model_lgb.predict(test1[feature_use].fillna(-1))
print("lgb success")上文中的 train是 pandas中的dataframe类型,下图为这个代码运行起来的情况
有技术交流的可以扫描以下
以上是关于集成学习lgb库调参的粒子群方法的主要内容,如果未能解决你的问题,请参考以下文章
机器学习系列调参GridsearchCV随机森林GBDTLightGBM和XGBoost调参顺序,外加一些加速调参的小技巧(主要介绍坐标下降)