矩阵乘法
Posted yu-liang
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵乘法相关的知识,希望对你有一定的参考价值。
一.C=A*B
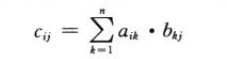
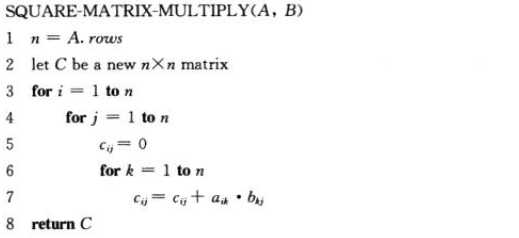
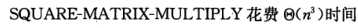

1 #矩阵乘法 O(n*3) 2 def square_matrix_multiply(A,B): 3 C = [] 4 n = len(A)#A的阶 5 C = [[0 for col in range(n)] for row in range(n)]#生成n*n的全0矩阵 6 for i in range(0,n): 7 for j in range(0,n): 8 for k in range(0,n): 9 C[i][j]=C[i][j]+A[i][k]*B[k][j]#矩阵乘法规则 10 return C 11 A=[[1,3],[7,5]] 12 B=[[6,8],[4,2]] 13 print(square_matrix_multiply(A, B)) 14 -------------------------------------------- 15 [[18, 14], [62, 66]]
二.Strassen算法



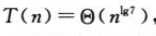

1 #递归分治法-矩阵乘法 2 def square_matrix_multiply_recursive(A, B): 3 n = len(A) 4 C = [[0 for col in range(n)] for row in range(n)] 5 if n == 1: 6 C[0][0] = A[0][0] * B[0][0] 7 else: 8 (A11, A12, A21, A22) = partition_matrix(A) 9 (B11, B12, B21, B22) = partition_matrix(B) 10 (C11, C12, C21, C22) = partition_matrix(C) 11 C11 = add_matrix(square_matrix_multiply_recursive(A11, B11), square_matrix_multiply_recursive(A12, B21)) 12 C12 = add_matrix(square_matrix_multiply_recursive(A11, B12), square_matrix_multiply_recursive(A12, B22)) 13 C21 = add_matrix(square_matrix_multiply_recursive(A21, B11), square_matrix_multiply_recursive(A22, B21)) 14 C22 = add_matrix(square_matrix_multiply_recursive(A21, B12), square_matrix_multiply_recursive(A22, B22)) 15 C = merge_matrix(C11, C12, C21, C22) 16 return C 17 18 #分解矩阵,把矩阵分成4分 19 def partition_matrix(A): 20 n = len(A) 21 n2 = int(n / 2) 22 #生成四个初始零矩阵 23 A11 = [[0 for col in range(n2)] for row in range(n2)] 24 A12 = [[0 for col in range(n2)] for row in range(n2)] 25 A21 = [[0 for col in range(n2)] for row in range(n2)] 26 A22 = [[0 for col in range(n2)] for row in range(n2)] 27 #给这四个矩阵赋值 28 for i in range(0, n2): 29 for j in range(0, n2): 30 A11[i][j] = A[i][j] 31 A12[i][j] = A[i][j + n2] 32 A21[i][j] = A[i + n2][j] 33 A22[i][j] = A[i + n2][j + n2] 34 return (A11, A12, A21, A22) 35 36 #合并矩阵,把四个矩阵合并为一个 37 def merge_matrix(A11, A12, A21, A22): 38 n2 = len(A11) 39 n = 2 * n2 40 A = [[0 for col in range(n)] for row in range(n)] 41 for i in range(0, n): 42 for j in range(0, n): 43 if i <= (n2 - 1) and j <= (n2 - 1): 44 A[i][j] = A11[i][j] 45 elif i <= (n2 - 1) and j > (n2 - 1): 46 A[i][j] = A12[i][j - n2] 47 elif i > (n2 - 1) and j <= (n2 - 1): 48 A[i][j] = A21[i - n2][j] 49 else: 50 A[i][j] = A22[i - n2][j - n2] 51 return A 52 53 #添加矩阵,把A 和 B对应添加进一个矩阵C 54 def add_matrix(A, B): 55 n = len(A) 56 C = [[0 for col in range(n)] for row in range(n)] 57 for i in range(0, n): 58 for j in range(0, n): 59 C[i][j] = A[i][j] + B[i][j] 60 return C 61 62 A=[[1,3],[7,5]] 63 B=[[6,8],[4,2]] 64 C=square_matrix_multiply_recursive(A,B) 65 print(C) 66 ---------------------------------------------------------- 67 [[18, 14], [62, 66]]
以上是关于矩阵乘法的主要内容,如果未能解决你的问题,请参考以下文章
