排序算法---堆排序

Posted 2020-11-17 lliuye

github：代码实现
本文算法均使用python3实现

---

1. 什么是堆

??堆（heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象，且堆总是一棵完全二叉树。由于堆是基于完全二叉树的结构，因此可以使用顺序存储结构即数组来保存堆，再根据堆的性质，我们可以得到该数组（从0下标开始）的一些性质：
??（1）对于数组 $ heap $ 中的第 $ i $ 个节点，其左孩子节点值 $ heap[2i+1] leq heap[i] $ 且其右孩子节点值 $ heap[2i+2] leq heap[i] $ ，此时为大根堆。（父亲值大于等于孩子值）
??（2）对于数组 $ heap $ 中的第 $ i $ 个节点，其左孩子节点值 $ heap[2i+1] geq heap[i] $ 且其由孩子节点值 $ heap[2i+2] geq heap[i] $ ，此时为小根堆。（父亲值小于等于孩子值）

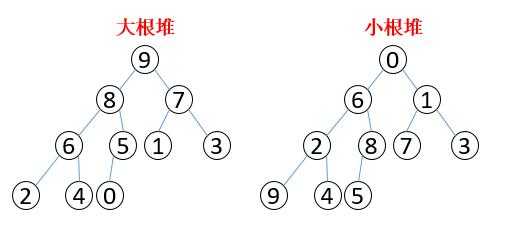
??对于大根堆，将其映射到数组中如下：

---

2. 如何构建初始堆

??堆的构建是一个递归的过程。下面以大根堆为例进行讲解。具体操作如下：
??构建初始大根堆：从最后一个非叶子节点开始，比较其与其左右孩子值的大小，若其节点值比孩子节点值小，则将其与较大孩子进行交换。然后依次对其它节点进行如此比较与交换，直至根节点，此时根节点的值即为该堆中的最大值。

---

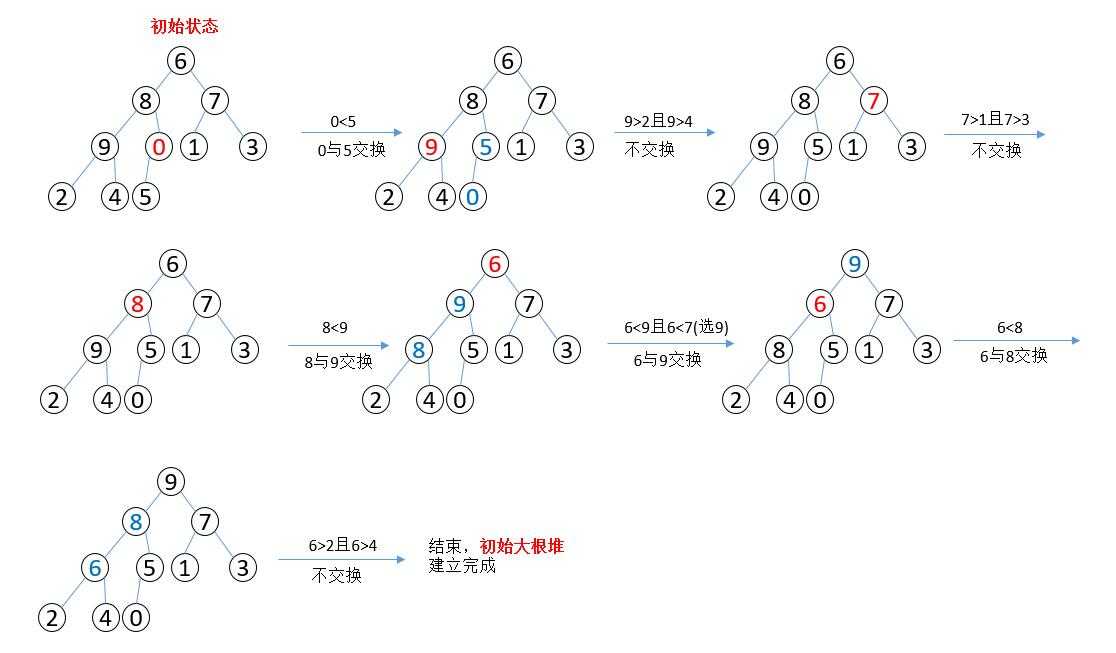
3. 如何进行堆排序

??堆排序是在已经构建好的初始大根堆上进行。主要分为以下几步：
??（1）对初始序列构建初始大根堆。（按照2中所描述）
??（2）将大根堆的根节点值与最后一个节点值交换。

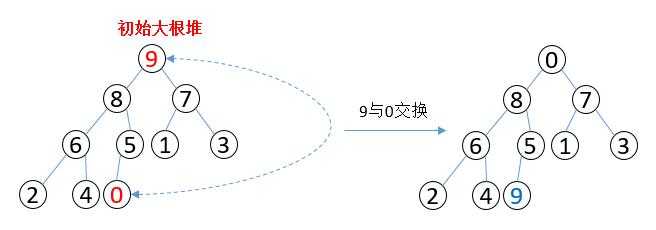
??（3）将交换后的堆从数组上分为两个区：无序区与有序区。对无序区进行“堆调整”，即将无序区调整为大根堆。（其实建立初始大根堆也是一个不断调用“堆调整”的过程）

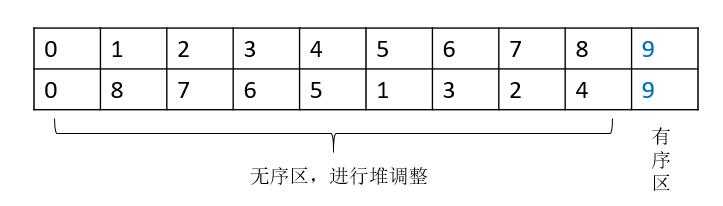
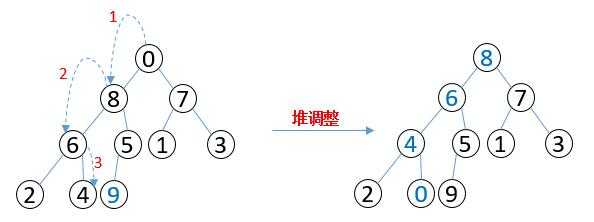
??（4）将无序区中的根节点值与无序区中的最后一个节点值进行交换。此时无序区长度减 $ 1 $ ，有序区长度加 $ 1 $ ，见下图。重复（3）直到无序区中只有一个节点为止。

---

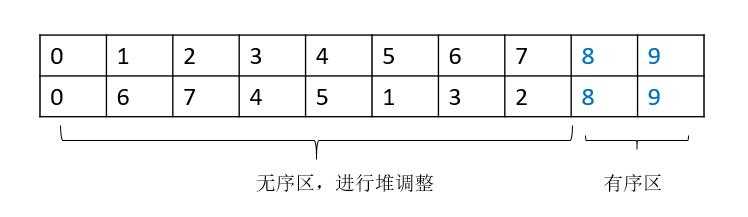
4. 实现代码

class HeapSort:
    '''堆排类'''
    def Max_Heapify(self, heap, heapsize, root):
        '''堆调整，使得根节点值大于子节点值'''
        left = root * 2 + 1  # 列表从0开始，左节点下标为 2i+1,右节点下标为 2i+2
        right = left + 1
        larger = root
        if left < heapsize and heap[left] > heap[larger]:
            larger = left
        if right < heapsize and heap[right] > heap[larger]:
            larger = right
        if larger != root:
            heap[larger], heap[root] = heap[root], heap[larger]
            self.Max_Heapify(heap, heapsize, larger)
        else: return 

    def Build_Max_Heap(self, heap):
        '''构建初始大根堆'''
        heapsize = len(heap)
        for i in range((heapsize-2)//2, -1, -1):
            # 从最后一个非叶子节点开始构建
            self.Max_Heapify(heap, heapsize, i)

    def Heap_Sort(self, heap):
        '''堆排序'''
        # 步骤（1）构建初始大根堆
        self.Build_Max_Heap(heap)
        for i in range(len(heap)-1, -1, -1):
            # 步骤（2）交换无序区第一个节点值与最后一个节点值
            heap[0], heap[i] = heap[i], heap[0]
            # 步骤（3）对无序区进行“堆调整”
            self.Max_Heapify(heap, i, 0)
        return heap[::-1]

---

5. 算法分析

??堆排序是一种选择排序，且是不稳定排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆的时间复杂度为 $ O(n) $ ，在交换并重建堆的过程中，需进行 $ n-1 $ 次”堆调整”，而重建堆的过程中，根据完全二叉树的性质，$ [log_2(n-1),log_2(n-2)...1] $ 逐步递减，近似为 $ O(n log_2 n) $ 。所以堆排序时间复杂度为是 $ O(n log_2 n) + O(n) = O(n log_2 n) $ 。即堆排序的最坏时间复杂度为 $ O(n log_2 n) $ （平均复杂度接近于最坏情况）。

---

引用及参考：
[1]《数据结构》李春葆著
[2] https://www.cnblogs.com/chengxiao/p/6129630.html
[3] https://blog.csdn.net/minxihou/article/details/51850001

写在最后：本文参考以上资料进行整合与总结，属于原创，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！
若需转载请注明：https://www.cnblogs.com/lliuye/p/9167471.html