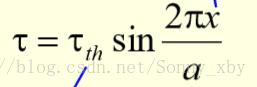MEGNet普适性图神经网络，精确预测分子和晶体性质

Posted 2023-04-05

参考技术A

海归学者发起的公益学术平台

分享信息，整合资源

交流学术，偶尔风月

近年来机器学习算法在包括自然语言处理，图像识别等诸多领域大放异彩。得益于如Materials Project ¹ , QM9 ^{2 , 3} 等材料数据库的不断完善和发展，机器学习正在被越来越多的应用在材料学领域的研究中。然而，由于研究目标的单一性，多数工作仍然局限于解决特定的晶体结构以及特定的材料性质预测问题。一种泛化的，普适性的机器学习模型仍然是材料学领域研究的重点目标。此研究是基于

基于DeepMind建立的图神经网络框架。

在材料学领域，对分子或晶体结构的特征描述需要满足平移，转动，镜面不变性，以及对整体结构特异信息的表征。常见的结构特征描述由于其局域性，缺乏对整体结构信息的表达，因而不具有普适性。图网络模型(graph-network)是一种基于图论的结构化模型，从理论上完美解决了这一问题。在图论中，图(graph)由若干给定的顶点(node)及连接顶点的边(edge)构成。运用到分子(或晶体)结构中，原子(atom)可以由顶点(node)描述，连接原子之间的化学键(bond)可以由边(edge)描述，从而可以把一个个分子或晶体结构看作一个个独立的“图”。基于此类模型的结构描述方法，科研工作者可以开发出针对任何材料结构或任何物理化学性质的普适性模型。尽管具有理论可行性，此类模型由于模型复杂度，材料数据量的限制，仍很少被应用在材料学领域中 ^{4 , 5} 。近日，UC San Diego 的 Shyue Ping Ong 课题组基于DeepMind建立的图神经网络框架 ⁶ ，开发了一套分子和晶体通用性质预测模型(MEGNet)，在各项性质预测测试中达到了领先水平 ⁷ 。

图 1. MEGNet 概述。每个分子/晶体结构由化学键信息，原子信息，和状态信息描述。每个结构描述输入模型后，依次更新，直到总的结构输出性质与DFT计算值接近。

图1中描述了该模型的工作模式： 每个结构可用三个向量表征，分别包含原子信息，化学键信息，和状态函数信息。在每一次模型训练迭代中，依次更新化学键向量，原子向量，和状态函数向量，得到新的结构表征向量，直到通过该表征输出的性质与DFT计算结果趋于一致。作者首先用QM9 分子数据集中超过130k数据作为训练集训练模型，并用得到的模型预测分子中的13项物理化学性质，在其中的11项中达到同类模型中的最优结果（表1）。更为先进的是，之前的工作对由状态参数关联的状态函数，如内能（U ₀ , U），焓(H)，和吉布斯自由能(G)，采用的是分别训练模型进行预测的方法。

然而本工作中，作者采用加入状态参数作为输入的方法，可由单一模型同时预测U ₀ , U, H和G，并保持与分别模型训练类似的准确度，大大提高了训练效率[YZ1] 。在针对晶体结构的应用中，作者用Materials Project数据库中超过69k数据作为训练集，针对生成能，能带带隙，体积模量和剪切模量进行了回归（Regression）分析，并用带隙值作为金属和非金属的判据进行分类(classification)分析。回归分析中的平均绝对误差（MAE）低于同类型模型SchNet ⁴ 和CGCNN ⁵ （表2），金属和非金属分类分析中综合准确率达86.9%，ROC中AUC达到0.926，与此前最优模型CGCNN类似。

表1. 不同模型在QM9上预测13项性质的平均绝对误差（MAE）对比

表2. MEGNet和其他基于图像模型

在Materials Project数据集的预测准确度对比

在对模型的深入分析中，作者发现，从最优模型中提取出的元素映射（embedding）与化学常识吻合。例如，将元素映射投影二维空间可发现，Eu和Yb与其他镧系元素距离较远，而与碱土金属更接近，这与化学经验相符。这样的分析一方面佐证了模型可以学习到可靠的化学信息，另一方面可将学习到的化学信息用于迁移学习，以大大降低训练新模型训练所需数据量。例如，在此例中，作者通过用~69k生成热的数据训练的模型提取的元素映射，用于预测带隙和弹性性质的模型训练，后者的数据量只有生成热的一半甚至十分之一。通过迁移学习的方法作者得到比直接训练更低的MAE和提高两倍的收敛速度。这为小数据量的性质的高效准确模型训练提供了可行的方案。

在模型的使用方面，用户可登陆http://megnet.crystals.ai，根据提示输入晶体结构编码或cif文件即可得到模型预测的性质。另外，文章所涉及的Python代码均已开源（https://github.com/materialsvirtuallab/megnet.git）。下面示例如何使用已有模型和训练新的模型。

1 示例一： 使用分子模型

2 示例二：使用晶体模型预测剪切模量

3 示例三：训练新模型

参考文献

(1) Jain, A.; Ong, S. P.; Hautier, G.; Chen, W.; Richards, W. D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater . 2013, 1 (1), 011002. https://doi.org/10.1063/1.4812323.

(2) Ruddigkeit, L.; van Deursen, R.; Blum, L. C.; Reymond, J.-L. Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17. J. Chem. Inf. Model. 2012, 52 (11), 2864–2875. https://doi.org/10.1021/ci300415d.

(3) Ramakrishnan, R.; Dral, P. O.; Rupp, M.; von Lilienfeld, O. A. Quantum Chemistry Structures and Properties of 134 Kilo Molecules. Sci. Data 2014, 1, 140022. https://doi.org/10.1038/sdata.2014.22.

(4) Schütt, K. T.; Sauceda, H. E.; Kindermans, P.-J.; Tkatchenko, A.; Müller, K.-R. SchNet – A Deep Learning Architecture for Molecules and Materials. J. Chem. Phys . 2018, 148 (24), 241722. https://doi.org/10.1063/1.5019779.

(5) Xie, T.; Grossman, J. C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120 (14), 145301. https://doi.org/10.1103/PhysRevLett.120.145301.

(6) Battaglia, P. W.; Hamrick, J. B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R.; et al. Relational Inductive Biases, Deep Learning, and Graph Networks. ArXiv 180601261 Cs Stat 2018.

(7) Chen, C.; Ye, W.; Zuo, Y.; Zheng, C.; Ong, S. P. Graph Networks as a Universal Machine Learning Framework for Molecules and Crystals. Chem. Mater . 2019. https://doi.org/10.1021/acs.chemmater.9b01294.

扩展阅读

npj: 机器学习—快速精确预测电子结构问题

npj: 深度学习预测—杂化石墨烯-氮化硼对构型的带隙

npj: 高熵合金—基于第一性原理的屈服强度预测

npj: 机器学习—神经网络方法计算多组分晶体的形成能

本文系网易新闻·网易号“各有态度”特色内容

媒体转载联系授权请看下方

工程材料之金属形变理论基础

注：内容参考至东北大学机械学院何雪浤老师课件

一、金属的晶体结构

　　塑性变形或破坏均沿着某一特定的面或方向，可知结晶构造和材料强度之间有着密切的关系。

1.基本概念

（1）晶体与非晶体

　　晶体是组成物质的原子、离子和分子有规则排列

　　非晶体是组成物体的原子、离子和分子无规则地堆积在一起

　　理想晶体：质点严格按照空间点阵排列

　　实际晶体：存在着各种各样的结构的不完整性

（2）空间点阵

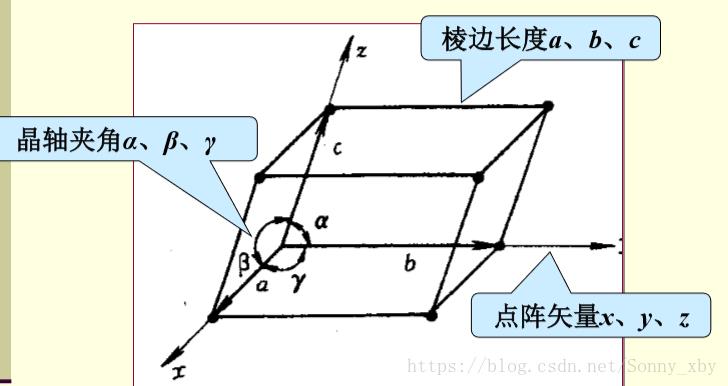
　　定义：将晶体中质点排列情况抽象为有规则地排列与空间的几何点，即空间点阵，

　　表达：

?

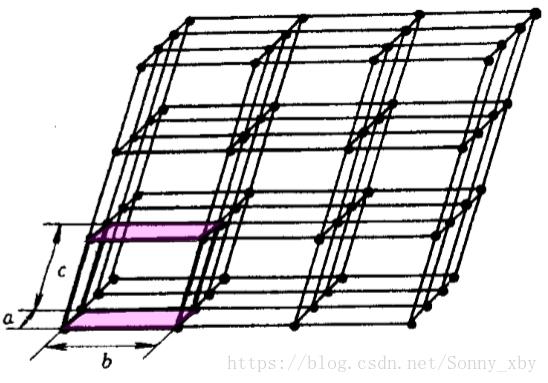
　　几何量：棱边长、晶轴夹角、点阵矢量

?

　　点阵常数：晶胞中每条棱边的长度即为点阵常数，或称晶格常数。

（3）晶胞

　　空间点阵中选择一个小的平行四边形作为基本单元，成为晶胞或晶格。

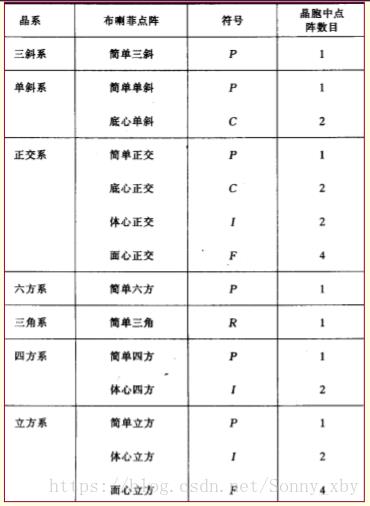
（4）晶系

?

（5）布莱菲点阵

?

?

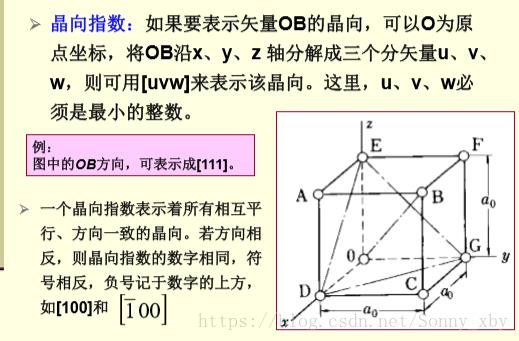
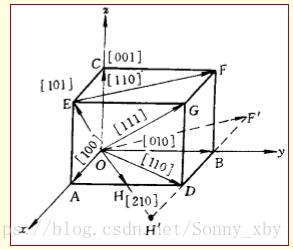
（6）晶向和晶向指数

　　定义：晶体中由物质质点所连城的直线

　　标定：Miller指数——晶向指数

?

　　晶向族：因对称关系而等同的各组晶向可归为一个晶向族，例如对于立方晶系如下图

?

　　图中，OA、OB、OC方向的晶向可表示为?，由于这几个方向的性质一致，故都可以用<100>来表示。

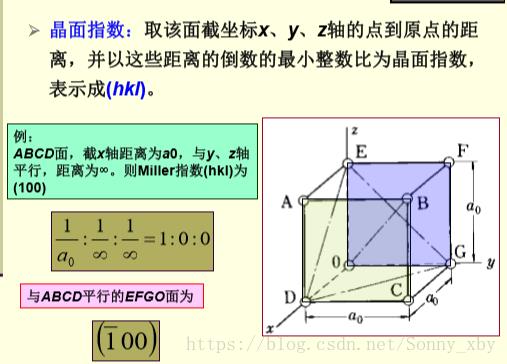
（7）晶面和晶面指数

　　定义：晶体中由物质质点所组成的平面

　　标定：Miller指数——晶面指数，即

?

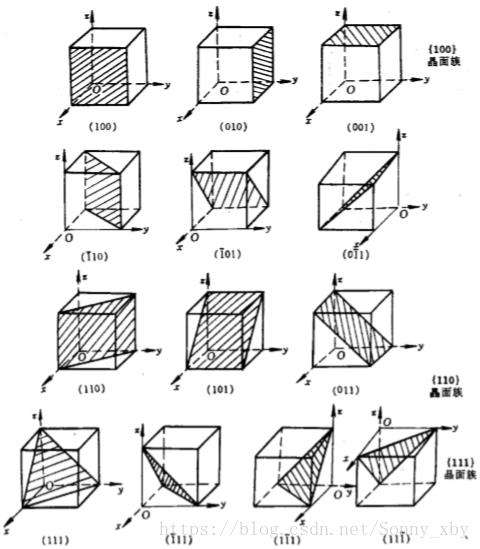
　　晶面族：当晶面上的原子排列情况和面间距等相同，可归为一个晶面族。

?

　　如图中，<100>,<110>,<111>等皆为晶面族。

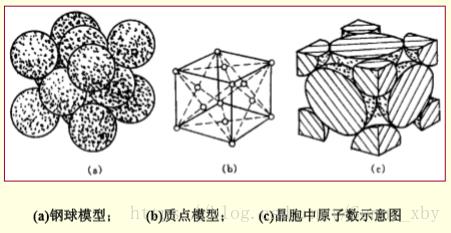
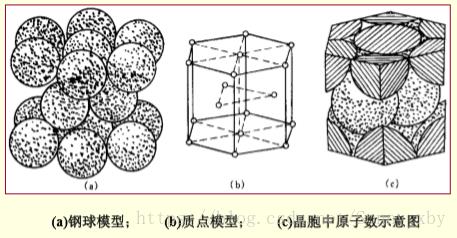
2.典型的晶体结构

	体心立方结构	面心立方结构	密排六方结构
简写	Bcc	fcc	Hcp
晶胞模型	?	?	?
晶胞原子数	2	4	6
点阵常数	a=(2/√3)?d	a=√2?d
配位数	8	12	12
致密度	0.68	0.74	0.74
间隙	八面体间隙3个 四面体间隙6个	八面体间隙4个 四面体间隙8个	八面体间隙4个 四面体间歇8个
最密排面	{110}	{111}	{0001}
最密排方向	<111>	<110>	?
代表金属	a-Fe,V,Cr,Mo,W等	r-Fe,Cu,Ag,Au,Pt等	Zn、Cd、α—Ti等

3.各向异性

　　定义：沿晶格不同方向，原子排列的周期性和疏密程度不尽相同，由此导致晶体在不同方向的物理化学特性不同。

　　但工业使用的金属材料，一般不具有各向异性的特征。

4.晶体的原子堆垛方式和间隙

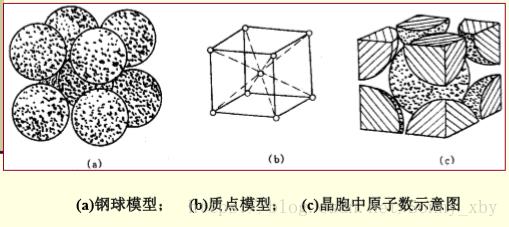
　　（1）晶体中原子堆垛方式

　　最紧密堆积原理：晶体中各离子间的相互结合，可以看作是球体的堆积，球体堆积的密度越大，系统的势能越低，晶体越稳定。

　　金属晶体中原子是以紧密堆积的形式存在的。在一层中，最紧密的堆积方式，是一个球与周围六个球相切，在中心周围形成6个凹位，如下图，ABCA,ABAB。

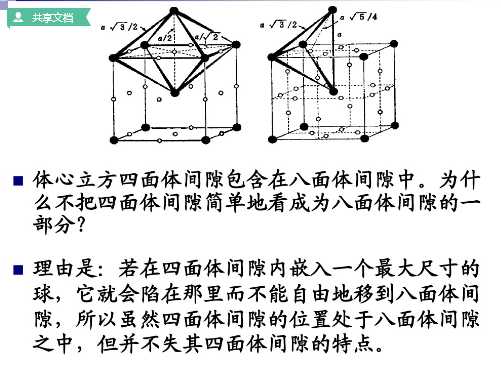
　　（2）晶体中原子间的间隙

　　空隙有两种，四面体间隙（由4个球所构成，球心连线构成一个四面体）和八面体间隙（由6个球体构成，球心连线形成一个八面体）

 

二、晶体缺陷

	点缺陷	线缺陷	面缺陷
定义	零维缺陷	一维缺陷	二维缺陷
形式	空位：在应有原子处出现了空隙 间隙原子：在晶格中间插入的原子 杂质原子：分为置换型和侵入型	刃型位错：滑移区与未滑移区在滑移面上的交界线，常用表示； 螺型位错：原子数目未变，左右不分滑移一个原子间距	晶体表面是一种缺陷，分为晶界和相界。 （1）晶界：单相晶体不同晶粒之间的界面（主要） 1）孪晶界：两晶体或一个晶体两个部分沿一个公共晶面结合起来而保持镜面对称的位向关系。 2）平移晶界（堆垛层错、反相畴界和结晶切变面）：堆垛顺序出错 3）晶粒间界：以任意取向关系相交接的两晶粒间的界面 （2）相界：合金组织不同相之间的界面 1)共格相界 界面上原子同时处于两相晶格节点上 2)部分共格相界 两种相点阵常数不同，依靠刃型位错保持匹配 3）非共格相界：完全没有共格关系
机理	自然状态下原子处于动平衡状态，温度越高，原子振动越厉害，可能会摆脱原子束缚而脱离平衡位置。 Schottky缺陷：离开平衡位置的原子迁移至晶体表面的正常格点位置，而晶体内仅留有空位，晶体中形成肖特基缺陷（特点是晶体体积膨胀，密度下降） Frankel缺陷：离开平衡位置的原子进入晶格的间隙位置（特点是空位和间隙原子同时出现，晶体体积不发生变化，晶体不会因为出现空位而产生密度变化）
原因	过度族金属元素形成化合物时可能产生空位 某些金属发生氧化时金属原子外迁 金属受力塑性变形导致位错线互相交割 高能粒子轰击产生空位和间隙原子	位错不能终止在晶体内部，但可终止在晶体表面。在内部，位错只能以封闭环形式存在。 两个变形程度不同的区域的分界必存在位错； 位错附近变形大，是晶体中内应力场的源
特点	点缺陷处于动平衡 点缺陷重要影响是扩散 对金属高温下的行为有重要作用。
材料行为	1）结构变化：晶格畸变（如空位引起晶格收缩，间歇原子引起晶格膨胀，置换原子可引起收缩或膨胀）；形成其他晶体缺陷（如过饱和的空位可集中形成内部的的空洞，集中一片的塌陷形成位错） 2.性能变化：物理性能：如电阻率增大，密度减小。力学性能：屈服强度提高（间歇原子和异类原子的存在会增加位错的运动阻力），加快原子的扩算迁移。	对材料的力学行为如塑性变形、强度、断裂等都起着决定性的作用，对材料的扩散、相变过程又较大的影响。

 

 ·简述晶体缺陷与材料性能之间的关系

 

　　（1）点缺陷对材料性能的影响

晶体中点缺陷的不断无规则运动和空位与间歇原子不断产生与复合是晶体中许多物理过程如扩散、相变等过程的基础。空位是金属晶体结构中故有的点缺陷，空位会与原子交换位置造成原子的热激活运输，空位的迁移直接影响原子的热运输，从而影响材料的电、热、磁等工程性能。晶体中点却像存在一方面造成点阵畸变，使晶体内能升高，增加了晶体热力学不稳定性，另一方面增大了原子排列的混乱程度，改变了周围原子的振动频率。使熵值增大，使晶体稳定。在一般情形下，点缺陷主要影响晶体的物理性质，如比容、比热容、电阻率等。

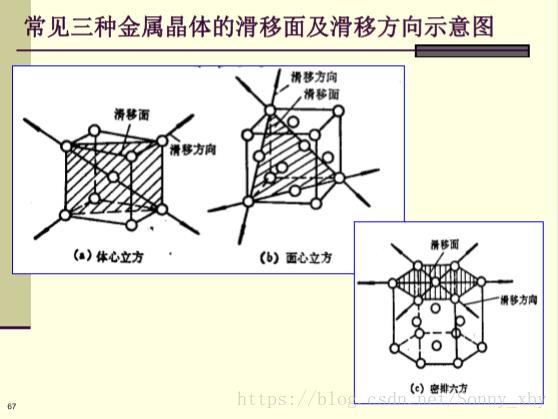
三、滑移变形

?

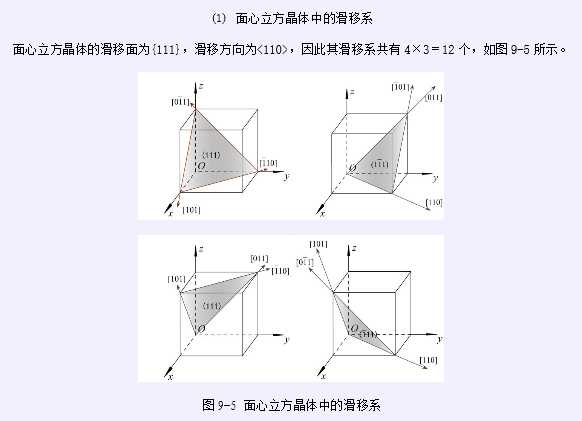
1.滑移系

　　（1）滑移：金属在切应力作用下沿着一定的晶面和一定的晶向进行的切变过程。?

　　（2）滑移方向：上述滑动的晶向称为滑移方向，在原子间隔最小的方向

　　（3）滑移面：上述滑移的晶面称为滑移面，一般是原子密度最高的结晶面。面间间隔最大，对滑移的抵抗最小。

　　（4）滑移线：滑移变形的结果是在试样表面出现滑移线。?

　　（5）很少的滑移系标志着晶体极端的取向性和很差的塑性，众多的滑移系标志优良的塑性。

?

2.临界分切应力

　　定义：使金属晶体产生滑移所需要的分切应力，称为临界分切应力，也成理论切变强度。

?3.滑移系与材料性能之间的关系

　　滑移系表明了晶体滑移时的可能空间取向，一般来说，在其他条件相同时，滑移系数量越多，滑移过程就越容易进行从而金属的塑性就越好。晶体结构不同时，其滑移系也不同。