朴素贝叶斯学习

Posted 2020-11-17 sxytalent

 

朴素贝叶斯，为什么叫“朴素”，就在于是假定所有的特征之间是“独立同分布”的。这样的假设肯定不是百分百合理的，在现实中，特征与特征之间肯定还是存在千丝万缕的联系的，但是假设特征之间是“独立同分布”，还是有合理性在里面，而且针对某些特定的任务，用朴素贝叶斯得到的效果还不错，根据“实践是检验真理的唯一标准”，这个模型就具备意义了。这其实和那个“马尔科夫”假设有类似的地方。

朴素贝叶斯的一个思想是，根据现有的一些材料，通常叫做训练语料，这些语料包含很多信息，而这些现实中的信息会蕴含着某种规律，朴素贝叶斯就是一个不是十分完美，但效果也还过得去的拟合这个潜在的规律的一个模型。

比如，现在现实中有女孩子所选择的老公的情况，从这些情况信息中，我们可以试图用朴素贝叶斯这一模型来找出女生选择老公的规律（当然，不是一个百分百准确的规律，但准确性过得去）。

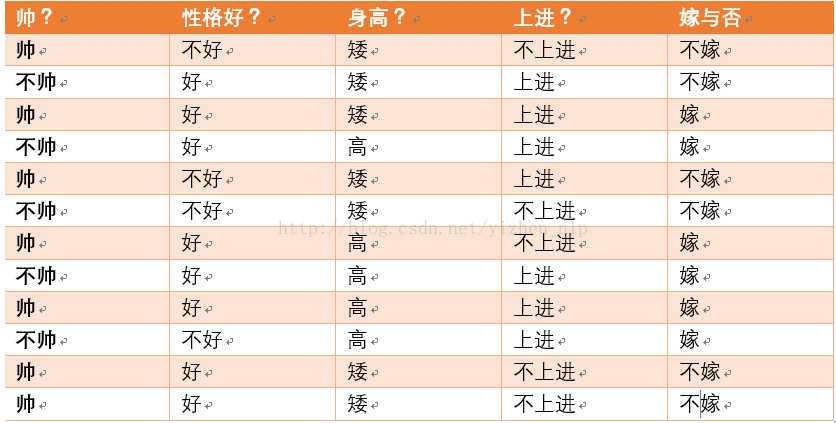
而朴素贝叶斯的核心思想就是：针对某一个实际中的男生，他的四个特征分别为:x1,x2,x3,x4，如果p(嫁|x1,x2,x3,x4)>p(不嫁|x1,x2,x3,x4)，这说明这个男生大概率情况下会有女生愿意嫁他，反之则是大概率不嫁

而根据贝叶斯公式：

 

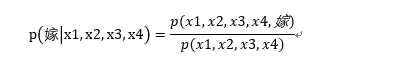
而根据朴素贝叶斯的假设，特征之间是“独立同分布”的，所以，上面的公式可以写为：

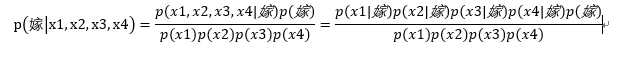
而p(x1),p(x2),p(x3),p(x4),p(嫁),p(x1|嫁)，p(x2|嫁)，p(x3|嫁)，p(x4|嫁)根据训练语料，可以轻松求得，因此p(嫁|x1,x2,x3,x4)>p(不嫁|x1,x2,x3,x4)与否这一问题就可以得到答案

假设，现在有一个男生的特征是：不帅，性格不好，矮，不上进，那么所需要的几个概率分别为：

p(不帅)=5/12，p(性格不好)=4/12，p（矮）=7/12，p（不上进）=5/12，P（嫁）=6/12.

p(不帅|嫁)=3/12,p(性格不好|嫁)=1/12,p(矮|嫁)=1/12,p(不上进|嫁)=1/12

因此：p(嫁|x1,x2,x3,x4)=3/12*1/12*1/12*1/12*6/12  /   ( 5/12*4/12*7/12*5/12 )=3/1400=0.0021

而p(不嫁|x1,x2,x3,x4)=72/700=0.103，

显然，这个男生大概率情况下不会有女生愿意嫁他

具体的代码实现如下，这里随机产生10个男生的情况，根据训练语料判断他们是否大概率情况下有女生愿意嫁他们

分别用python代码和java代码实现，其中，java的逻辑上有一点小小的问题，虽然也能得到正确的结果

1 #Import Library of Gaussian Naive Bayes model  
 2 from sklearn.naive_bayes import GaussianNB  
 3 import random  
 4 import codecs
 5 
 6 f=codecs.open("trainData.txt",‘r‘,‘utf-8‘)
 7 a=[]
 8 b=[]
 9 for l in f:
10     temp=l.split()
11     i=0
12     for m in temp:
13         if m.find("不"):
14             temp[i]=0
15             i+=1
16         elif m.find("高"):
17             temp[i]=1
18             i+=1
19         elif m.find("矮"):
20             temp[i]=0
21             i+=1
22         else:
23             temp[i]=1
24             i+=1
25     a.append(temp[:4])
26     b.append(temp[-1])
27 #Create a Gaussian Classifier  
28 model = GaussianNB()  
29   
30 # Train the model using the training sets   
31 model.fit(a, b)  
32 for i in range(0,9):
33     if random.random()>0.5:  
34         x1=1
35         s1="帅" 
36     else:
37         x1=0
38         s1="不帅"
39     if random.random()>0.5:
40         x2=1
41         s2="性格好"
42     else:
43         x2=0
44         s2="性格不好"
45     if random.random()>0.5:
46         x3=1
47         s3="高"
48     else:
49         x3=0
50         s3="矮"
51     if random.random()>0.5:
52         x4=1
53         s4="上进"
54     else:
55         x4=0
56         s4="不上进"
57     predicted= model.predict([[x1,x2,x3,x4]]) 
58     if 0 in predicted:
59         print(s1,s2,s3,s4,"不嫁")
60     else:
61         print(s1,s2,s3,s4,"嫁")

 

JAVA代码：

  1 package bayesTest;
  2 
  3 import java.io.*;
  4 
  5 public class bayesTest {
  6 
  7     public static void main(String[] args) throws IOException {
  8 
  9          FileReader reader = new FileReader("Data\\trainData.txt");  
 10          BufferedReader br = new BufferedReader(reader);  
 11          String str = null;  
 12          int countHansome=0,countUnHansome=0,countChaGood=0,countChaBad=0,countHigh=0,countShort=0,countAggre=0,
 13                  countUnAggre=0;
 14          int feature[][]=new int[4][2];
 15          int feature2[][]=new int[4][2];
 16          int lineNum=0;
 17          int location1,location2,location3,location4,location5;
 18          int x1,x2,x3,x4,x5;
 19          int m1,m2,m3,m4,m5;
 20          String s1=null,s2=null,s3=null,s4=null;
 21          double answer1,answer2;
 22          int marryCount=0;
 23          while((str = br.readLine()) != null){
 24              location5=str.indexOf("不嫁");
 25              if(location5==-1){  //嫁
 26                  marryCount++;
 27              
 28                  location1=str.indexOf("不帅");
 29                  if(location1==-1){  //帅
 30                      feature[0][1]++;
 31                  }else{
 32                      feature[0][0]++;
 33                  }
 34                  location2=str.indexOf("不好");
 35                  if(location2==-1){//好
 36                      feature[1][1]++;
 37                  }else{
 38                      feature[1][0]++;
 39                  }
 40                  location3=str.indexOf("矮");
 41                  if(location3==-1){//高
 42                      feature[2][1]++;
 43                  }else{
 44                      feature[2][0]++;
 45                  }
 46                  location4=str.indexOf("不上进");
 47                  if(location4==-1){//上进
 48                      feature[3][1]++;
 49                  }else{
 50                      feature[3][0]++;
 51                  }
 52                  }else{
 53                      location1=str.indexOf("不帅");
 54                      if(location1==-1){  //帅
 55                          feature2[0][1]++;
 56                      }else{
 57                          feature2[0][0]++;
 58                      }
 59                      location2=str.indexOf("不好");
 60                      if(location2==-1){//好
 61                          feature2[1][1]++;
 62                      }else{
 63                          feature2[1][0]++;
 64                      }
 65                      location3=str.indexOf("矮");
 66                      if(location3==-1){//高
 67                          feature2[2][1]++;
 68                      }else{
 69                          feature2[2][0]++;
 70                      }
 71                      location4=str.indexOf("不上进");
 72                      if(location4==-1){//上进
 73                          feature2[3][1]++;
 74                      }else{
 75                          feature2[3][0]++;
 76                      }
 77                  }
 78              lineNum++;
 79          }
 80          
 81          //p(嫁|x1,x2,x3,x4)=p(x1|嫁)*p(x2|嫁)*p(x3|嫁)*p(x4|嫁)*p(嫁)/p(x1)*p(x2)*p(x3)*p(x4)
 82          for(int i=0;i<10;i++){
 83              x1=Math.random()>0.5?0:1;
 84              switch(x1){
 85              case 0:s1="不帅";break;
 86              case 1:s1="帅";break;
 87              }
 88              x2=Math.random()>0.5?0:1;
 89              switch(x2){
 90              case 0:s2="性格不好";break;
 91              case 1:s2="性格好";break;
 92              }
 93              x3=Math.random()>0.5?0:1;
 94              switch(x3){
 95              case 0:s3="矮";break;
 96              case 1:s3="高";break;
 97              }
 98              x4=Math.random()>0.5?0:1;
 99              switch(x4){
100              case 0:s4="不上进";break;
101              case 1:s4="上进";break;
102              }
103              
104             
105              
106              answer1=((double)feature[0][x1]/(double)marryCount)*((double)feature[1][x2]/(double)marryCount)*
107                      ((double)feature[2][x3]/(double)marryCount)*((double)feature[3][x4]/(double)marryCount)*
108                      ((double)marryCount/(double)lineNum)/
109                      (((double)(feature[0][x1]+feature2[0][x1])/(double)lineNum)*
110                              ((double)(feature[1][x2]+feature2[1][x2])/(double)lineNum)*
111                              ((double)(feature[2][x3]+feature2[2][x3])/(double)lineNum)*
112                              ((double)(feature[3][x4]+feature2[3][x4])/(double)lineNum));
113              answer2=((double)feature2[0][x1]/(double)marryCount)*((double)feature2[1][x2]/(double)marryCount)*
114                      ((double)feature2[2][x3]/(double)marryCount)*((double)feature2[3][x4]/(double)marryCount)*
115                      ((double)(lineNum-marryCount)/(double)lineNum)/
116                      (((double)(feature[0][x1]+feature2[0][x1])/(double)lineNum)*
117                              ((double)(feature[1][x2]+feature2[1][x2])/(double)lineNum)*
118                              ((double)(feature[2][x3]+feature2[2][x3])/(double)lineNum)*
119                              ((double)(feature[3][x4]+feature2[3][x4])/(double)lineNum));
120              
121             if(answer1>answer2){     
122              System.out.println(s1+","+s2+","+s3+","+s4+","+"要嫁"+answer1+","+answer2);
123              }else{
124                  System.out.println(s1+","+s2+","+s3+","+s4+","+"不嫁"+answer1+","+answer2);
125                 }
126          }
127          
128          
129     }
130 
131 }

 

从这里可以看出，python确实是特别适合用于机器学习当中，代码要简洁得多。