图的割点与割边（超详细！！！）

Posted 2020-11-16 ljy-endl

·割点

割点概念，应该很好理解：

在一个无向图中，如果删除某个顶点，这个图就不再连通（任意两点之间无法相互到达），那么这个顶点就是这个图的割点。 举个例子：

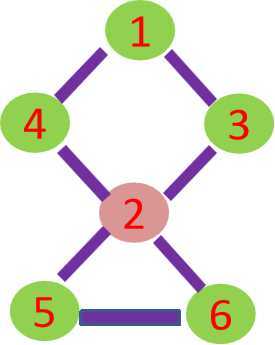
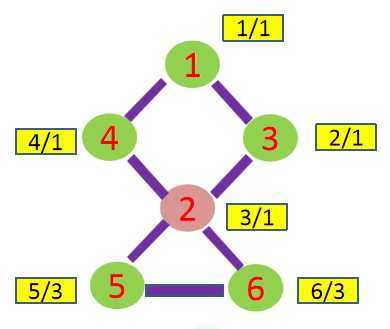
图中的2号顶点就是割点， 删除2号后，4,5不通，1,6也不通等等

如何求割点？

很容易想到的方法是：依次删除每一个顶点，然后用dfs或者bfs来检查图是否依然连通。如果删除某个顶点后，导致图不再连通，那么刚才删除的顶点就是割点。

这种方法的时间复杂度是O(N(N+M))。

下面寻找复杂度低的方法来解决。

首先从图中任意节点开始dfs遍历上图，得到一颗生成树， 如下图，圆圈中数字是顶点编号， 圆圈右上角的数表示这个顶点在遍历时是第几个被访问到的，叫做“时间戳”。

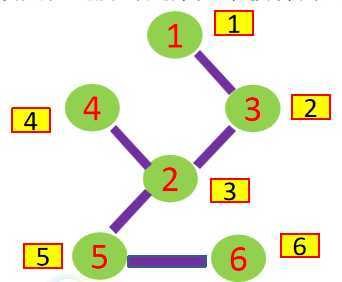
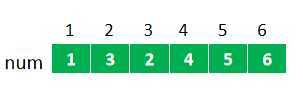
在遍历的时候一定会遇到割点， 关键是如何认定一个顶点是割点呢？？？

在深度优先遍历的时候访问到u（点2）点，此时图被u (点2)分割成两部分，一部分为已访问点，另一部分为未访问点。如果u是割点，那剩下的未被访问点中至少有一个点在不经过点k的情况下无论如何也回不到已访问的点。

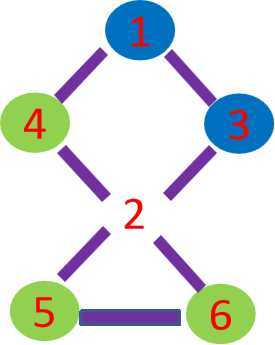
基本思路：

假如到了u后，图中还有顶点v是没有访问过的点，如何判断v在不经过u的情况下是否还能回到之前访问过的任意一个点？u是v的父亲，而之前访问过的顶点就是祖先。 也就是如何检测v在不经过父亲u的情 况下还能否回到祖先。那就是对v再 进行一次dfs，但此次遍历不经过u， 看能否回到祖先。不能u即为割点。

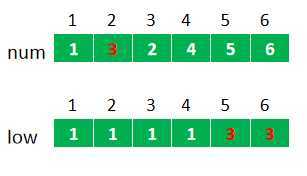
再定义一个数组low来记录每个顶点在不经过父顶点时，能够回到的最小“时间戳”。

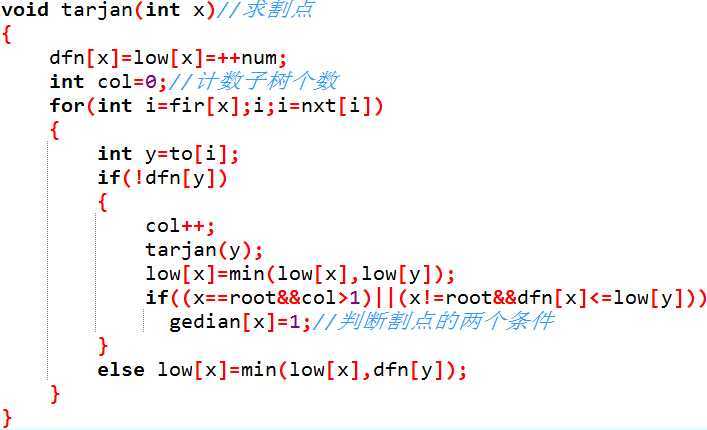
对于某个顶点u，如果存在至少一个顶点v（u的儿子），使得low[v]>=num[u]，即不能回到祖先，那么u点为割点。

 

 

·割边

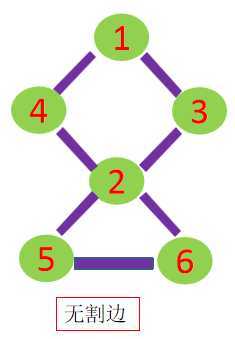
除了割点还有一种问题是求割边（也称桥），即在一个无向图中删除某条边后，图不再连通。

 

 

如何求割边？

只需将求割点的算法修改一个符号就可以。 只需将low[v]>=num[u]改为low[v]>num[u]。

这是为什么呢？

low[v]和num[u]相等则表示还可以回到父亲结点； 而low[v]>num[u]则表示连父亲都回不到了。倘若顶点v不能回到祖先，也没有另外的路能回到父亲，那么 u-v 这条边就是割边。

 

 ·习题

洛谷P3388 【模板】割点（割顶）

一本通习题3.【模板】旅游航道（桥）

--->最近很懒，每天作业很多，所以更题解可能要在碳硫磷考试结束后吧