机房测试11：最小生成树（最小生成树+二分）

Posted 2020-11-16 mowanying

题目：

 

 

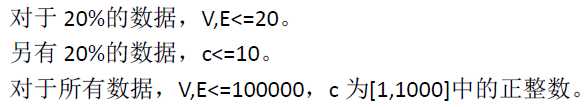
 分析：

如果直接做最小生成树，会出现以下不合法情况：

1.白边选多了。说明白边的权值太小了，我们可以通过加大白边的权值来似的选少一点白边。

2.白边选少了。与上面同理。

我们不知道白边的取值在多少合适，但明显具有单调性（白边权值越大，选的条数一定会减少），所以可以用二分来确定白边的取值。

二分一个取值，将所有白色边权减去mid，做一遍最小生成树，如果能选到>=need条边，就把mid增大。

细节：

1. =need也要把mid增大。

2. 不能只在白边恰好选到need的时候更新答案，这时候很多答案会更新不到

 

#include<bits/stdc++.h>
using namespace std;
#define N 100005
#define ri register int
int read()
{
    int x=0,fl=1; char ch=getchar();
    while(ch<‘0‘||ch>‘9‘) { if(ch==‘-‘) fl=-1; ch=getchar(); }
    while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar();
    return x*fl;
}
int fa[N],ans=1e8+1,n,m,need;
struct node { int a,b,w,col; }tmp[N],e[N];

bool cmp(const node &a,const node &b)
{
    if(a.w==b.w) return a.col<b.col;//在权值相同的情况下记得优先按白边排序 
    return a.w<b.w;
}
int find(int x)
{
    if(x==fa[x]) return fa[x];
    return fa[x]=find(fa[x]);
}
int tot=0;
bool check(int x)
{
    int cnt=0,tot_w=0;
    tot=0;
    for(ri i=1;i<=m;++i) tmp[i]=e[i],tmp[i].w+=x*(tmp[i].col==0);
    sort(tmp+1,tmp+1+m,cmp);
    for(ri i=0;i<=n;++i) fa[i]=i;
    for(ri i=1;i<=m;++i){
        int f1=find(tmp[i].a),f2=find(tmp[i].b);
        if(f1==f2) continue;
        cnt++;
        tot_w+=(tmp[i].col==0); tot+=tmp[i].w;
        fa[f1]=f2; 
        if(cnt==n-1) break;
    }
    //if(tot_w==need) ans=min(ans,tot-need*x);//不能这样写!!!
    //有可能白边选多了 也可以更新答案 因为这时有些白边的权值是==黑边权值的 而我们优先按照白边排了序 多选了白边
    //导致看起来无解 但其实是有解的 只需要把相同权值的白边替换成黑边即可 
    return tot_w>=need;//=也要return true 因为这样可以使ans尽量小 
}
int main()
{
    //freopen("e.in","r",stdin);
    //freopen("e.out","w",stdout);
    n=read(); m=read(); need=read();
    for(ri i=1;i<=m;++i) e[i].a=read(),e[i].b=read(),e[i].w=read(),e[i].col=read();
    int l=-101,r=101;
    while(l<=r){
        int mid=(l+r)/2;//负值 
        //printf("mid:%d
",mid);
        if(check(mid)) l=mid+1,ans=tot-need*mid;//
        else r=mid-1;
    }
    printf("%d
",ans);
}
/*
3 3 1
1 2 100 1
1 3 20 0
2 3 25 0

2 2 1
0 1 1 1
0 1 2 0
*/

View Code