机器学习统计学习

Posted 2021-03-26 colleenhe

统计学习

前言：机器学习比较重要的几部分：线性模型、统计学习、深度学习，线性部分包括SVM、压缩感知、稀疏编码，都是控制整个模型的稀疏性去做线性函数，偏 Discriminative 判别模型；统计学习主要通过统计方法对数据建模找到极大似然，偏 Generative 生成方法；深度学习就是 neural model，偏非线性。

机器学习中的统计多是基于对事件的不确定性度量关于，是主观的，而不是客观地基于频次。

EM算法 ( 期望最大算法，Expectation Maximum )

参考：EM-最大期望算法

隐含变量

给定训练数据 (D={(x^{(1)},y^{(1)}),...,(x^{(N)},y^{(N)})})，一般想学习到的情况是 (x^{(i)}) 和 (y^{(i)}) 之间的函数关系，但是在统计学习里想学习到的是 (P(y^{(i)}|x^{(i)}))，在二分类问题里就是 (P(0|x^{(i)})) 和 (P(1|x^{(i)})=1-P(0|x^{(i)}))。

一般假设数据服从某种分布，根据给定数据估计分布函数的参数，求极大似然值。(L(mu,sigma)=prod_{i=1}^N P(x^{(i)}|mu,sigma)=sum_{i=1}^N logP(x^{(i)}|mu,sigma))

隐含变量和概率分布的关系

变量 (X) 每一个维度都相互独立

[P(X)=P(x_1,x_2,...,x_n)=prod_{j=1}^n P(x_j)]

若 (X) 和某隐含变量 (Z) 相关

[P(X)=sum_ZP(X,Z)边缘概率=sum_ZP(X|Z)P(Z)]

• 已知 (Z) 和 (X) 有某种隐含关系，(P(X|Z)) 是可以求出来的
• (P(Z)) 可假设 (Z) 服从某种先验分布

举例

掷硬币，(X={0,1})，认为掷硬币的结果可能和高度相关，(Z) 为掷硬币的高度，抛掷高度、角度等都是假象的可能和结果有关的变量，我们假想这些因素来刻画数据的肌理，就是所谓 Generative Model。

假设三枚硬币 (A,B,C)，掷出正面的概率分别为 (pi,p,q)，想象生成过程比较复杂，掷出 (A) ，若结果为 1 ，就掷 (B)，若结果为 0 ，就掷 (C)，每次先掷 (A)，由 (A) 的结果决定掷 (B) 还是 (C)，记下 (B,C) 的结果，生成 (Y=(y^{(1)},y^{(2)},...,y^{(N)}))，如何预测 (y^{(i)})。

1. 有参模型，( heta=(pi,p,q))

2. 求 (P(y| heta)=sum_ZP(y,Z| heta))，引入一个隐含变量 (Z)，控制事件 (y)，表示 (A) 硬币的结果，(Z=1) 表示掷的硬币 (B)，(Z=0) 表示掷的硬币 (C)。

   • (P(y| heta)=sum_ZP(y|Z, heta)P(Z| heta))

   • (P(Z| heta)=P(Z|(pi,p,q))=pi)，因为 (P(Z=1| heta)=pi)，(P(Z=0| heta)=1-pi)

   • (sum_ZP(y|Z, heta)=P(y|Z=1, heta)+P(y|Z=0, heta))

     • (P(y|Z=1, heta)=p^y(1-p)^{1-y})

       (P(y|Z=0, heta)=q^y(1-q)^{1-y})

3. 拆开
   [z=1quad P(y| heta)=pi p^y(1-p)^{1-y}z=0 quad P(y| heta)=(1-pi)q^y(1-q)^{1-y}Rightarrow P(y| heta)=pi p^y(1-p)^{1-y}+(1-pi)q^y(1-q)^{1-y}]

4. 似然值为

   [P(Y| heta)=prod_{i=1}^NP(y^{(i)}| heta)=prod_{i=1}^Npi p^{y^{(i)}}(1-p)^{1-y^{(i)}}+(1-pi)q^{y^{(i)}}(1-q)^{1-y^{(i)}}=sum_{i=1}^N log P(y^{(i)}| heta)]

5. 求 (pi,p,q)。只知道 (y^{(i)})，如何估计 (pi,p,q)。

   • (P(y| heta)=pi p^y(1-p)^{1-y}+(1-pi)q^y(1-q)^{1-y}) 是混合模型 ，(p^y(1-p)^{1-y}) 是硬币 (B) 掷出来的伯努利分布，(q^y(1-q)^{1-y}) 是硬币 (C) 结果的伯努利分布。(pi) 和 (1-pi) 就像两个事情的权重，就是两事件的混合模型 (多模态混合，(alpha_1P_1,...,alpha_nP_n)，(sum_ialpha_i=1))。

   • (p=frac{num (B正面)}{N}) ，(q=frac{num (C正面)}{N})，(pi=frac{num (B)}{N})

   • E.step：

     [mu=frac{pi p^y(1-p)^{1-y}}{pi p^y(1-p)^{1-y}+(1-pi)q^y(1-q)^{1-y}}]

     • 给出掷出结果是硬币 (B) 掷出的概率

   • M.step:

     [pi = frac{1}{N}sum_{j=1}^{N} mu_j]

     • 对每一次掷出结果是硬币 (B) 掷出的概率求均值，得出整体来说是硬币 (B) 掷出的概率

     [p=frac{sum_{j=1}^N mu_j y^{(j)}}{sum_{j=1}^N mu_j}]

     • (y^{(j)}=1) 正面，(y^{(j)}=0) 反面

     [q=frac{sum_{j=1}^N (1-mu_j) y^{(j)}}{sum_{j=1}^N (1-mu_j)}]

     • 对 (pi,p,q) 进行最大化估计

6. 由 ( heta_0=(pi_0,p_0,q_0)) 互相迭代至 (pi,p,q) 不再变化，结果就是对 (pi,p,q) 最好的估计

琴生不等式

1. (f) 是凸函数，对任意变量 (x):

   [E(f(x))ge f(E(x))]

2. (f) 是凹函数，对任意变量 (x):

   [E(f(x))le f(E(x))]

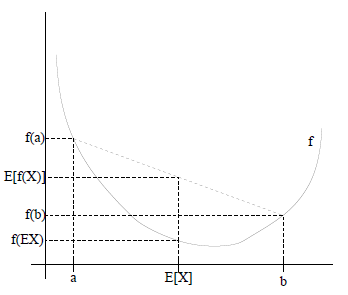
琴生不等式在EM的应用

求极大似然值

[L( heta)=sum_{i=1}^m logP(x| heta)=sum_{i=1}^mlogsum_zP(x,z| heta)]

• (z) 隐含变量

展开

[sum_i logP(x^{(i)}| heta)=sum_ilog sum_{z^{(i)}}P(x^{(i)},z^{(i)}| heta)=sum_ilogsum_{z^{(i)}}Q_i(z^{(i)})frac{P(x^{(i)},z^{(i)}| heta)}{Q_i(z^{(i)})} ge sum_isum_{z^{(i)}}Q_i(z^{(i)})logfrac{P(x^{(i)},z^{(i)}| heta)}{Q_i(z^{(i)})}]

• (E(g(x))=sum_x g(x)P(x))
• (Q_i(z^{(i)})) 表示 (z^{(i)}) 的概率分布 (P(z^{(i)}))
• (sum_{z^{(i)}}Q_i(z^{i})frac{P(x^{(i)},z^{(i)}| heta)}{Q_i(z^{i})}) 可看成函数 (g(z^{(i)})=frac{P(x^{(i)},z^{(i)}| heta)}{Q_i(z^{i})}) 数学期望
• 将 (log) 提出来，因为 (log) 是凹函数，根据琴生不等式 (log(E(x))ge E(log(x)))

要提高极大似然值，就优化下界使最大化。函数 (sum_isum_{z^{(i)}}Q_i(z^{(i)})logfrac{P(x^{(i)},z^{(i)}| heta)}{Q_i(z^{(i)})}) 记作 (E(f(z^{(i)})))，要使得该期望最大化，需满足 (f(z^{(1)})=f(z^{(2)})=...=f(z^{(n)}))，即

[frac{P(x^{(i)},z^{(i)}| heta)}{Q_i(z^{(i)})}=c Leftrightarrow Q_i(z^{(i)}) varpropto P(x^{(i)},z^{(i)}| heta)]

因为 (sum_zQ_i(z^{(i)})=1)，则

[Q_i(z^{(i)}) = frac{P(x^{(i)},z^{(i)}| heta)}{sum_z P(x^{(i)},z^{(i)}| heta)}=frac{P(x^{(i)},z^{(i)}| heta)}{P(x^{(i)}| heta)}=P(z^{(i)}|x^{(i)}, heta)]

EM 算法公式表述

迭代至收敛 {

? (E-step) ，for each (i)，set

(Q_i(z^{(i)}):=P(z^{(i)}|x^{(i)}, heta))

(M-step) ，set

$ heta:= arg ?max_{ heta}sum_isum_{z^{(i)}}Q_i(z^{(i)})logfrac{p(x^{(i)},z^{(i)}| heta)}{Q_i(z^{(i)})}$
}

• EM 算法常用于估计参数隐变量
• EM 算法通过引入隐含变量，使用 MLE (极大似然估计) 进行迭代求解参数。
• E-step 通过已有数据和现有模型估计隐含参数
• M-step 假设隐含参数已知的情况下，最大化似然函数从而获取新的参数值

高斯混合模型 ( Gaussian Mixed Model, GMM)

高斯分布 ( 正态分布 ) 函数：(X sim N(mu,sigma^2))

高斯混合模型就是多个高斯分布函数的线性组合，通常用于处理同一集合数据分布类型不同的情况。

高斯混合模型能够平滑地近似任意形状的密度分布。

二维混合模型

假设第一个高斯分布参数为 (mu_1,sigma_1)，第二个高斯分布参数为 (mu_2,sigma_2)，混合两个高斯分布的模型满足

[P(x| heta)P(x|mu_1,mu_2,delta_1,delta_2,pi)=pi N(mu_1,delta_1)+(1-pi)N(mu_2,delta_2)]

给定数据为 (D={x^{(1)},x^{(2)},...,x^{(N)}})

参数的极大似然值

[L( heta)=arg maxP(D| heta)=arg max prod_{i=0}^N P(x^{(i)}| heta)=arg max sum_{i=1}^N log P(x^{(i)}| heta) ]

如何求 (P(x^{(i)}| heta))

[P(x| heta)=sum_zP(x,z| heta)=sum_z P(x|z, heta)P(z| heta) (由联合概率变为条件概率和其先验分布) =sum P(x|z=0, heta)P(z=0| heta)+P(x|z=1, heta)P(z=1| heta)=pi N(mu_1,delta_1)+(1-pi)N(mu_2,delta_2)]

对观察数据 (x^{(j)}) 推测属于哪个高斯分布函数，概率为

[w^{(j)}=frac{pi cdot P(x^{(j)}|mu_1,delta_1)}{pi cdot P(x^{(j)}|mu_1,delta_1)+(1-pi) cdot P(x^{(j)}|mu_2,delta_2)}]

• 这步是 (E-step)，估计参数

[pi=frac{sum_{j=1}^N w^{(j)}}{N}mu_1=frac{sum_{j=1}^N w^{(j)}x^{(j)}}{sum_{j=1}^Nw^{(j)}}mu_2=frac{sum_{j=1}^N (1-w^{(j)})x^{(j)}}{sum_{j=1}^N(1-w^{(j)})}delta_1^2=frac{w^{(j)}(x^{(j)}-mu_1)^2}{sum_{j=1}^Nw^{(j)}}delta_2^2=frac{(1-w^{(j)})(x^{(j)}-mu_2)^2}{sum_{j=1}^N(1-w^{(j)})}]

• 这是 (M-step)，代入参数估计值

多维混合模型

[p(x)=sum_{k=1}^Kpi_kN(x|mu_k,delta_k)]

• (N(x|mu_k,delta_k)) 称为混合模型中第 (k) 个分量
• (pi_k) 是混合系数，是每个分量的权重，是每个分量被选中的概率
• (sum_{k=1}^Kpi_k=1 (0 le pi_k le 1))

隐马尔可夫模型

高维下的高斯模型

主题模型

Dirichlet 分布