网络流总结
Posted bxd123
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了网络流总结相关的知识,希望对你有一定的参考价值。
最大流

#include<bits/stdc++.h> using namespace std; #define inf 0x3f3f3f3f const int N=1e4+10; const int M=1e5+10; struct Edge { int to, next, w; } edge[M<<1]; int head[N],cur[N],pos=1,level[N]; void add(int a, int b, int c) { edge[++pos] = (Edge){b, head[a], c};head[a] = pos; edge[++pos] = (Edge){a, head[b], 0};head[b] = pos; } bool bfs(int s, int t) { memset(level, 0, sizeof level); queue<int> q; level[s] = 1; q.push(s); while (!q.empty()) { int pos = q.front();q.pop(); for (int i = head[pos]; i; i = edge[i].next) { int v = edge[i].to; if (!edge[i].w || level[v]) continue; level[v] = level[pos] + 1; q.push(v); } } return level[t]; } int dfs(int s, int t, int flow) { if(s==t||flow==0)return flow; int f,ret = 0; for (int &i = cur[s],v; i; i = edge[i].next) { v = edge[i].to; if (level[v] == level[s] + 1 && (f=dfs(v,t,min(flow,edge[i].w)))>0) { edge[i].w -= f; edge[i ^ 1].w += f; flow -= f; ret += f; if(!flow)break; } } return ret; } int dinic(int s, int t) { int ret = 0; while (bfs(s, t)) memcpy(cur,head,sizeof cur),ret += dfs(s, t, inf); return ret; } /* 4 5 4 3 4 2 30 4 3 20 2 3 20 2 1 30 1 3 40 50 */
最小割
两点式模型:主要解决分为两个阵营的选与不选问题 通常是求最大效益 一般用最小割模型
P1361 小M的作物
题意:
有两块耕地A和B 有n种作物 第i种作物种到A地可以获得ai效益 种到B可以获得Bi 还有m对组合
第i个组合中的作物共同种在A中可以获得c1i的额外收益,共同总在B中可以获得c2i的额外收益
题解:
- 显然设置A为S B为T
- 如果没有组合的话非常简单 连S为ai 连T为bi 即可
- 考虑到这种组合是将两种作物强行捆绑在一起 可以建立一个虚点 然后两个种子连虚点inf 虚点连A或B连即可
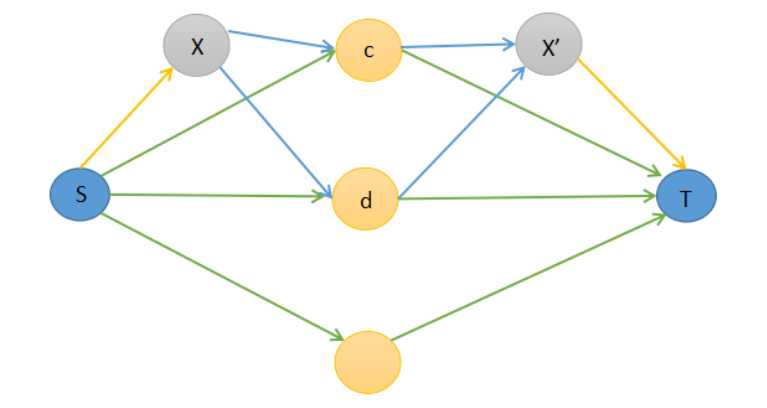
最大权闭合子图: s连项目容量为获利 每个 项目连需求inf 每个需求连t 花费 答案为获利和-最小割
P4177 [CEOI2008]order
题意:
有N个工作,M种机器,每种机器你可以租或者买过来. 每个工作包括若干道工序,每道工序需要某种机器来完成,你可以通过购买或租用机器来完成。 现在给出这些参数,求最大利润。
题解:
- 看题意很容易想到最大权闭合子图 但是这题多了一种租赁器材的方式
- 考虑最大权闭合子图的含义 可以看作与s联通表示选择该实验(所以割去器材花费) 与t联通表示放弃该实验(割去实验利益)
- 注意到实验连器材的边为inf 表示不可割去 这题租赁的含义恰巧就是该边的容量变为租赁费用

#include<bits/stdc++.h> using namespace std; #define inf 0x3f3f3f3f const int N=2400+10; const int M=3e6+10; struct Edge { int to, next, w; } edge[M<<1]; int head[N],cur[N],pos=1,level[N]; void add(int a, int b, int c) { edge[++pos] = (Edge){b, head[a], c};head[a] = pos; edge[++pos] = (Edge){a, head[b], 0};head[b] = pos; } bool bfs(int s, int t) { memset(level, 0, sizeof level); queue<int> q; level[s] = 1; q.push(s); while (!q.empty()) { int pos = q.front();q.pop(); for (int i = head[pos]; i; i = edge[i].next) { int v = edge[i].to; if (!edge[i].w || level[v]) continue; level[v] = level[pos] + 1; q.push(v); } } return level[t]; } int dfs(int s, int t, int flow) { if(s==t||flow==0)return flow; int f,ret = 0; for (int &i = cur[s],v; i; i = edge[i].next) { v = edge[i].to; if (level[v] == level[s] + 1 && (f=dfs(v,t,min(flow,edge[i].w)))>0) { edge[i].w -= f; edge[i ^ 1].w += f; flow -= f; ret += f; if(!flow)break; } } return ret; } int dinic(int s, int t) { int ret = 0; while (bfs(s, t)) memcpy(cur,head,sizeof cur),ret += dfs(s, t, inf); return ret; } int s,t,n,m,sum,x,y,z,q; int main() { cin>>n>>m; s=n+m+1;t=s+1; for(int i=1;i<=n;i++) { scanf("%d%d",&x,&q);sum+=x; add(s,i,x); while(q--) { scanf("%d%d",&x,&y); add(i,x+n,y); } } for(int i=1;i<=m;i++) scanf("%d",&x),add(i+n,t,x); cout<<sum-dinic(s,t); return 0; }
最小费用最大流
P1251 餐巾计划问题
题意:
一个餐厅每天早上需要ai条干净毛巾 每天晚上会得到ai条脏毛巾 购买一条毛巾需要p元 快洗一条毛巾需要n天 每条f元 慢洗一条毛巾需要m天 每条s元 问满足每天需求的最少花费
题解:
我们要处理的东西是脏毛巾 所以可以将晚上看作是入度 得到ai条毛巾(s-入),早上看成是出度 连t 表示完成任务,储存的话每天晚上连到后一天晚上即可(因为储存的显然都是脏毛巾 所以都是晚上) 快洗和慢洗 只要该天晚上连到后面的第n天早上即可。这题没什么技巧 按照题意连即可。

#include< bits/stdc++.h > using namespace std; typedef long long ll; const int N=500000+10,M=5e5+10; const int inf=0x3f3f3f3f; ll maxflow,mincost; int last[N],pre[N],dis[N],flow[N]; bool vis[N]; struct Edge{int next,to,flow,dis;}edge[M<<1]; int pos=1,head[N]; void init(){pos=1;memset(head,0,sizeof head);mincost=maxflow=0;} queue <int> q; void add(int from,int to,int flow,int dis)//flow流量 dis费用 { edge[++pos].next=head[from];edge[pos].flow=flow;edge[pos].dis=dis;edge[pos].to=to;head[from]=pos; edge[++pos].next=head[to];edge[pos].flow=0;edge[pos].dis=-dis;edge[pos].to=from;head[to]=pos; } bool spfa(int s,int t) { memset(dis,0x3f,sizeof dis); memset(flow,0x3f,sizeof flow); memset(vis,0,sizeof vis); while (!q.empty()) q.pop(); dis[s]=0; pre[t]=-1; q.push(s); vis[s]=1; int tot=0; while (!q.empty()) { int now=q.front(); q.pop(); vis[now]=0; for (int i=head[now]; i; i=edge[i].next) { int to=edge[i].to; if (edge[i].flow>0 && dis[to]>dis[now]+edge[i].dis) { dis[to]=edge[i].dis+dis[now]; flow[to]=min(edge[i].flow,flow[now]); last[to]=i; pre[to]=now; if (!vis[to]) { q.push(to); vis[to]=1; } } } } return pre[t]!=-1; } void MCMF(int s,int t) { while (spfa(s,t)) { int now=t; maxflow+=flow[t]; mincost+=flow[t]*dis[t]; while (now!=s) { edge[last[now]].flow-=flow[t];//dis . flow edge[last[now]^1].flow+=flow[t]; now=pre[now]; } } } int n,m,S,T,p,f,s,NN,x,a[N]; int main() { cin>>NN; S=2*NN+1;T=S+1; for(int i=1;i<=NN;i++)scanf("%d",&a[i]),add(S,i+NN,a[i],0),add(i,T,a[i],0); cin>>p>>m>>f>>n>>s; for(int i=1;i<=NN;i++) { add(S,i,inf,p); if(i+1<=NN)add(i+NN,i+NN+1,inf,0); if(i+m<=NN)add(i+NN,i+m,inf,f); if(i+n<=NN)add(i+NN,i+n,inf,s); } MCMF(S,T); cout<< mincost; return 0; }
上下界网络流
以上是关于网络流总结的主要内容,如果未能解决你的问题,请参考以下文章
