[分治算法]骨牌铺方格

Posted 2021-03-26 onetrainee

骨牌铺方格

Time Limit: 1000 ms Memory Limit: 32768 KiB

 

Problem Description

在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格，骨牌的铺放方案有三种,如下图：

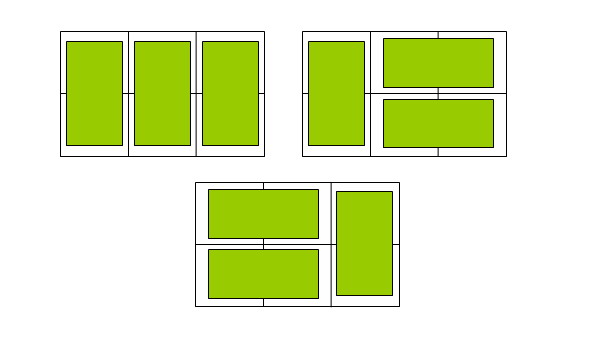
Input

输入数据由多行组成，每行包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0< n<=50)。

Output

对于每个测试实例，请输出铺放方案的总数，每个实例的输出占一行。

Sample Input

1
3
2

Sample Output

1
3
2

---

算法思路：
分治算法核心就是缩小问题规模，一般有两种缩小思路：二分法/递减法，显然这个问题采用"递减法"比较好。

 

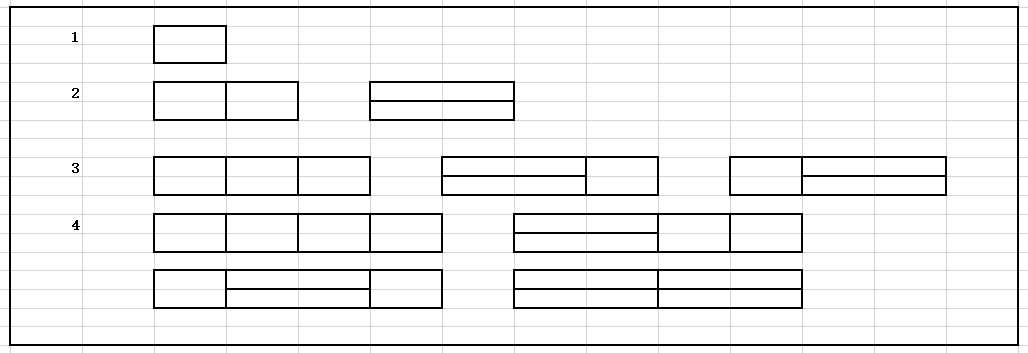
推算如上图，现在假设需要计算第N个，即把N-1时再添加"一个竖着的情况"(因为第N-1个我们把各种情况计算出来了，所以无需操心)；但是我们缺少横着的情况，那么再往前推N-2个，再添加一个"横着的情况"。

因此得到递推算法 func(n)=func(n-1)+func(n-2)。

至于放在左右问题，因为之前N-1与N-2满足所有情况，左右无关紧要，算作一种（对称）。

 

源代码：

 

 1 // 算法.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
 2 //
 3 
 4 #include "pch.h"
 5 #include <iostream>
 6 #include <map>
 7 #include <math.h>
 8 #include <algorithm>
 9 using namespace std;
10 
11 
12 int main() {
13 
14     long long int num[51];
15     int n;
16     int count = 0;
17     while (~scanf_s("%d",&n)) {
18         count = 0;
19         num[1] = 1;
20         num[2] = 2;
21         for (int i = 3; i <= n; i++) {
22             num[i] = num[i - 1] + num[i - 2];
23         }
24         printf("%lld
", num[n]);
25     }
26 }