Pytorch+PyG实现GCN(图卷积网络)

Posted 2023-04-02 海洋.之心

文章目录

• 前言
• 一、导入相关库
• 二、加载Cora数据集
• 三、定义GCN网络
• 四、定义模型
• 五、模型训练
• 六、模型验证
• 七、结果
• 完整代码

---

前言

大家好，我是阿光。

本专栏整理了《图神经网络代码实战》，内包含了不同图神经网络的相关代码实现（PyG以及自实现），理论与实践相结合，如GCN、GAT、GraphSAGE等经典图网络，每一个代码实例都附带有完整的代码。

正在更新中~ ✨

🚨 我的项目环境：

• 平台：Windows10
• 语言环境：python3.7
• 编译器：PyCharm
• PyTorch版本：1.11.0
• PyG版本：2.1.0

💥 项目专栏：【图神经网络代码实战目录】

---

本文我们将使用Pytorch + Pytorch Geometric来简易实现一个GCN（图卷积网络），让新手可以理解如何PyG来搭建一个简易的图网络实例demo。

一、导入相关库

本项目我们需要结合两个库，一个是Pytorch，因为还需要按照torch的网络搭建模型进行书写，第二个是PyG，因为在torch中并没有关于图网络层的定义，所以需要torch_geometric这个库来定义一些图层。

import torch
import torch.nn.functional as F
import torch.nn as nn
import torch_geometric.nn as pyg_nn
from torch_geometric.datasets import Planetoid

二、加载Cora数据集

本文使用的数据集是比较经典的Cora数据集，它是一个根据科学论文之间相互引用关系而构建的Graph数据集合，论文分为7类，共2708篇。

• Genetic_Algorithms
• Neural_Networks
• Probabilistic_Methods
• Reinforcement_Learning
• Rule_Learning
• Theory

这个数据集是一个用于图节点分类的任务，数据集中只有一张图，这张图中含有2708个节点，10556条边，每个节点的特征维度为1433。

# 1.加载Cora数据集
dataset = Planetoid(root='./data/Cora', name='Cora')

三、定义GCN网络

这里我们就不重点介绍GCN网络了，相信大家能够掌握基本原理，本文我们使用的是PyG定义网络层，在PyG中已经定义好了GCNConv这个层，该层采用的就是GCN机制。

对于GCNConv的常用参数：

• in_channels：每个样本的输入维度，就是每个节点的特征维度
• out_channels：经过注意力机制后映射成的新的维度，就是经过GAT后每个节点的维度长度
• normalize：是否添加自环，并且是否归一化，默认为True
• add_self_loops：为图添加自环，是否考虑自身节点的信息
• bias：训练一个偏置b

# 2.定义GCNConv网络
class GCN(nn.Module):
    def __init__(self, num_node_features, num_classes):
        super(GCN, self).__init__()
        self.conv1 = pyg_nn.GCNConv(num_node_features, 16)
        self.conv2 = pyg_nn.GCNConv(16, num_classes)
        
    def forward(self, data):
        x, edge_index = data.x, data.edge_index
        
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)
        
        return F.log_softmax(x, dim=1)

上面网络我们定义了两个GCNConv层，第一层的参数的输入维度就是初始每个节点的特征维度，输出维度是16。

第二个层的输入维度为16，输出维度为分类个数，因为我们需要对每个节点进行分类，最终加上softmax操作。

四、定义模型

下面就是定义了一些模型需要的参数，像学习率、迭代次数这些超参数，然后是模型的定义以及优化器及损失函数的定义，和pytorch定义网络是一样的。

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # 设备
epochs = 10 # 学习轮数
lr = 0.003 # 学习率
num_node_features = dataset.num_node_features # 每个节点的特征数
num_classes = dataset.num_classes # 每个节点的类别数
data = dataset[0].to(device) # Cora的一张图

# 3.定义模型
model = GCN(num_node_features, num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=lr) # 优化器
loss_function = nn.NLLLoss() # 损失函数

五、模型训练

模型训练部分也是和pytorch定义网络一样，因为都是需要经过前向传播、反向传播这些过程，对于损失、精度这些指标可以自己添加。

# 训练模式
model.train()

for epoch in range(epochs):
    optimizer.zero_grad()
    pred = model(data)
    
    loss = loss_function(pred[data.train_mask], data.y[data.train_mask]) # 损失
    correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item() # epoch正确分类数目
    acc_train = correct_count_train / data.train_mask.sum().item() # epoch训练精度
    
    loss.backward()
    optimizer.step()
    
    if epoch % 20 == 0:
        print("【EPOCH: 】%s" % str(epoch + 1))
        print('训练损失为：:.4f'.format(loss.item()), '训练精度为：:.4f'.format(acc_train))

print('【Finished Training！】')

六、模型验证

下面就是模型验证阶段，在训练时我们是只使用了训练集，测试的时候我们使用的是测试集，注意这和传统网络测试不太一样，在图像分类一些经典任务中，我们是把数据集分成了两份，分别是训练集、测试集，但是在Cora这个数据集中并没有这样，它区分训练集还是测试集使用的是掩码机制，就是定义了一个和节点长度相同纬度的数组，该数组的每个位置为True或者False，标记着是否使用该节点的数据进行训练。

# 模型验证
model.eval()
pred = model(data)

# 训练集（使用了掩码）
correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item()
acc_train = correct_count_train / data.train_mask.sum().item()
loss_train = loss_function(pred[data.train_mask], data.y[data.train_mask]).item()

# 测试集
correct_count_test = pred.argmax(axis=1)[data.test_mask].eq(data.y[data.test_mask]).sum().item()
acc_test = correct_count_test / data.test_mask.sum().item()
loss_test = loss_function(pred[data.test_mask], data.y[data.test_mask]).item()

print('Train Accuracy: :.4f'.format(acc_train), 'Train Loss: :.4f'.format(loss_train))
print('Test  Accuracy: :.4f'.format(acc_test), 'Test  Loss: :.4f'.format(loss_test))

七、结果

【EPOCH: 】1
训练损失为：1.9594 训练精度为：0.1571
【EPOCH: 】21
训练损失为：1.8681 训练精度为：0.3286
【EPOCH: 】41
训练损失为：1.7647 训练精度为：0.5000
【EPOCH: 】61
训练损失为：1.6587 训练精度为：0.5571
【EPOCH: 】81
训练损失为：1.5258 训练精度为：0.6714
【EPOCH: 】101
训练损失为：1.4334 训练精度为：0.7143
【EPOCH: 】121
训练损失为：1.3361 训练精度为：0.7714
【EPOCH: 】141
训练损失为：1.2310 训练精度为：0.8357
【EPOCH: 】161
训练损失为：1.1443 训练精度为：0.8571
【EPOCH: 】181
训练损失为：1.0962 训练精度为：0.8714
【Finished Training！】

>>>Train Accuracy: 0.9357 Train Loss: 0.9735
>>>Test  Accuracy: 0.7200 Test  Loss: 1.3561

	训练集	测试集
Accuracy	0.9357	0.7200
Loss	0.9735	1.3561

完整代码

import torch
import torch.nn.functional as F
import torch.nn as nn
import torch_geometric.nn as pyg_nn
from torch_geometric.datasets import Planetoid

# 1.加载Cora数据集
dataset = Planetoid(root='./data/Cora', name='Cora')

# 2.定义GCNConv网络
class GCN(nn.Module):
    def __init__(self, num_node_features, num_classes):
        super(GCN, self).__init__()
        self.conv1 = pyg_nn.GCNConv(num_node_features, 16)
        self.conv2 = pyg_nn.GCNConv(16, num_classes)
        
    def forward(self, data):
        x, edge_index = data.x, data.edge_index
        
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)
        
        return F.log_softmax(x, dim=1)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') # 设备
epochs = 200 # 学习轮数
lr = 0.0003 # 学习率
num_node_features = dataset.num_node_features # 每个节点的特征数
num_classes = dataset.num_classes # 每个节点的类别数
data = dataset[0].to(device) # Cora的一张图

# 3.定义模型
model = GCN(num_node_features, num_classes).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=lr) # 优化器
loss_function = nn.NLLLoss() # 损失函数

# 训练模式
model.train()

for epoch in range(epochs):
    optimizer.zero_grad()
    pred = model(data)
    
    loss = loss_function(pred[data.train_mask], data.y[data.train_mask]) # 损失
    correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item() # epoch正确分类数目
    acc_train = correct_count_train / data.train_mask.sum().item() # epoch训练精度
    
    loss.backward()
    optimizer.step()
    
    if epoch % 20 == 0:
        print("【EPOCH: 】%s" % str(epoch + 1))
        print('训练损失为：:.4f'.format(loss.item()), '训练精度为：:.4f'.format(acc_train))

print('【Finished Training！】')

# 模型验证
model.eval()
pred = model(data)

# 训练集（使用了掩码）
correct_count_train = pred.argmax(axis=1)[data.train_mask].eq(data.y[data.train_mask]).sum().item()
acc_train = correct_count_train / data.train_mask.sum().item()
loss_train = loss_function(pred[data.train_mask], data.y[data.train_mask]).item()

# 测试集
correct_count_test = pred.argmax(axis=1)[data.test_mask].eq(data.y[data.test_mask]).sum().item()
acc_test = correct_count_test / data.test_mask.sum().item()
loss_test = loss_function(pred[data.test_mask], data.y[data.test_mask]).item()

print('Train Accuracy: :.4f'.format(acc_train), 'Train Loss: :.4f'.format(loss_train))
print('Test  Accuracy: :.4f'.format(acc_test), 'Test  Loss: :.4f'.format(loss_test))

图卷积神经网络(GCN)综述与实现（PyTorch版)

图卷积神经网络(GCN)综述与实现（PyTorch版)

---

本文的实验环境为PyTorch = 1.11.0 + cu113，PyG = 2.0.4，相关依赖库和数据集的下载请见链接。

---

一、图卷积神经网络介绍

1.1 传统图像卷积

卷积神经网络中的卷积(Convolution)指的是在图像上进行的输入和卷积核之间离散内积运算，其本质上就是利用共享参数的滤波器，通过计算中心值以及相邻节点的值进行加权获得带有局部空间特征的特征提取器。

其具有三个重要的特征，分别为：

• 稀疏连接
  • 相较于全连接层，卷积层输入和输出间的连接是稀疏的，能够大大减少参数的数量，加快网络的训练速度。
• 参数共享
  • 卷积核的权重参数可以被多个函数或操作共享，这样只需要训练一个参数集，而不需要对每个位置都训练一个参数集。此外，由于卷积核的大小一般是小于输入大小，也能起到减少参数数量的作用
• 等变表示
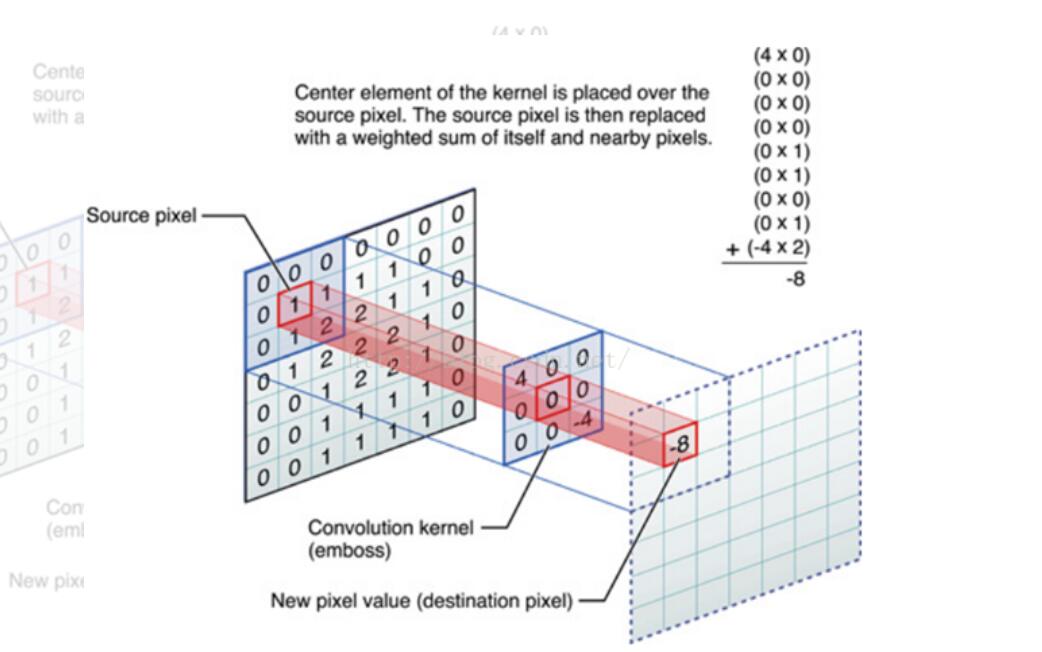
  • 事实上，每个卷积层可以通过多个卷积核来进行特征提取，并且在卷积运算后，卷积神经网络对输入的图像具有平移不变性(有严格的数学论证)
    

一般在卷积层后，会通过一个池化层进行降维，进一步降低网络的复杂度和非线性程度。在那之后，可以将通过卷积池化层后的特征输入全连接层或反卷积层进行进一步的分类、分割、重建工作。当然，传统的卷积操作一般适用于结构化数据。

1.2 图结构

图作为一种典型的非结构化非线性数据(非欧几里得数据)，其可以表示一对一、一对多、多对多的关系，因而常被用于描述复杂的数据对象，譬如社交网络、知识图谱、城市路网、3D点云等。与结构化数据不同，图的局部输入维度可变，即每个节点的邻居节点数量不同；图具有无序性，即节点间并不存在先后关系，仅存在连接关系(点云是置换不变性，在无序性的基础上，交换两点或多点不会影响整体结果)。由于图结构的特殊性，传统CNN和RNN对其的表征能力并不理想。

对于图结构，我们可以将其抽象表示为：
$$G=(V,E)$$
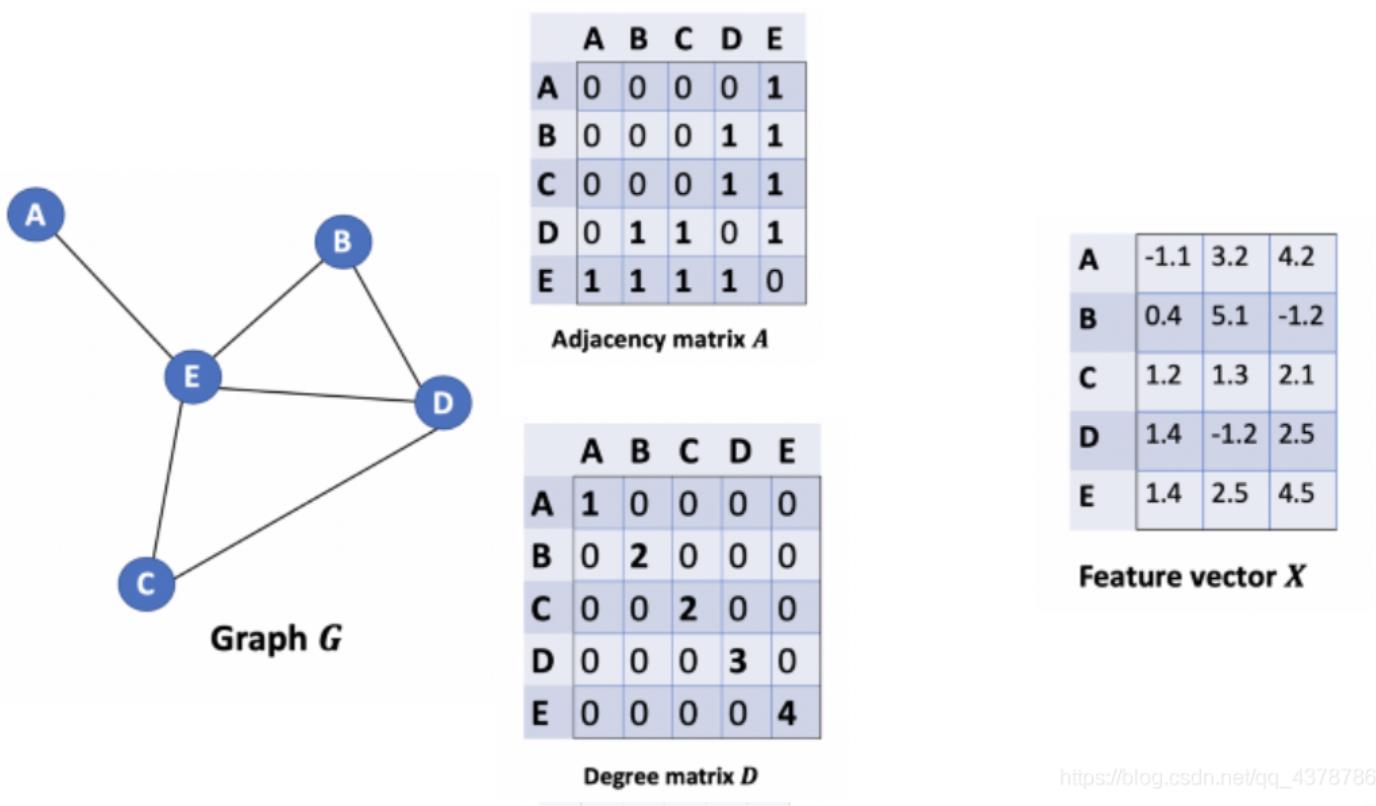
在这里$V$表示图中节点的集合，而$E$为边的集合。对于图特征，我们一般有三个重要矩阵进行表示。

• 邻接矩阵$A$：adjacency matrix用来表示节点间的连接关系。
  

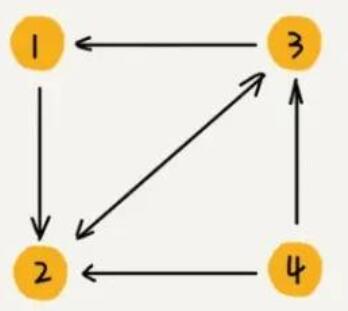
$$\left|\begin{array}{cccccc}& 0& 1& 0& 0& \\ & 0& 0& 1& 0& \\ & 1& 1& 0& 0& \\ & 0& 1& 1& 0& \end{array}\right|$$
​ 对于带权的图，邻接矩阵将把1替换为对应的权重

• 度矩阵$D$：degree matrix用来表示节点的连接数，可以表征某个节点在图中的重要程度，是一个对角矩阵，例如针对上图的入度矩阵：
  $$\left|\begin{array}{cccccc}& 1& 0& 0& 0& \\ & 0& 3& 0& 0& \\ & 0& 0& 2& 0& \\ & 0& 0& 0& 0& \end{array}\right|$$

• 特征矩阵$X$：feature matrix用来表示节点的特征

1.3 图卷积神经网络

目前主流的图卷积基本上可以分为两类，一种是基于谱的图卷积，一种是基于空域的图卷积。

基于谱的图卷积通过傅里叶变换(FFT干的一件事情就是连接空域和频域)将节点映射到频域空间，通过频域空间上的卷积来实现时域上的卷积，最后将特征映射回空域。而基于空域的图卷积则是直接基于节点与邻居进行卷积提取特征，没有做域上的变换。

图卷积算子可表示为：
$$h_i^{l+1}=\sigma (\sum _{j\in N_i}\frac{1}{C_{ij}}{h}_j^l{w}_{R_j}^l)$$
其中，设中心结点为$i$；$h_i^l$为结点$i$在$l$层的特征表达；$\sigma$是非线性激活函数；$C_{ij}$则是归一化因子，譬如结点度的倒数、反距离权重、高斯衰减权重等；$N_i$是结点$i$的邻接节点(包括自身)；$R_i$表示节点$i$的类型；$W_{R_j}$表示$R_j$类型的节点变换权重参数。

---

下面围绕Semi-supervised Classification with Graph Convolutional Networks一文中提出的GCN结构进行分析。

该篇文章由阿姆斯特丹(the University of Amsterdam)大学机器学习专业的Thomas Kipf 博士于2016年提出，并于2017年被深度学习的顶会ICLR(International Conference on Learning Representations)接收！这位大佬的研究方向是学习结构化数据和结构化表示/计算，包括推理、(多智能体)强化学习和结构化深度生成模型。

核心思想

该篇文章提出了一种新的网络结构，用于处理非结构化的图数据，并解决了在一个图中，只有少部分节点的标签是已知情况下的节点分类问题(半监督学习)。

对于带有特征的图结构，例如下图中的$n\times 3$网络结构，有部分是带有标识的，而有部分则是无标识的。

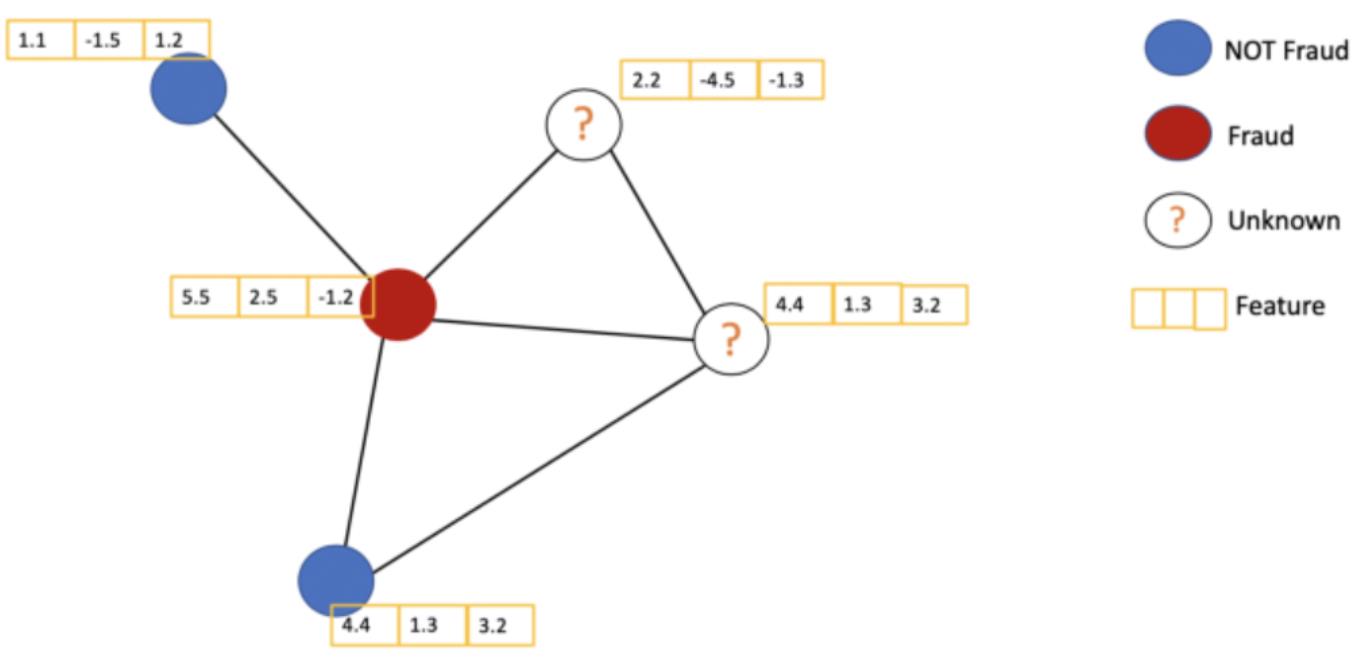
GCN通过考虑节点本身以及邻居节点的特征信息来提取潜在的关系。比如我们在中心节点拼接了邻居的特征后，使用平均池化的方式对这些特征进行聚合，再通过浅层网络进行学习训练得到新的数据。

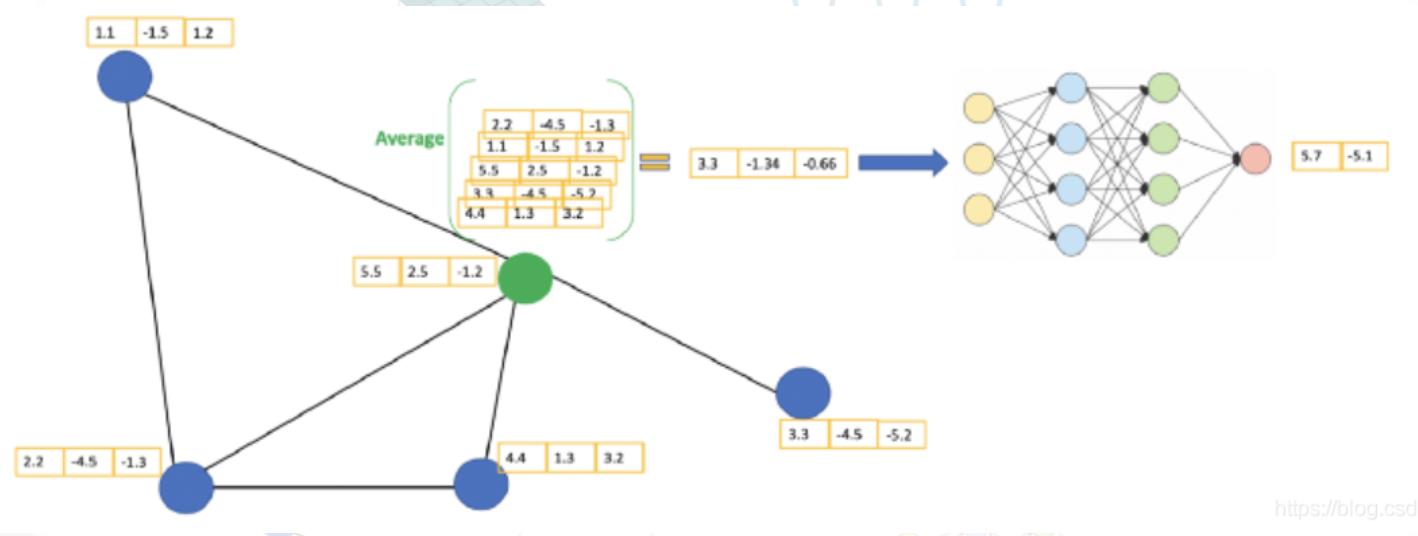
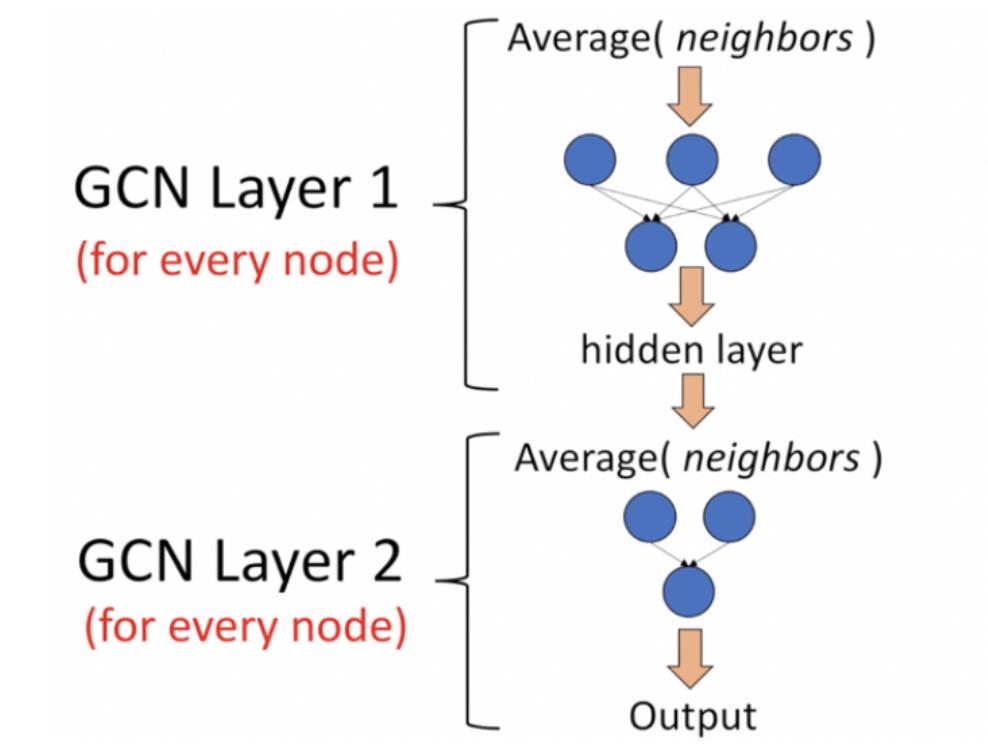
每个GCN层做的事情：

• 获取当前节点和邻接节点特征
• 通过聚合函数获取局部特征(带有拓扑关系)
• 浅层学习训练，获取高维特征
  

数学推导

对于一个如上图所示的无向图，我们要怎么样才能获取到某个节点以及其邻居节点的特征呢？一种非常直观的想法💡是，在当前节点的特征之后，根据权重拼接与之相邻节点的特征。此时，空域上的距离往往成为了权重的影响因素。

那么，邻接表就成了我们考虑节点间拓扑关系最重要的结构。我们写成$A\times X\times W$，$A$是邻接矩阵，$X$是特征矩阵，$W$是权重。右乘相当于控制行，左乘相当于控制列，$A$左乘$X$，相当于在对应节点处，使用哪些节点特征构建新的特征：
$$|\begin{array}{ccccc}& 0& 1& 0& 0\\ & 0& 0& 1& 1\\ & 0& 1& 0& 1\\ & 1& 1& 0& 以上是关于Pytorch+PyG实现GCN(图卷积网络)的主要内容，如果未能解决你的问题，请参考以下文章\end{array}$$

基础GCN图卷积层的pytorch的三种实现。

GCN-图卷积神经网络算法简单实现（含python代码）

深度学习100例 | 第52天-图卷积神经网络（GCN）：实现论文分类

GCN图卷积网络入门详解

深度学习100例 | 第52天-图卷积神经网络（GCN）：实现论文分类

图卷积网络GCN