动态规划-编辑距离

Posted 2021-03-25 mtstory

 

设A和B是2个字符串。要用最少的字符操作将字符串A转换为字符串B。这里所说的字符操作包括 (1)删除一个字符； (2)插入一个字符； (3)将一个字符改为另一个字符。 将字符串A变换为字符串B所用的最少字符操作数称为字符串A到 B的编辑距离，记为d(A,B)。 对于给定的字符串A和字符串B，计算其编辑距离 d(A,B)。

输入格式:

第一行是字符串A，文件的第二行是字符串B。

提示：字符串长度不超过2000个字符。

输出格式:

输出编辑距离d(A,B)

输入样例:

在这里给出一组输入。例如：

fxpimu
xwrs 

输出样例:

在这里给出相应的输出。例如：

5

假设序列S和T的长度分别为m和n, 两者的编辑距离表示为dp[m][n]. 则对序列进行操作时存在以下几种情况:

a, 当S和T的末尾字符相等时, 对末尾字符不需要进行上述定义操作中(亦即"编辑")的任何一个, 也就是不需要增加计数. 则满足条件: dp[m][n] = dp[m - 1][n - 1].

b, 当S和T的末尾字符不相等时, 则需要对两者之一的末尾进行编辑, 相应的计数会增加1.

b1, 对S或T的末尾进行修改, 以使之与T或S相等, 则此时dp[m][n] = dp[m - 1][n - 1] + 1;

b2, 删除S末尾的元素, 使S与T相等, 则此时dp[m][n] = dp[m - 1][n] + 1;

b3, 删除T末尾的元素, 使T与S相等, 则此时dp[m][n] = dp[m][n - 1] + 1;

b4, 在S的末尾添加T的尾元素, 使S和T相等, 则此时S的长度变为m+1, 但是此时S和T的末尾元素已经相等, 只需要比较S的前m个元素与T的前n-1个元素, 所以满足dp[m][n] = dp[m][n - 1] + 1;

b5, 在T的末尾添加S的尾元素, 使T和S相等, 此时的情况跟b4相同, 满足dp[m][n] = dp[m - 1][n] + 1;

c, 比较特殊的情况是, 当S为空时, dp[0][n] = n; 而当T为空时, dp[m][0] = m; 这个很好理解, 例如对于序列""和"abc", 则两者的最少操作为3, 即序列""进行3次插入操作, 或者序列"abc"进行3次删除操作.

所以, 以上我们不难推出编辑距离的动态规划方程为:

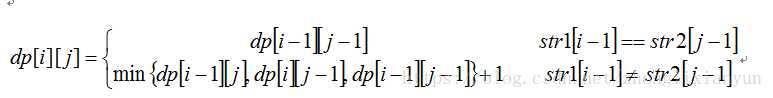
#include<iostream>
using namespace std;
int d[2001][2001];
int main()
{
    int n,m,i,j,k;
    string a,b;
    while(cin>>a>>b)
    {
        n=a.length();
        m=b.length();
        for(i=0;i<=n;i++)
            d[i][0]=i;
        for(j=0;j<=m;j++)
            d[0][j]=j;
        for(i=1;i<=n;i++)
            for(j=1;j<=m;j++)
            {
                k=min(d[i-1][j]+1,d[i][j-1]+1);
                if(a[i-1]!=b[j-1])d[i][j]=min(k,d[i-1][j-1]+1);
                else d[i][j]=min(k,d[i-1][j-1]);
            }
        cout<<d[n][m]<<‘
‘;
    }
    return 0;
}