AI - 过拟合 overfitting

Posted 2021-03-25 yousoluck

Reference

1. How to prevent the overfitting
2. What is the overfitting

Overfitting definition

1. Diagram
   1. 
   2. 
       
       
      　　

The reason of the overfiting

1. The data is limited
2. Model is too complicated

How to avoid the overfitting

1. Argument data
1. Increase the data during the training
2. Argument the data
1. For example: 在物体分类（object recognition）问题中，数据扩增已经成为一项特殊的有效的技术。物体在图像中的位置、姿态、尺度，整体图片敏感度等都不会影响分类结果，所以我们就可以通过图像平移、翻转、缩放、切割等手段将数据库成倍扩充。或者在语音识别（speech recognition）中，加入噪音也被看做是一种数据扩增方式。
2. Enhance the model
   1. 奥卡姆剃刀原则，鼓励简单模型。（过拟合的模型往往是复杂的）

1. 1. Dropout： 就是让神经网络在前向传播的时候，让某个神经元的激活值以一定的概率P，让他停止工作，也就是将这个神经元的激活值变为0。Dropout是非常有效的减少过拟合的方法，通俗的讲当我们挡住了数据的一部分，模型仍然能判断出数据是什么的话，说明模型的能力已经很强。同时挡住了一部分特征，能让模型不依赖于数据的某些局部特征，因为他可能已经被罢工了。
      1. 
   2. Early stopping
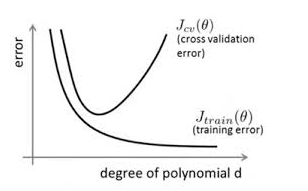
      1. 如下图所示，在对模型训练的时候，模型在训练集上的训练误差(training error)随着时间会一直减少，然而模型在验证集上的验证误差会减少到一定程度后逐步上升，形成一个非对称的U型曲线。对模型进行训练的过程即是对模型的参数进行更新的过程，参数更新会用到一些优化算法，为了能够得到最低测试误差时的参数，Early Stopping的做法就是运行优化方法直到若干次在验证集上的验证误差没有提升时候停止。

         

   3. 正则化 regularization

      1.  正则化（regularization）

         损失函数分为经验风险损失函数和结构风险损失函数，结构风险损失函数就是经验损失函数+表示模型复杂度的正则化，正则项通常选择L1或者L2正则化。结构风险损失函数能够有效地防止过拟合。

         L1正则化是指权值向量中各个元素的绝对值之和，通常表示为，L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择，一定程度上，L1也可以反之过拟合  L2化是指权值向量中各个元素的平方和的平方，通常表示为，L2正则化可以防止模型过拟合 那L1和L2正则化是如何防止过拟合呢？首先我们先明白稀疏参数和更小参数的好处。

         稀疏参数（L1）：参数的稀疏，在一定程度实现了特征的选择。稀疏矩阵指有很多元素为0，少数参数为非零值。一般而言，只有少部分特征对模型有贡献，大部分特征对模型没有贡献或者贡献很小，稀疏参数的引入，使得一些特征对应的参数是0，所以就可以剔除可以将那些没有用的特征，从而实现特征选择。

         更小参数（L2）：越复杂的模型，越是尝试对所有样本进行拟合，那么就会造成在较小的区间中产生较大的波动，这个较大的波动反映出在这个区间内的导数就越大。只有越大的参数才可能产生较大的导数。试想一下，参数大的模型，数据只要偏移一点点，就会对结果造成很大的影响，但是如果参数比较小，数据的偏移对结果的影响力就不会有什么影响，那么模型也就能够适应不同的数据集，也就是泛化能力强，所以一定程度上避免过拟合。2.2  正则化（regularization）

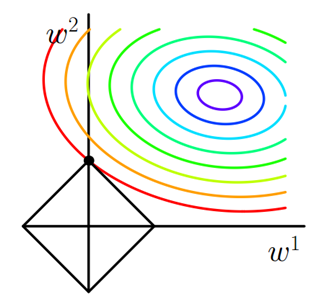
         假设带有L1正则化的损失函数为：，当我们在后添加L1正则化项时，相当于对做了一个约束。此时我们的任务就变成在L1正则化约束下求出取最小值的解。考虑二维的情况，在有两个权值和的情况下，此时L1为，对于梯度下降方法，求解的过程用等值线表示，如下图所示。黑色方形是L1正则化的图形，五彩斑斓的等值线是的等值线。在图中，等值线与黑色方形首次相交的地方就是最优解。因为黑色方形棱角分明（二维情况下四个，多维情况下更多），与这些棱角接触的几率要远大于其他部位接触的概率，而在这些棱角上，会有很多权值为0，这就是为什么L1正则化可以产生稀疏模型，进而可以用于特征选择。

         L1正则化

          

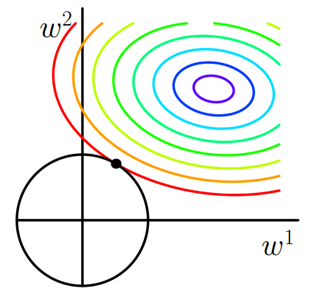
         假设带有L2正则化的损失函数为：，类似地，可以得到下图在二维平面上的图形。因为二维L2正则化函数是个圆，与L1的方形相比，圆滑了好多，因此和L2相交于棱角的几率比较小，而是更多权值取值更小。

         1.  

            　　 

   4. 集成学习：简而言之，训练多个模型，以每个模型的平均输出作为结果。