数字图像处理 灰度共生矩阵特征分析法

Posted 2021-03-25 -wenli

 

灰度共生矩阵特征分析法

相邻某一间隔长度的两个像素，它们之间要么具有相同的灰度级，要么具有不同的灰度级，若能找出这样两个像素的联合分布的统计形式，对于图像的纹理分析很有意义。

灰度共生矩阵(GLDM)的统计方法是20世纪70年代初由R.Haralick等人提出的，它是在假定图像中各像素间的空间分布关系包含了图像纹理信息的前提下，提出的具有广泛性的纹理分析方法。

灰度共生矩阵被定义为从图像中每一个灰度为i的像素点出发，离开某个固定位置（相隔距离为d，方位为0度、45度、90度等），正好灰度值为j的概率，即所有估计的值可以表示成一个矩阵的形式，以此被称为灰度共生矩阵。
这里：

• 1.从哪个灰度级i出发，人为指定。
• 2.相隔距离与方向也人为指定,方向可以通过[0 d]来指定。

1. 0度：              [0 d]
2. 45度：             [-d d]
3. 90度：             [-d 0]
4. 135度：            [-d -d]

• 3.另一个灰度级j也人为指定。

对于纹理变化缓慢的图像，其灰度共生矩阵对角线上的数值较大；而对于纹理变化较快的图像，其灰度共生矩阵对角线上的数值较小，对角线两侧的值较大。
由于灰度共生矩阵的数据量较大，一般不直接作为区分纹理的特征，而是基于它构建的一些统计量作为纹理分类特征。
Haralick曾提出了14种基于灰度共生矩阵计算出来的统计量：即：能量、熵、对比度、均匀性、相关性、方差、和平均、和方差、和熵、差方差、差平均、差熵、相关信息测度以及最大相关系数。

 

下面：https://www.cnblogs.com/8335IT/p/5648445.html

 

 

 

 

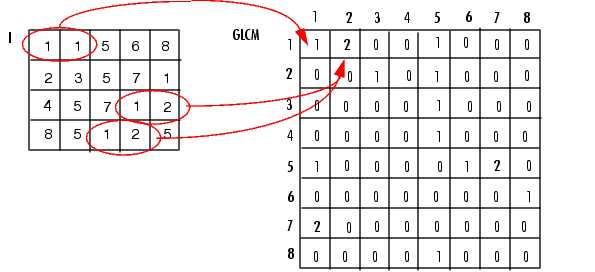
下图显示了如何求解灰度共生矩阵：

下面这幅图总有8个灰度级

以出发点灰度级1，目标点灰度级也为1为例，设查找方向水平间隔为1（方向为水平方向，包括左右），GLCM（1，1）值为1说明只有1对的像素水平相邻。

以出发点灰度级1，目标点灰度级也为2为例，设查找方向水平间隔为1（方向为水平方向，包括左右），GLCM（1，2）值为1说明只有2对的像素水平相邻。

 

 

 

举例几种常用的统计值

1.角二阶矩（Angular Second Moment, ASM)

角二阶矩又称能量，是图像灰度分布均匀程度和纹理粗细的一个度量，反映了图像灰度分布均匀程度和纹理粗细度。当图像纹理均一规则时，能量值较大；反之灰度共生矩阵的元素值相近，能量值较小。

 

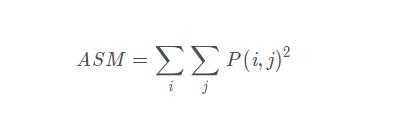
2.熵（Entropy, ENT)

熵度量了图像包含信息量的随机性，表现了图像的复杂程度。当共生矩阵中所有值均相等或者像素值表现出最大的随机性时，熵最大。

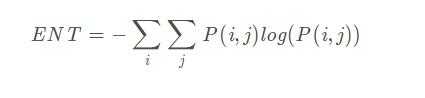
3.对比度

对比度反应了图像的清晰度和纹理的沟纹深浅。纹理越清晰反差越大对比度也就越大。

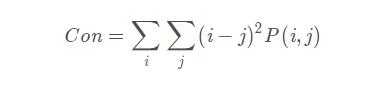
4.反差分矩阵（Inverse Differential Moment, IDM)

反差分矩阵又称逆方差，反映了纹理的清晰程度和规则程度，纹理清晰、规律性较强、易于描述的，值较大。

?

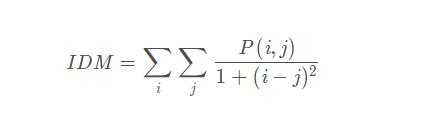
5.能量
能量变换反映了图像灰度分布均匀程度和纹理粗细度。若灰度共生矩阵的元素值相近，则能量较小，表示纹理细致；若其中一些值大，而其它值小，则能量值较大。能量值大表明一种较均一和规则变化的纹理模式。

 

 

 

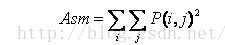
6.逆方差
逆方差反映了图像纹理局部变化的大小，若图像纹理的不同区域间较均匀，变化缓慢，逆方差会较大，反之较小。

 

 

 

7.相关性
用来度量图像的灰度级在行或列方向上的相似程度，因此值得大小反应了局部灰度相关性，值越大，相关性也越大。

 

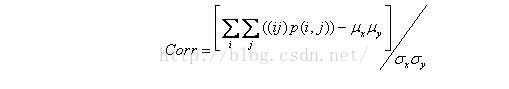
图片来源：https://blog.csdn.net/guanyuqiu/article/details/53117507