HOJ-Contest194-Problem-D 树链剖分

Posted 2021-03-25 golden-elf

题意概述：
      现给出一棵N个结点的树，每个结点可能存在两种状态：0/1，所有结点的初始状态为0。现在进行M次操作，每一次都翻转两个结点的状态。每次操作后，询问：对状态为1的结点之间两两匹配，对匹配点对之间距离进行求和，和的最小值。（显然始终有偶数个状态为1的点）

数据范围：
      N<=100000,M<=100000,time limit:3s,memory limit:512mb.

分析：

      首先考虑最直接的暴力做法。题目要求进行点对的匹配，那么就直接手动搜索所有可能的匹配情况，然后把和最小的方案找出来。直接粘代码，复杂度O(M*sqrt(N!))。

 

      然后考虑比较高效的做法。由于对搜索的做法想不出比较好的优化方法，所以说应该换其他方法，那么需要考虑这个问题的一些特性。首先从简单的情况开始考虑：1、只有两个状态为1的点（以下简称1点），直接匹配；2、有4个1点：

 

      上图是一种比较一般的情况，其中每条边的长度大于等于0。假如我们认为a,b,e,f是我们描述的4个1点，那么显然E(a,c),E(b,c),E(d,e),E(d,f)的长度大于0。由于没有指定长度的相对大小，所以实际上只有两种情况：(1)匹配(a,b),(e,f)，那么距离和为l(a,c)+l(b,c)+l(d,e)+l(d,f)；(2)匹配(a,e),(b,f)，那么距离和为l(a,c)+l(b,c)+l(d,e)+l(d,f)+2*l(c,d)；也就是说无论l(c,d)是否为0，第一种匹配总是不劣于第二种匹配。当l(c,d)大于0，不妨认为d是c的父亲，

     

      由上面分析具有的任意性，得到如下结论：

      当子树中（上图中，c为子树的根）有偶数个结点，在子树中完成这些结点的匹配即可。结果优于子树内结点与其上方子树内结点匹配的结果。

 

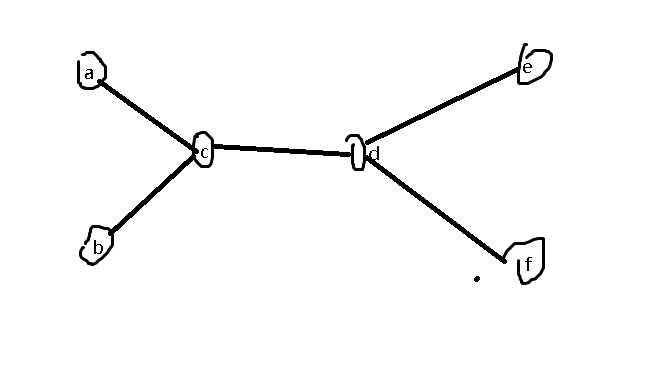
      上面考虑了子树中有偶数个点，接下来考虑奇数个点，构造完整的递归思路：子树中总会有一个结点i要和上方子树内的点进行匹配，除去i之外，子树内剩下偶数个1点，由上得到的结论，它们互相匹配得到最优解。注意，这偶数个点进行匹配时的路径一定经过当前子树的根rt（假如有两个点a1,a2匹配路径不经过rt，说明它们的lca不是rt，递归分析它们应该早就被匹配了）。也就是说对于当前询问结果，rt的子树中所有的1点ai都贡献了dist(ai,rt)。假设rt为1点，那么我们就让rt与上方子树内1点进行匹配；假如rt不是1点，我们在计算完结点i的贡献后，认为结点i为0点，rt为1点，递归到fa[rt]，处理一个等价问题（也就是说运算过程中，某个点是否为1点是依据输入然后按照算法判定的）。

      递归思路已经刻画完成，程序的执行框架不赘述。

      由于每一次询问都要重新计算答案，复杂度O(M*N)。

 

      最后，考虑对第二种做法进行优化：

      假如点i状态发生改变，那么i点会对i->root路径上（包括端点）所有的点“运算过程中是否认定为状态1”都产生影响。声明：接下来的1点定义为以其为根的子树中有奇数个“输入1点”的结点，0点定义则是偶数个。（这是根据第二种方法得到的定义）不难发现当i点的认定状态改变，i->root路径上的所有点（包括端点i,root）的认定状态都会反转，如果i的认定状态为1，那么i会对答案贡献1，反之不贡献。说到这里实际上树剖的做法就自然而然出来了，维护链上的点的认定状态，每一次回答的时候看当前树中认定1点的总数量即可。

      时间复杂度分析：建树剖O(N)，更新O(M*log2n)，单次回答O(1)，回答O(M)，总时间复杂度O(M*log2n)。

 

     AC代码：

  1 #include<iostream>
  2 #include<cstdio>
  3 #include<cstring>
  4 #include<cstdlib>
  5 #include<cctype>
  6 using namespace std;
  7 
  8 int T,N,M,ans;
  9 struct segment_tree{
 10     static const int maxn=100005;
 11     struct edge{ int to,next; }E[maxn<<1];
 12     int np,first[maxn],fa[maxn],son[maxn],sz[maxn],dfs_clock,l[maxn],top[maxn];
 13     int rt,np2,lc[maxn<<1],rc[maxn<<1],c1[maxn<<1];
 14     bool flag[maxn<<1];
 15     void initial(int n){
 16         np=rt=np2=dfs_clock=0;
 17         memset(first,0,sizeof(first));
 18     }
 19     void add_edge(int u,int v){
 20         E[++np]=(edge){v,first[u]};
 21         first[u]=np;
 22     }
 23     void DFS1(int i,int f){
 24         fa[i]=f,son[i]=0,sz[i]=1;
 25         for(int p=first[i];p;p=E[p].next){
 26             int j=E[p].to;
 27             if(j==f) continue;
 28             DFS1(j,i);
 29             if(sz[j]>sz[son[i]]) son[i]=j;
 30             sz[i]+=sz[j];
 31         }
 32     }
 33     void DFS2(int i,int tp){
 34         l[i]=++dfs_clock,top[i]=tp;
 35         if(son[i]) DFS2(son[i],tp);
 36         for(int p=first[i];p;p=E[p].next){
 37             int j=E[p].to;
 38             if(j==fa[i]||j==son[i]) continue;
 39             DFS2(j,j);
 40         }
 41     }
 42     void pushup(int now){
 43         c1[now]=c1[lc[now]]+c1[rc[now]];
 44     }
 45     void Turn(int now,int L,int R){
 46         flag[now]=!flag[now],c1[now]=R-L+1-c1[now];
 47     }
 48     void pushdown(int now,int L,int R){
 49         if(!flag[now]) return;
 50         int m=L+R>>1;
 51         Turn(lc[now],L,m); Turn(rc[now],m+1,R);
 52         flag[now]=0;
 53     }
 54     void build(int &now,int L,int R){
 55         now=++np2,lc[now]=rc[now]=0,c1[now]=0,flag[now]=0;
 56         if(L==R) return;
 57         int m=L+R>>1;
 58         build(lc[now],L,m); build(rc[now],m+1,R);
 59         pushup(now);
 60     }
 61     void update(int now,int L,int R,int A,int B){
 62         if(A<=L&&R<=B){ Turn(now,L,R); return; }
 63         pushdown(now,L,R);
 64         int m=L+R>>1;
 65         if(B<=m) update(lc[now],L,m,A,B);
 66         else if(A>m) update(rc[now],m+1,R,A,B);
 67         else{
 68             update(lc[now],L,m,A,B);
 69             update(rc[now],m+1,R,A,B);
 70         }
 71         pushup(now);
 72     }
 73     void Update(int x){
 74         int tmp=x,cnt0=0,cnt1=0;
 75         while(x){
 76             update(rt,1,N,l[top[x]],l[x]);
 77             x=fa[top[x]];
 78         }
 79     }
 80 }st;
 81 
 82 void data_in()
 83 {
 84     scanf("%d",&N);
 85     st.initial(N);
 86     int x,y;
 87     for(int i=1;i<N;i++){
 88         scanf("%d%d",&x,&y);
 89         st.add_edge(x,y); st.add_edge(y,x);
 90     }
 91     st.DFS1(1,0); st.DFS2(1,1);
 92     st.build(st.rt,1,N);
 93     scanf("%d",&M);
 94 }
 95 void work()
 96 {
 97     int x,y;
 98     for(int i=1;i<=M;i++){
 99         scanf("%d%d",&x,&y);
100         st.Update(x); st.Update(y);
101         printf("%d
",st.c1[st.rt]);
102     }
103 }
104 int main()
105 {
106     scanf("%d",&T);
107     while(T--){
108         data_in();
109         work();
110     }
111     return 0;
112 }

View Code